Test-Bank-for-Heizer-Operations-Management-9e

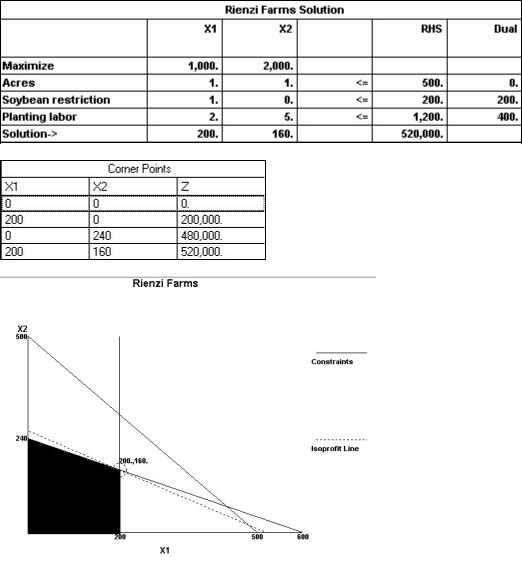
The problem statement is contained in the software panel below. The graphical and corner point solutions are found in the second and third panels. The optimal solution is 200 acres in soybeans and 160 acres in sugar cane. There's not enough labor to plant all 500 acres when 200 acres is in soybeans.

(Graphical solution to a linear programming problem, moderate) {AACSB: Analytic Skills}

521

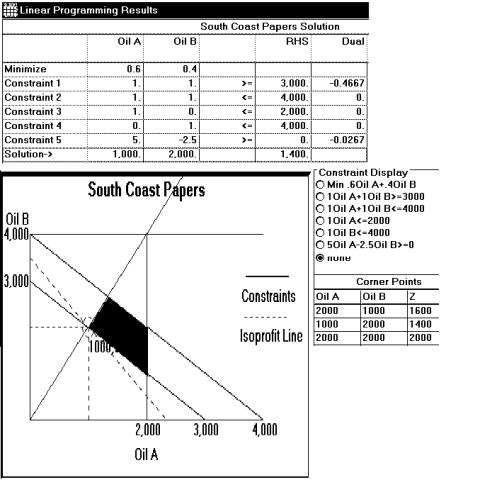
84.South Coast Papers wants to mix two lubricating oils (A and B) for its machines in order to minimize cost. It needs no less than 3,000 gallons in order to run its machines during the next month. It has a maximum oil storage capacity of 4,000 gallons. There are 2,000 gallons of Oil A and 4,000 of Oil B available. The mixed fuel must have a viscosity rating of no less than 40.

When mixing fuels, the amount of oil obtained is exactly equal to the sum of the amounts put in. The viscosity rating is the weighted average of the individual viscosities, weighted in proportion to their volumes. The following is known: Oil A has a viscosity of 45 and costs 60 cents per gallon; Oil B has a viscosity of 37.5 and costs 40 cents per gallon.

State the objective and the constraints of this problem. Plot all constraints and highlight the feasible region. Use your (by now, well-developed) intuition to suggest a feasible (but not necessarily optimal) solution. Be certain to show that your solution meets all constraints.

The problem formulation appears below. The only unusual constraint is the fifth one. This begins as the viscosity expression: viscosity = (45A + 37.5B) / (A + B) ≥ 40, which becomes 5A > 2.5B. It is not possible to meet the restrictions with only Oil A or only Oil B. Most students will discover that a combination is required. They need to show that their mix has a high enough viscosity by substituting their quantities into the viscosity inequality (as well as showing that their quantities are within the four volume constraints).

(Graphical solution to a linear programming problem, difficult) {AACSB: Analytic Skills}

522

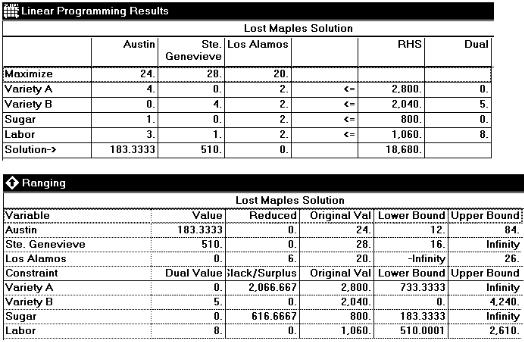
85.Lost Maples Winery makes three varieties of contemporary Texas Hill Country wines: Austin Formation (a fine red), Ste. Genevieve (a table white), and Los Alamos (a hearty pink Zinfandel). The raw materials, labor, and contribution per case of each of these wines is summarized below.

The winery has 2800 bushels of Variety A grapes, 2040 bushels of Variety B grapes, 800 pounds of sugar, and 1060 man-hours of labor available during the next week. The firm operates to achieve maximum contribution. Refer to the POM for Windows panels showing the solution to this problem.

Answer the following questions.

a.For maximum contribution, how much of each wine should be produced?

b.How much contribution will be made by selling the output?

c.Is there any sugar left over? If so, how much? If not, what is its shadow price (dual value)? Explain what this value means to Lost Maples' management.

d.Interpret the meaning of the lower bound to Labor in the Ranging analysis. That is, explain how the solution would change if the amount of labor fell below that lower value.

e.Interpret the meaning of the upper bound to Los Alamos wine in the Ranging analysis.

(a) 183 1/3 cases of Austin Formation, 510 cases of Ste. Genevieve; (b) maximum contribution is $18,680; (c) There are 617 pounds of sugar remaining; its dual value is zero, indication that management should not seek out any more sugar; (d) if the amount of labor fell below the 510 hour level, its dual value would rise; (e) Los Alamos is not currently included in the solution; it would enter the solution only if its contribution rose over the ranging limit of $26 per case.

(Sensitivity analysis, moderate) {AACSB: Analytic Skills}

523

MODULE C: TRANSPORTATION MODELS

TRUE/FALSE

1.The transportation model is an excellent tool for minimizing shipping costs among existing facilities, but it is not useful when firms consider new facility locations.

False (Introduction, easy)

2.The transportation model seeks satisfactory, but not necessarily optimal, solutions for shipping goods from several origins to several destinations.

False (Transportation modeling, moderate)

3.The transportation model is a special class of linear programming models.

True (Transportation modeling, easy)

4.A transportation problem requires exactly as many origins as destinations.

False (Transportation modeling, moderate)

5.Neither the northwest corner rule nor the intuitive method considers shipping cost in making initial allocations.

False (Developing an initial solution, moderate)

6.The intuitive method of generating an initial solution has different results for each problem solver because "intuition" varies from person to person.

False (Developing an initial solution, moderate)

7.The stepping-stone method frequently achieves an optimal solution as soon as it calculates an initial feasible solution.

False (Developing an initial solution, easy)

8.A feasible solution in transportation models is one in which all of the supply and demand constraints are satisfied.

True (Developing an initial solution, moderate)

9.The added cost of shipping one unit through an unused cell in a transportation problem without changing the edge requirements is the shipping cost associated with that cell.

False (The stepping-stone method, moderate)

10.In a transportation minimization problem, the negative improvement index associated with a cell indicates that reallocating units to that cell would lower costs.

True (The stepping-stone method, moderate)

11.Degeneracy in a transportation problem is when no closed path exists for evaluating an unused cell.

True (Special issues in modeling, moderate)

12.When using the stepping stone method, the closed path sometimes has the shape of a triangle as diagonal moves are permitted.

False (The stepping-stone method, moderate)

524

13.When using the stepping stone method for a minimization problem, the number of units that reallocates corresponds to the smallest number found in the cells containing minus signs.

True (The stepping-stone method, moderate)

14.A transportation problem with a total supply of 500 and a total demand of 400 will have an optimal solution that leaves 100 units of supply unused.

True (Special issues in modeling, moderate)

15.A transportation problem with 8 sources and 6 destinations will have an optimal solution that uses at most 13 of the 48 possible routes.

True (Special issues in modeling, moderate) {AACSB: Analytic Skills}

16.To handle degeneracy, a very small quantity is placed in one of the unused squares.

True (Special issues in modeling, moderate)

17.Degeneracy occurs when the number of occupied squares is less than the number of rows plus the number of columns minus one.

True (Special issues in modeling, moderate)

18.If demand exceeds supply in a transportation problem, the problem must be balanced by adding a dummy source with additional supply.

True (Special issues in modeling, moderate)

MULTIPLE CHOICE

19.Which of the following is not needed in order to use the transportation model?

a.the source points and their capacity

b.the fixed costs of source points

c.the destination points and their demand

d.the cost of shipping one unit from each source to each destination

e.All of these are needed.

b (Transportation modeling, easy)

20.The information needs of a transportation problem include

a.the cost of shipping one unit from each origin to each destination

b.the set of destinations and the demand of each

c.the set of origins

d.the supply at each origin

e.all of the above

e (Transportation modeling, easy)

21.Which of the following is not an information need for a transportation problem?

a.the cost of shipping one unit from each origin to each destination

b.the set of destinations and the demand at each

c.the set of origins and the demand at each origin

d.the list of sources and the capacity at each

e.all of the above

c (Transportation modeling, easy)

525

22.The purpose of the transportation approach for location analysis is to minimize

a.total costs

b.total variable costs

c.total fixed costs

d.total shipping costs

e.the number of shipments

d (Transportation modeling, moderate)

23.The transportation method is a special case of the family of problems known as

a.regression problems

b.decision tree problems

c.linear programming problems

d.simulation problems

e.statistical problems

c (Transportation modeling, easy)

24.The initial solution to a transportation problem can be generated several ways, so long as

a.it minimizes cost

b.it ignores cost

c.all supply and demand conditions are satisfied

d.degeneracy does not exist

e.all cells are filled

c (Developing an initial solution, moderate)

25.The northwest corner rule is best used

a.to minimize the total shipping cost from several origins to several destinations

b.to calculate whether a feasible solution is also an optimal solution

c.to calculate how much to transfer from one shipping route to another

d.to generate an initial feasible solution to a transportation problem

e.to resolve cases of degeneracy in transportation problems

d (Developing an initial solution, easy)

26.For the problem data set below, what is the northwest corner allocation to the cell Source 1- Destination 1?

a.0

b.2

c.15

d.30

e.90

c (Developing an initial solution, easy) {AACSB: Analytic Skills}

526

27.For the problem data set below, what is the northwest corner allocation to the cell Source 1 - Destination 2?

a.0

b.15

c.25

d.35

e.45

b (Developing an initial solution, moderate) {AACSB: Analytic Skills}

28.For the problem data set below, what is the northwest corner allocation to the cell Source 3- Destination 3?

a.0

b.15

c.20

d.35

e.45

c (Developing an initial solution, moderate) {AACSB: Analytic Skills}

29.For the problem below, what is the quantity assigned to the cell Source 1-Destination 2 using the intuitive method for an initial feasible solution?

a.1

b.5

c.30

d.45

e.50

d (Developing an initial solution, moderate) {AACSB: Analytic Skills}

527

30.For the problem below, what is the quantity assigned to the cell Source 3-Destination 1 using the intuitive method for an initial feasible solution?

a.3

b.13.333

c.30

d.45

e.50

c (Developing an initial solution, easy) {AACSB: Analytic Skills}

31.A transportation problem has a feasible solution when

a.all of the improvement indexes are greater than or equal to zero

b.all demand and supply constraints are satisfied

c.the number of filled cells is one less than the number of rows plus the number of columns

d.all the squares are used

e.the solution yields the lowest possible cost

b(The stepping-stone method, moderate)

32.A transportation problem has an optimal solution when

a.all of the improvement indexes are greater than or equal to zero

b.all demand and supply constraints are satisfied

c.the number of filled cells is one less than the number of rows plus the number of columns

d.all the squares are used

e.all origin-destination combinations have been made equally low in cost

a (The stepping-stone method, moderate)

33.In transportation model analysis the stepping-stone method is used to

a.obtain an initial optimum solution

b.obtain an initial feasible solution

c.evaluate empty cells for possible degeneracy

d.balance supply and demand

e.evaluate empty cells for potential solution improvements

e(The stepping-stone method, easy)

34.The total cost of the optimal solution to a transportation problem

a.is calculated by multiplying the total supply (including any dummy values) by the average cost of the cells

b.cannot be calculated from the information given

c.can be calculated based only on the entries in the filled cells of the solution

d.can be calculated from the original northwest corner solution

e.is found by multiplying the amounts in each cell by the cost for that cell for each row and then

subtracting the products of the amounts in each cell times the cost of each cell for the columns c (The stepping-stone method, moderate)

528

35.Consider the transportation problem and its optimal solution in the tables below. What is the evaluator for the cell Source 2 – Destination 3?

a.0

b.13

c.17

d.75

e.150

c (The stepping-stone method, moderate) {AACSB: Analytic Skills}

36.Consider the transportation problem and its optimal solution in the tables below. What is the value of the objective function?

a.0

b.$169

c.300 units

d.$2,100

e.$3,140

e (The stepping-stone method, moderate) {AACSB: Analytic Skills}

529

37.Consider the transportation problem and its optimal solution in the tables below. The cell Source 3

–Destination 3 is currently empty. What would be the change in the objective function if the largest possible amount were shipped using that route, leaving all the supply and demand conditions unchanged?

a.0

b.fifty units

c.a decrease of $9

d.an increase of $450

e.an increase of $630

d (The stepping-stone method, difficult) {AACSB: Analytic Skills}

38.Consider the transportation problem and its optimal solution in the tables below. The cell Source 3

–Destination 4 is currently empty. What would be the largest possible amount that could be shipped using that route, leaving all the supply and demand conditions unchanged?

a.0 units

b.5 units

c.30 units

d.50 units

e.90 units

b (The stepping-stone method, moderate) {AACSB: Analytic Skills}

530