1.Основы теории погрешностей

2.Численные методы решения нелинейных уравнений с одним неизвестным

3.Численные методы решения систем линейных уравнений

4.Интерполирование функций

5.Численное дифференцирование

6.Численное интегрирование

7.Численное решение обыкновенных дифференциальных уравнений

1.Основы теории погрешностей

Основные вопросы, рассматриваемые на лекции:

1. Неустранимая погрешность.

2. Ошибки арифметических действий.

3. Основные задачи теории приближённых вычислений.

При решении конкретной задачи источником погрешностей окончательного результата могут быть неточность начальных данных, округления в процессе счета, а также приближённый метод решения. В соответствии с этим будем разделять погрешности на:

1. погрешности из-за начальной информации (неустранимая погрешность);

2. погрешности вычислений;

3. погрешности метода.

1. Неустранимая погрешность

Неустранимая погрешность - это погрешность, связанная с ошибками в исходной информации.  Причинами этих ошибок может быть, например, неточность измерений, невозможность представить данную величину конечной дробью.

Различают абсолютную и относительную погрешности. Пусть x - истинное значение величины, - её приближенное значение, принимаемое в расчетах.  Величина называется абсолютной погрешностью числа .  Точная верхняя грань множества значений , которое определяется найденным , и имеющейся информацией относительно x, называется предельной абсолютной погрешностью величины .  Относительной погрешностью δ величины называется отношение её абсолютной погрешности к величине :  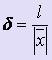 .  Аналогично можно определить предельную относительную погрешность δ _x числа :  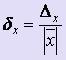  Относительные погрешности чисел принято выражать в процентах, поэтому: 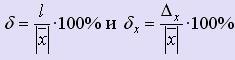   При записи приближённых чисел желательно указывать их точность, сообщая те границы, в которых это число может находиться: ± Δ_x.

Значащая цифра числа считается верной в узком смысле, если абсолютная погрешность (предельная) не превосходит половины единицы того разряда, в котором стоит данная цифра.  В противном случае цифра считается сомнительной.  Значащая цифра числа считается верной в широком смысле, если абсолютная погрешность (предельная) не превосходит единицы того разряда, в котором стоит данная цифра.

При записи чисел руководствуются следующим правилом: все цифры числа должны быть верными.  Поэтому округление чисел, записанных в десятичной системе, производится по правилу первой отбрасываемой цифры:

• Если первая из отбрасываемых цифр меньше 5, то оставляемые десятичные знаки сохраняются без изменения;

• Если первая из отбрасываемых цифр больше 5, то последняя оставляемая цифра увеличивается на 1;

• Если первая из отбрасываемых цифр равна 5, а за ней идут не нули, то последняя оставляемая цифра увеличивается на 1;

• Если первая из отбрасываемых цифр равна 5, и все цифры, идущие за ней - нули, то последняя оставляемая цифра увеличивается на 1, если она нечетная, и остаётся без изменения, если - четная.

 Ошибки арифметических действий

Если f (x, y) = x + y, то Δ_{x + y} = Δ_x + Δ_y.  Если f (x, y) = x - y, то Δ_{x - y} = Δ_x + Δ_y.  Если f (x, y) = x · y, то Δ_xy = .  Если f (x, y) = , то .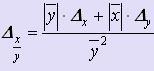

Из формул для абсолютных погрешностей суммы, разности, произведения и частного выводятся формулы для соответствующих относительных погрешностей.       

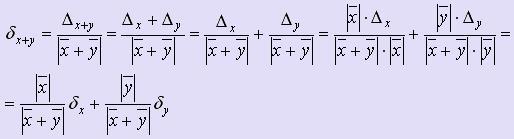
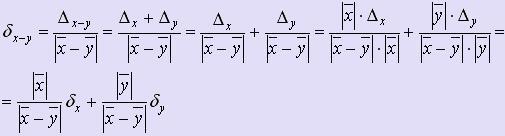
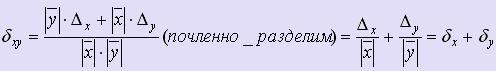
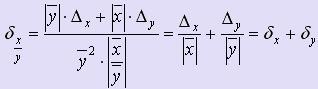
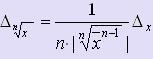Если f (x) = x ⁿ , то Δ_xⁿ = .  Если , то .  δ_xⁿ = n · δ_x.  .

 Основные задачи теории приближённых вычислений

Прямая задача: указаны действия, которые нужно выполнить и заданы предльные погрешности. Требуется оценить погрешность результата.

Обратная задача: указаны действия, которые нужно выполнить, задана погрешность, которая допустима для результата. Требуется установить, какими должны быть погрешности исходных данных, чтобы полученный результат имел заданную точность.