Книга_мат_3_1

type Row = array [ 'a' .. 'c' ] of char;

Таблицю можна розглянути як послідовність трьох рядків і подати масивом типу

type Table = array [ 1 .. 3 ] of Row;

Партія, тобто послідовність позицій, має довжину не більше 9, і може подаватися масивом таблиць:

type Game = array [ 1 .. 9 ] of Table;

Масиви типу Table мають два виміри: номер рядка та номер символу

в ньому; масиви типу Game – три: номери таблиці, рядка та символу. Вимір 1..9 у типі Game називається зовнішнім, вимір 'a'..'c', що нумерує символи в рядках, – внутрішнім.

Тип Game можна задати еквівалентним виразом, не означаючи імен типів Row і Table, а саме:

type Game = array [ 1 .. 9 ] of array [ 1 .. 3 ] of

array [ 'a' .. 'c' ] of char;

Нехай A – змінна типу Game. Вираз вигляду A[ i ], де 1 i 9, задає змінну типу Table, або типу

array [ 1 .. 3 ] of array [ 'a' .. 'c' ] of char;

Мова Паскаль допускає іншу форму задання типів та елементів б а- гатовимірних масивів: виміри та індекси записуються через кому в спільних дужках. Так, означення

type Game1 = array [ 1 .. 9, 1 .. 3, 'a' .. 'c' ] of char

еквівалентне означенню типу Game, а вираз A[i, j, k] – виразові A[i][j][k]. Елементи багатовимірних масивів розташовуються в пам'яті

послідовно, найшвидше в них змінюється внутрішній індекс, найповільніше – зовнішній. Зокрема, двовимірні масиви (матриці) розташовуються за рядками. Так, послідовні числа масиву типу

array [ 1 ..2, 'a' ..'b' ] of real

мають набори індексів [1, 'a'], [1, 'b'], [2, 'a'], [2, 'b'], а послідовні символи в масиві типу Game – [1, 1, 'a'], [1, 1, 'b'], [1, 1, 'c'], [1, 2, 'a'], … , [1, 3, 'c'], [2, 1, 'a'], … , [9, 3, 'c'].

Приклад и використання двомірних масивів

Приклад 12. Скласти програму для розв‟язання системи n лінійних рівнянь з n невідомими.

51

Розв’язання: Задача цікава тим, що вона досить часто постає при розв‟язанні фізичних, технічних, економічних та інших практичних задач. У загальному вигляді система n лінійних рівнянь з n невідомими записується у вигляді:

Двомірний масив, або матриця, утворена з коефіцієнтів біля невідомих, називається матрицею коефіцієнтів даної системи, а одномірний м а- сив, утворений з правих частин рівняння називається порядком системи. Найбільш поширеним алгоритмом розв‟язання систем лінійних рівнянь є алгоритм Гауса, або як його інколи називають – алгоритм виключення невідомих. Пояснимо дію алгоритму на конкретному прикладі, а потім напишемо програму для загального випадку.

Нехай у нас є система трьох рівнянь з трьома невідомими, або іншими словами – дано систему лінійних рівнянь третього порядку.

Хід розв‟язання методом виключення невідомих вам добре відомий з курсу математики, томи ми його просто покажемо. Якщо ж у когось виникнуть труднощі з розумінням ходу розв‟язання, то ми в черговий раз рекомендуємо відкласти в сторону на деякий час даний підручник і засісти за підручник математики.

52

Остання система легко розв‟язується поступовою підстановкою значень змінних від останнього рівняння до першого: х3 = 4, х2 = –2, х1 = 3.

Весь хід нашого розв‟язання можна умовно розбити на дві частини: зведення системи 3-го порядку до рівносильної їй трикутної системи з одиничними коефіцієнтами по діагоналі (цей етап називається прямим ходом алгоритму Гауса), а потім обчислення невідомих, починаючи з кінця (зворотній хід). Зауважимо, що розв‟язання даним методом можливе лише тоді, коли початкова система сумісна і має єдиний розв‟язок.

При програмній реалізації даного алгоритму необхідно врахувати декілька моментів, а саме: на деякому етапі черговий коефіцієнт, що нам потрібно знайти, може бути рівним нулю. Або ж при діленні, яке ми виконуємо постійно, можемо отримати число, яке може виявитись настільки малим, що для нашого електронного друга воно в пам‟яті відображатиметься нулем. Для того, щоб обійти ці невеликі підводні рифи удосконалимо розв‟язання у загальному випадку таким чином, що на кожному че р- говому етапі будемо виключати невідоме з найбільшим за модулем коеф і- цієнтом, іншими словами, ми будемо переставляти рядки матриці (міняти місцями рівняння).

Ми приведемо кінцеву програму алгоритму Гауса з відповідними коментарями у потрібних місцях. Надіємось, що ви вже досягли того рівня класності у програмуванні, коли найбільш прості алгоритми, що використовуються у програмі, вам зрозумілі прямо з тексту програми.

program Gaus; uses dos, crt; const k = 20;

type urawnenie = array[1..k+1] of real; matrix = array[1..k] of urawnenie;

bar = array[1..k] of real; var mas : matrix;

x : bar; max, f : real;

i, j, n, d, l : integer; begin

{ Введення вхiдних даних }

write('Введiть порядок системи: ');readln(n); for i := 1 to n do

begin

for j := 1 to n do begin

write('a[',i,',',j,'] = '); readln(mas[i][j]);

end; write('b[',i,'] = ');

53

readln(mas[i][n+1]); end;

{ Виведення iх на екран у звичному виглядi } writeln('Програма розв''язуе методом Гауса систему: '); for i := 1 to n do

begin

for j := 1 to n+1 do if j < n+1 then

if j = 1 then write(mas[i][j]:2:1,' x',j)

else if mas[i][j] < 0 then write(' - ',-mas[i][j]:2:1,' x',j) else write(' + ',mas[i][j]:2:1,' x',j)

else write(' = ',mas[i][j]:2:1); writeln;

end;

{ Алгоритм Гауса - прямий хiд } for i := 1 to n do

begin

{ вибiр рiвняння з найбiльшим за модулем коеф. при х[i] } max := abs(mas[i][i]);

d := i;

for l := i+1 to n do

if abs(mas[l][i]) > max then begin

max := abs(mas[l][i]); d := l;

end;

{ якщо потрiбно, то переставили мicцями два рiвняння } if d <> i then

for j := i to n+1 do begin

f := mas[i][j]; mas[i][j] := mas[d][j]; mas[d][j] := f;

end;

{ дiлимо i-те рiвняння на коеф. при x[i] } f := mas[i][i];

for j := i+1 to n+1 do mas[i][j] := mas[i][j]/f;

{ виключаемо x[i] з усiх рiвняннь, що стоять нижче } for l := i+1 to n do

begin

{ виключаемо x[i] з l-го рiвняння } f:= mas[l][i];

for j := i+1 to n+1 do mas[l][j] := mas[l][j] - mas[i][j]*f; end;

end;

{ кiнець прямого ходу i початок зворотнього } x[n] := mas[n][n+1];

54

for i := n-1 downto 1 do begin

x[i] := mas[i][n+1];

for j := i+1 to n do x[i] := x[i] - mas[i][j]*x[j] end;

{ виведення результатiв }

writeln; writeln('Коренi системи рiвнянь:'); for i:=1 to n do write(' x[',i,'] = ',x[i]:2:1); readln;

end.

55

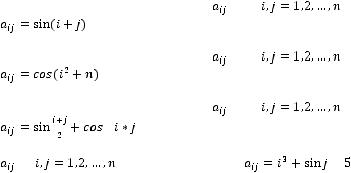
Завдання

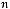
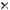
1.Дано цілочислову прямокутну таблицю порядку 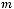. Усі елементи таблиці, менші за середнє арифметичне її значень, замінити на -1, більші – на 1.

2.Дано квадратну дійсну таблицю розмірності n. Обчислити кількість входжень заданого елемента x.

3.Дано квадратну дійсну таблицю розмірності n. Обчислити кількість максимальних елементів.

4.Дано квадратну дійсну таблицю розмірності n. Обчислити кількість мінімальних елементів.

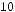
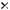
5.Дано прямокутну цілочислову таблицю порядку 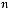. Визначити середнє арифметичне максимального і мінімального її значень.

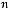
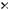
6.Елементи цілочислової прямокутної матриці розміром 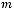задано випадковим чином. Надрукувати пари індексів першого максимального елемента.

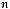
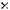
7.Елементи цілочислової прямокутної матриці розміром 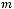задано випадковим чином. Надрукувати пари індексів останнього мінімального елемента.

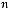
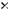
8.Елементи цілочислової прямокутної матриці розміро м 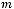задано випадковим чином. Надрукувати пари індексів усіх макс и- мальних елекментів.

9.Дано квадратну дійсну таблицю порядку n. Усі максимальні елементи заданої таблиці замінити нулями.

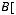
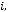
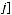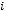
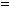
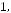
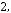
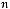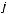
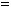
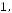
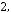
10.Дано таблицю , де , 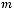. Надрукувати суму елементів кожного стовпчика.

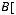
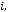
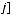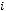
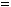
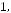
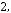
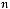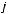
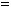
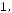
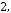
11.Дано таблицю , де , 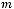. Надрукувати середнє арифметичне кожного стовпчика.

12.Дано натуральне число n. Визначити кількість додатних і кіль-

Контрольні запитання

1. Якими способами задаються елементи матриць?

56

2.Як описуються двохмірні масиви?

3.Які операції застосовують до матричних типів?

57

Лабораторна робота № 11 “Сортування в структурах даних”

Мета: сформувати уміння сортувати дані різних структур.

Питання для вивчення

1.Поняття сортування.

2.Способи сортування:

2.1.сортування методом вставки;

2.2.сортування методом вибору;

2.3.сортування методом обміну.

Теоретичні відомості

Поняття сортування

При розв‟язанні задачі сортування зазвичай висувається вимога м і- німального використання допоміжної пам„яті, із якої витікає недопустимість застосування допоміжних масивів.

Сортування – це розташування інформації в деякій послідовності за

Покращенні методи сортування.

Прямі методи сортування поділяються на три підгрупи: Сортування вставкою Сортування вибором

Сортування обміном ( метод “бульбашок”).

Способи сортування

Сортування вставкою

Принцип методу: масив поділяється на дві частини: відсортовану та не відсортовану. Елементи із не відсортованої частини почергово вибир а- ються й вставляються у відсортовану частину так, щоб не порушити в ній упорядкованість елементів. На початку роботи алгоритму в якості відсо р- тованої частини масиву приймають лише один перший елемент, а в якості не відсортованої частини - всі останні елементи.

Таким чином, алгоритм буде складатися з (n – 1) – го проходу ( n - це розмірність масиву ), кожен з яких буде включати чотири дії:

1.Взяття чергового і – го не відсортованого елемента й збереження її в додатковій змінній;

58

2.Пошук позиції j у відсортованій частині масиву, в якій присутність взятого елемента не порушить впорядкованості елементів;

3.Зсув елементів масиву від (i – 1) - го до (j – 1) – го праворуч, щоб звільнити знайдену позицію вставки;

4.Вставка взятого елемента в знайдену j – у позицію.

Програма, що реалізує розглянутий алгоритм, буде мати такий ви-

гляд:

Program InsertionSort;

Const n=20; { довжина масиву } Type Tvector = array [1. . n] of real; Var Vector : Tvector;

B: real;

i,j, k:integer; Begin

Writeln(„ введіть елементи масиву:‟);

For i:=1 to n do Read( Vector[i] ); Readln;

{ - - - - - - - - - - - - } for i := 2 to n do

begin

B := Vector[i];{взяття не відсортованого елемента} {цикл пошуку позиції вставки}

j := 1;

while ( B > Vector[j] ) do

j := j+1; {після закінчення циклу індекс j фіксує позицію вставки }

{цикл зсуву елементів для звільнення позиції вставки } for k := i – 1 downto j do

Vector[ k+1 ] := Vector [k];

{ вставка взятого елемента на знайдену позицію } Vector [j] := B;

end;

{ - - - - - - - - - - }

writeln („відсортований масив:‟); for i :=1 to n do

write ( Vector [i]:8:2 ); writeln;

End.

Сортування вибором

Принцип метода: знаходимо (вибираємо) в масиві елемент з мінімальним значенням на інтервалі від 1-го елемента до n – го (останнього)елемента і міняємо його місцями з першим елементом. На другому кроці знаходимо елемент з мінімальним значенням на інтервалі від 2 – го

59

до n – го елемента і міняємо його місцями з другим елементом. І так далі для всіх елементів до (n – 1) – го.

Програма, що реалізує метод вибору, буде мати наступний вигляд:

Program SebebionSort;

Begin

Writeln(„ введіть елементи масиву:‟);

For i:=1 to n do

Read( Vector[i] );

Readln;

{ - - - - - - - - - - - - } for s := 1 to n - 1 do begin

{пошук мінімального елемента в діапазоні} {від s- го до n- го елемента} min:=Vector[s];

Imin:=s;

for i := s+ 1 to n do if Vector[i]<min then begin

min:=Vector[i];

Imin:=i;

End;

{обмін місцями мінімального і s - го елементів} Vector[ Imin ] := Vector [s];

Vector [s] := min; End;

{ - - - - - - - - - - }

writeln („відсортований масив:‟); for i :=1 to n do

write ( Vector [i]:8:2 ); writeln;

End.

Сортування обміном

Принцип цього методу полягає в наступному : зліва направо почергово порівнюють два сусідніх елементи, і якщо їх взаємне розташування не відповідає заданій умові впорядкування, то вони міняються місцями. Потім беруться два наступних сусідніх елемента і так далі до кінця мас и- ву.

Після одного такого проходу на останній n - ій позиції масиву буде стояти максимальний елемент ( ”виплила” одна “бульбашка” ).

60