
Книга_мат_3_1
.pdf
1.6.y
1.7.y
1.8.
y
1.9.y
1.10.y
1.11.y
1.12.y
ctgx, |
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
[0; |
], |
|
|
x |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
4x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
2, |
|
в іншому випадку |
|
|
|
20 |
||||||||||||||||||||||||||||||
x2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0, |
|
|
|
|
|
|
|
|
0 |
x |
1 [ |
2; 8], |
|
|
x |
0,25 |
|
|
|
|
|
|
|
||||||||||||||||||
ln x, |
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2x |
|
|
1, |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
cos x, |
|
|
|
|
|
|
|
|
x |
0 |
[ |
5; 5], |
|
|
x |
0,25 |
|
|
|
|
|||||||||||||||||||||
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||
5x , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
|
, |
|
|
|
|
x |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x, |
|
|
0 |
x |
4; |
|
|
[ 2; 8], |
|
|
|
|
|
x |
0,25 |
|
|
|
|
|
|
||||||||||||||||
2, |
|
|
|
|
|
x |
4; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
|
, |
|
|
|
|
|
x |
0; |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
4sin 2x, |
0 |
|
|
|
x |
; |
|
|
|
|
; |
|
|
, |
x |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 |
2 |
|
10 |
|
|
|||||||||||||||||||||||||||||||
0, |
|
|
|
|
|
|
x |
; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 x , |
|
|
|
x |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
cos x, |
|
0 |
|
|
|
x |
|
|
; |
|
|
; |
3 |
|
|
, |
x |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
10 |
|
|
|
||||||||||||
|
2x |
1, |
x |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
1, |
|
x |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
log 2 x, |
1 |
|
|
x |
4; |
0; 5 , |
|
|
|
|
|
x |
0,2 |
|
|
|
|
|
|
|||||||||||||||||||||
2, |
|
|
|
|
|
x |
4; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
41
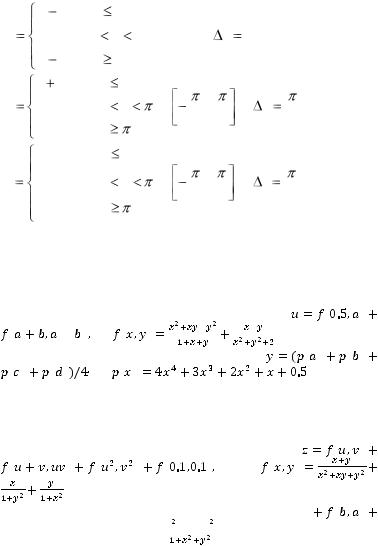
|
|
x |
1, |
|
x |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
1.13. y |
|
log 1 x, |
1 |
x 4; |
[0; 5], |
|
|
x |
|
0,2 |
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
6, |
|
x |
4; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
2, |
|
x |
0; |
|
|
|
|
|
3 |
|
|
|
|
|
|
|||
1.14. y |
|
2cos 2x, |
0 |
x |
; |
|
|
; |
|
|
, |
x |
|
|
|||||||
|
|
|
|
|
|||||||||||||||||
|
2, |
|
|
|
x |
; |
2 |
|
|
2 |
|
|
10 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
, |
|
|
|
x |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.15. y |
2sin |
1 |
x, |
0 |
x |
; |
|
|
; |
|
3 |
|
, |
x |
|
|
|||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
10 |
|
|||||
2x ;
2.Наступну задачу розв‟язати як за допомогою процедури, так і за допомогою функції.
2.1.Написати функцію обчислення суми цифр натурального числа і організувати її виклик для заданих чисел.
2.2. За даними |
дійсними числами a, b обчислити: |
||||||||||||
|
|
|
|
де |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||||
2.3. |
Дано дійсні |
числа |
a, b, c, d. Обчислити: |
||||||||||
|
|
|
|
, де |
. |
||||||||
2.4. |
Дано три довільні числа. Перевірити, чи можна побудувати тр и- |
||||||||||||
|
кутник з такими довжинами сторін. Скласти програму, в якій ви- |
||||||||||||
|
користовується функція для виконання перевірки. Функція по- |
||||||||||||
|
винна повертати значення true або false. |
||||||||||||
2.5. |
Дано дійсні |
числа |
u та v. Визначити значення: |
||||||||||
де
.
2.6. Дано дійсні значення a та b. Обчислити: 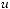
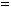
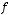
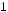

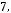

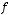

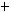
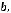
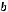


 де
де 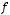
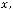
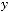
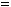

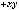
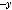 .
.
2.7.Записати підпрограму обчислення факторіалу цілого аргументу, коли відомо, що 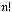
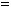
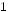

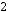



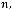 і організувати її виклик для заданого значення n.
і організувати її виклик для заданого значення n.
2.8.Написати функцію обчислення добутку цифр натурального числа і організувати її виклик для заданих чисел.
42

2.9. Дано |
дійсні |
числа х і |
у. |
|
Обчислити: |
|
||||||||||||
|
||||||||||||||||||
|
|
|
|
|
де |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2.10. Дано |
|
дійсні |
числа |
х |
і у. Обчислити: |
|||||||||||||
|
|
|
|
|
де |
|
|
|
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
2.11.Визначити, скільки разів зустрічається цифра “0” в записі чотирьохзначного натурального числа. Скласти програму, в якій використовується функція для підрахування кількості “0” і повертає цю кількість.
2.12.Дано дійсні числа x, y, та z. Обчислити: 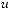
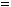

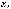
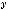
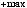
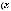
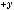
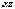
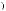 .
.
2.13. Дано |
дві трійки чисел a1, b1, c1, |
a2, b2, |
c2. Обчислити вирази |
||
S |
max a1 ,b1 , c1 |
max a2 ,b2 , c2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2.14. Дано |
дві трійки чисел a1, b1, c1, |
a2, b2, |
|
c2. Обчислити вираз |
|
d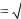 min a1 ,b1 ,c1 min a2 ,b2 ,c2
min a1 ,b1 ,c1 min a2 ,b2 ,c2
2.15.Дано дійсні числа a,b, c. Обчислити: 
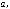
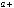
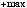
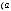

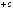
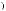 .
.
Контрольні запитання
1.Які дії виконує оператор процедури?
2.Який вигляд має структура опису процедури та функції? У чому відмінність між ними?
3.Що таке область дії ідентифікаторів? Як визначають область дії для ідентифікаторів процедур та функцій?
4.Які параметри називають формальними, а які – фактичними? За якими ознаками їх розрізняють?
5.Які є способи передавання параметрів?
6.Які змінні називають локальними? Який час життя та область дії таких змінних?
7.Які змінні називають глобальними? Який час життя та область дії таких змінних?
8.В яких розділах пам‟яті зберігаються локальні змінні, а в яких – глобальні?
9.Як описати змінну процедурного типу?
Лабораторна робота № 8 “Рекурсія”
Мета: сформувати уміння програмування з рекурсивними обрахунками.
Питання для вивчення
43
1.Рекурсивні процедури і функції.
2.Механізм рекурсивних обчислень.
Теоретичні відомості
Рекурсивні процедури |
і функції |
З поняттям допоміжної підпрограми |
пов‟язане більш складне по- |
няття рекурсивної підпрограми – підпрограми, яка використовує в якості допоміжної саму себе.
Рекурсивні підпрограми обчислення функцій за зовнішньою фо р- мою виглядають так само, як і звичайні. Головна особливість рекурсивної підпрограми – виклики цієї ж підпрограми в процесі її виконання, тобто виклики підпрограми самої з себе ще до закінчення попереднього виконання. Тобто робота підпрограми в певний момент призупиняється, пр о- міжні результати зберігаються, і розпочинається його повторне виконання з іншими значеннями аргументів. Під час повторного виконання підпро г-
рама може знову викликати себе саму. Такий процес викликів називається розгорткою рекурсії. Очевидно, що він не може тривати нескінченно.
Процес припиняється при певних граничних значеннях аргументів . Після цього починається згортка рекурсії: останнє обчислене значення функції підставляється у вираз передостатнього виконання і т. д.
Рекурсивна підпрограма повинна мати перевірку значень аргуме н-
тів, при яких припиняються рекурсивні виклики.
Рекурсивне визначення – спосіб задання функцій, при якому значення шуканої функції в заданій точці визначається через її значення в попередніх точках. Воно дозволяє з допомогою кінцевого висловлення визначити нескінченну множину об‟єктів. З допомогою кінцевої рекурсивної програми можна описати нескінченне обчислення, крім того прогр а- ма не буде містити явних повторень.
Підпрограма, яка звертається сама до себе як до підпрограми (бе з- посередньо або через ланцюг підпрограм ), називається рекурсією.
Для вираження рекурсивних програм необхідно і досить мати поняття процедури або підпрограми, оскільки вони дозволяють дати довільному оператору ім ‟я, з допомогою якого до нього можна звертатися. Саме слово “рекурсія” означає “повернення”.
Приклад 9. Дано ціле невід‟ємне число n; знайти n!. Використовувати програму, яка включає рекурсивну підпрограму.
uses crt; |
|
const n=5; |
{n від 0 до 20} |
function factorial(n:byte): comp; begin
if n=0 then factorial:=1
else factorial := factorial(n-1)*n end;
44
BEGIN
Write(n,”!= “,factorial(n):0:0);
Readln
END.
Роботу рекурсивної функції розглянемо на прикладі обчислення 5!. За означенням 5!=4!*5. Таким чином, щоб обчислити 5! ми повинні споч а- тку обчислити 4!. Використовуючи означення ще раз, знаходимо, що 4!=3!*4, тобто треба обчислити 3!. Продовжуючи процес, одержимо
5!=4!*4; 2) 4!=3!*4; 3) 3!=2!*3; 4) 2!=1!*2; 5) 1!=0!*1; 6) 0!=1.
У кроках 1)-5) завершення обчислення кожен раз відкладається, а шостий крок є ключовим. Одержали значення, яке визначається безпос е- редньо, а не як факторіал другого числа. Тобто ми можемо повернутися від 6) до 1), послідовно використовуючи значення, що обчислюються: 5‟) 1!=1; 4‟) 2!=2; 3‟) 3!=6; 2‟) 4!=24; 1‟) 5!=120.
Рекурсивний виклик процедури мало чим відрізняється від виклику іншої процедури. Схематично внутрішній механізм рекурсії виглядає так:
1)розміщуються в пам‟яті параметри, які передаються процедурі;
2)зберігаються в пам‟яті значення внутрішніх змінних;
3)запам’ятовується адреса повернення до процедури, яка викликається;
4)передається керування викликаній процедурі.
Врекурсивних підпрограмах можна виділити дві серії кроків. Перша
серія – це кроки рекурсивного заглиблення підпрограми в себе до тих пір,
поки вибраний параметр не досягне граничного значення. Кількість таких кроків називається глибиною рекурсії. Друга серія – це кроки рекурсивного
виходу до тих пір, поки обраний параметр не досягне початкового значе н- ня. Вона забезпечує отримання проміжних і кінцевих результатів.
Механізм рекурсивних обчислень
Рекурсія є узагальненням цикла. Приклад демонструє заміну цикла рекурсією. Цього слід уникати так як рекурсії потребують додаткової пам‟яті.
Приклад 10. Рекурсія – узагальнення циклу.
Var i,s1,s2:byte;
Procedure iter;
Begin
While i<55 do
Begin
Inc(i); inc(s1,sqr(i))
End;
End;
45
Procedure rec; Begin
If i<5 then Begin
inc(i); inc(s2,sqr(i)); rec; End;
End; BEGIN
I:=0; s1:=0; iter; I:=0; s2:=0; rec;
Write(s1=s2); readln END.
Завдання
Скласти програму з використанням рекурсії до завдань лаборато р- ної роботи №6.
Контрольні питання
1.Який об‟єкт називають рекурсивним?
2.В чому полягає потужність рекурсивних означень?
3.У чому переваги та недоліки застосування рекурсивних процедур у порівнянні з нерекурсивними?
4.Що таке “глибина” рекурсії?
5.Що таке поточний рівень рекурсії?
6.Яка головна вимога до рекурсивних процедур?
7.Яких форм може набувати структура рекурсивної процедури?
46
Лабораторна робота № 9 “Одновимірні масиви”
Мета: сформувати поняття одновимірного масиву, відпрацювати вміння і навички використання одновимірних масивів та виконання дій над елементами масиву при розв‟язуванні задач.
Питання для вивчення
1.Поняття одновимірного масиву.
2.Операції над масивами.
3.Операції над елементами масиву
Теоретичні відомості
Поняття одновимірного масиву
Масив - це сукупність скінченої кількості даних одного типу. Позначається масив одним іменем.
Кожен елемент масиву позначається іменем масиву з індексом. Кількість елементів масиву фіксується при описі масиву і в процесі виконання програми не змінюється.
Масив називається лінійним (одновимірним), якщо для отримання доступу до його елементів достатньо однієї індексної змінної. Наприклад: a[1], a[2], …, a[n] – масив “a”, який містить “n” елементів.
В пам‟яті ПК елементи масиву слідують один за одним в спеціально відведеній для цього області, яку ми резервуємо при описі. Розміри цієї області залежать від типу, яким ми описуємо дані масиву (byte, integer, real і т.д.). Чим більший тип, тим більше місця виділяється в пам ‟яті.
Опис масивів
1 спосіб
var ім‟я_масиву: array[поч_індекс..кін_індекс] of тип_даних;
Наприклад, A: array[1..6] of integer;
A, D, B: array[1..10] of real;
2 спосіб
type ім‟я_типу=array[поч_індекс..кін_ індекс] of тип_даних; var ім‟я_масиву:ім‟я_типу;
Наприклад, type mas=array[1..10] of real; Var a:mas;
Для опису масивів можна використовувати попередньо визначені константи, якщо невідома кількість елементів масиву.
Const n=50;
Var a:array[1..n] of integer;
Операції над масивами
Для роботи з цілими масивами використовуються імена без індексів: 1) дія: A=B або A<>B - порівняння двох однотипних масивів з однако-
47
вою кількістю елементів; 2) дія: X:=A - всі значення елементів масиву A присвоюються відповідним елементам масива X.
Елементи масиву називаються індексованими змінними і використовуються також як прості змінні.
Елементи масиву вводяться в пам ‟ять комп‟ютера з клавіатури за
допомогою оператора read (readln) в циклі:
For i:=1 to 20 do Readln(a[i]);
Елементи масиву виводяться на екран за допомогою оператора write
(writeln) в циклі:
For i:=1 to 20 do Write(a[i],‟,‟); - в рядок; For i:=1 to 30 do Writeln(a[i]);
Перегляд елементів масиву здійснюється за допомогою циклів. Пошук елементів масиву за деякою ознакою здійснюється за допомогою опе-
ратора if-then в режимі перегляду:
For i:=1 to 10 do Begin
If a[i]=0 then …
Перестановка елементів масиву здійснюється за допомогою додат-
кової змінної:
X:=A[3];
A[3]:=A[1];
A[1]:=X;
Приклад 11. Підрахуйте кількість додатних елементів лінійної таблиці
A[1..10], |
яка складається з цілих чисел. |
|
|
Program pr1; |
|
||
Type |
mas=array[1..10] of integer; |
|
|
Var |
a:mas; |
|
|
|
I, k:integer; |
|
|
Begin |
|
|
|
Clrscr; |
|
|
|
Writeln(„Введіть елементи масиву:‟); |
|
||
For i:=1 to 10 do |
{ініціалізація масиву} |
||
Readln(a[i]); |
|
||
K:=0; |
{кількість додатнихелементів} |
||
For i:=1 to 10 do |
|
||
If a[i]>0 |
then k:=k+1; |
|
|
Writeln(„Кількість додатнихелементів масиву=„, k);
Readln
End.
48
Завдання
1.Задані натуральне число n і послідовність дійсних чисел a1, a2,…, an. У заданій послідовності визначити кількість сусідств двох додатних чисел.
2.Задані натуральне число n і послідовність дійсних чисел a1, a2,…, an. У заданій послідовності визначити кількість сусідств двох чисел різного знака.
3.Дано масив цілих чисел. Знайдіть різницю найбільшого та найменшого чисел.
4.Вихідними даними є цілочисельна таблиця “температура”[1..31], в якій записана температура за кожен день січня, і величина s, яка рівна сер е- дній температурі в січні за останнє століття. Підрахувати, скільки в с і- чні було днів з температурою, більшою, меншою та рівною середній.
5.Дана цілочисельна таблиця. Знайти кількість елементів цієї таблиці, більших за середнє арифметичне всіх її елементів.
6.Задані натуральне число n і послідовність дійсних чисел a1, a2,…, an. У заданій послідовності визначити кількість сусідств трьох нульових членів.
7.Нехай дано натуральне число n і послідовність попарно різних дійсних чисел a1, a2,…, an. У даній послідовності поміняти місцями найбільший член з першим по порядку (якщо їх індекси збігаються – повідомити про це).
8.Нехай дано натуральне число n і послідовність попарно різних дійсних чисел a1, a2,…, an. У даній послідовності поміняти місцями найменший член з останнім по порядку (якщо їх індекси збігаються – повідомити про це).
9.Нехай дано натуральне число n і послідовність попарно різних дійсних
чисел a1, a2,…, an. У даній послідовності поміняти місцями найбільший
і найменший члени.
10.В масиві цілих чисел потрібно замість і-го елемента записати суму чисел від a[1] до a[i] включно і вивести на екран.
11.N точок задано своїми координатами на площині: масив X містить абсциси точок, масив Y - ординати (Ai(x[i], y[i])). Знайти дві точки, відстань між якими найбільша.
12.Дано масив цілих чисел. Визначити, чи є в масиві два нульових членів, розташованих підряд.
13.Нехай дано натуральне число n і послідовність попарно різних дійсних чисел a1, a2,…, an. У даній послідовності поміняти місцями найменший член із членом, що стоїть на k-му місці.
14.Дано два масиви, що складаються з однакової кількості цілих елементів. Отримати третій масив тієї ж розмірності, кожний елемент якого дорівнює більшому з відповідних елементів даного масива.
49
15.Дано одновимірний масив. Переставити у зворотньому порядку елем е- нти масива, які розташовані між мінімальним та максимальним елем е- нтами.
Контрольні запитання
1.Що таке лінійний масив?
2.Як позначається масив і якими параметрами визначаються елементи масиву?
3.Чи можна змінювати розмірність або кількість елементів масиву під час виконання програми? Чому?
4.Які ви знаєте способи опису масивів?
5.Які ви знаєте дії над масивами?
6.Які дії можна виконувати над елементами масиву?
7.Що робить компілятор, коли зустрічає такий опис: var a:array[1..6] of real?
8.Як розташовані елементи масиву в пам ‟яті комп‟ютера?
Лабораторна робота № 10 “Двовимірні масиви або матриці”
Мета: cформувати поняття про матриці та основних операцій, що виконуються над матрицями, навчити розв‟язувати задачі.
Питання для вивчення
1.Способи описання матриць у Паскалі.
2.Приклади використання двомірних масивів.
Теоретичні відомості
Способи описання матриць у Паскалі
Розглянемо прямокутну таблицю з m n однотипиних елементів як послідовність із m рядків, у кожному з яких n елементів. Послідовності
певної довжини подаються в мовах програмування масивами. Отже, виникає поняття "масив, елементами якого є масиви", або двовимірний масив.
Якщо елементи прямокутної таблиці самі є послідовностями або таблиці утворюють послідовність певної довжини, то виникає поняття тривимірного масиву тощо.
Означення багатовимірних масивів та зображення їх елементів у мові Паскаль опишемо за допомогою простого прикладу. Позиція в грі "хрестики-нулики на полі 3 3" подається квадратною таблицею з символів 'x', '0' або ' ' (пропуск). Пронумеруємо клітинки поля, як у шахах – літерами 'a', 'b', 'c' по горизонталі та числами 1, 2, 3 по вертикалі. То ді рядки таблиці можна подати масивами типу
3" подається квадратною таблицею з символів 'x', '0' або ' ' (пропуск). Пронумеруємо клітинки поля, як у шахах – літерами 'a', 'b', 'c' по горизонталі та числами 1, 2, 3 по вертикалі. То ді рядки таблиці можна подати масивами типу
50
