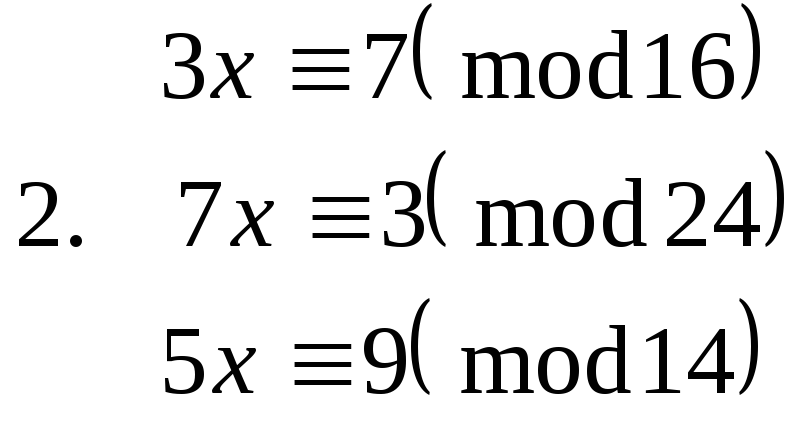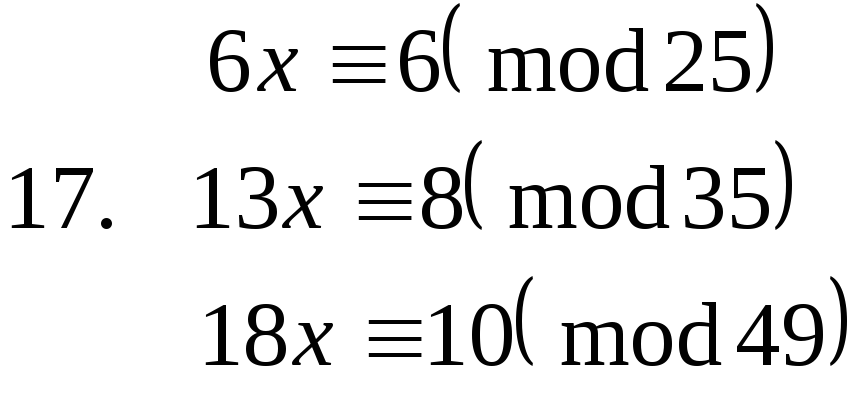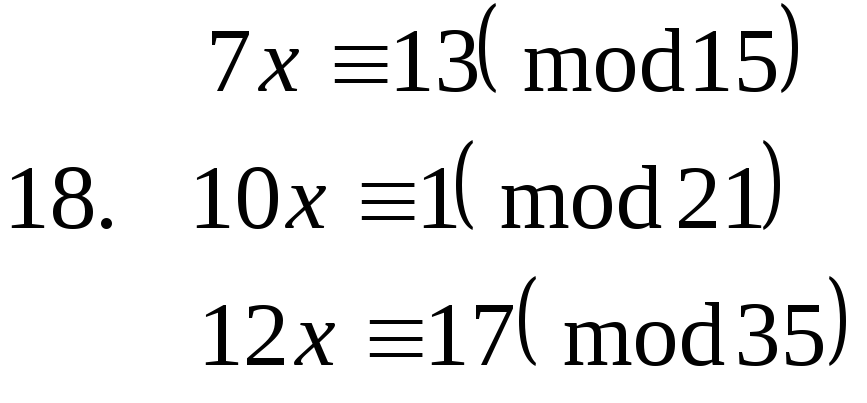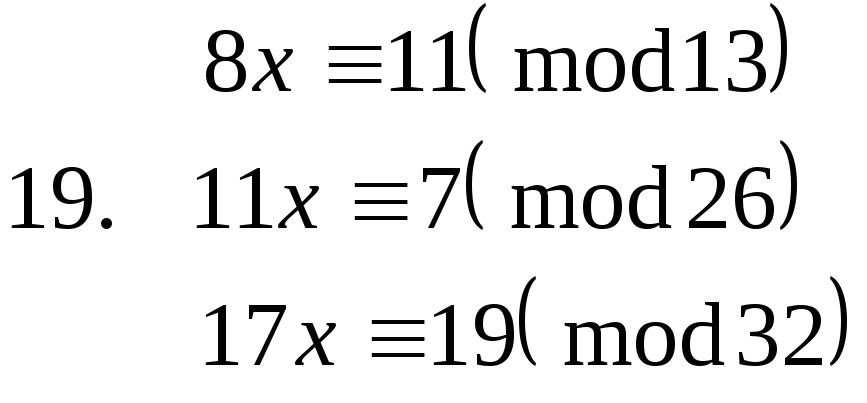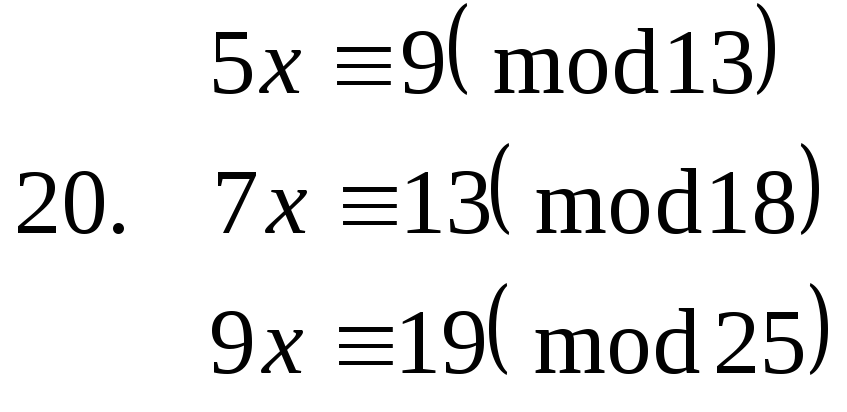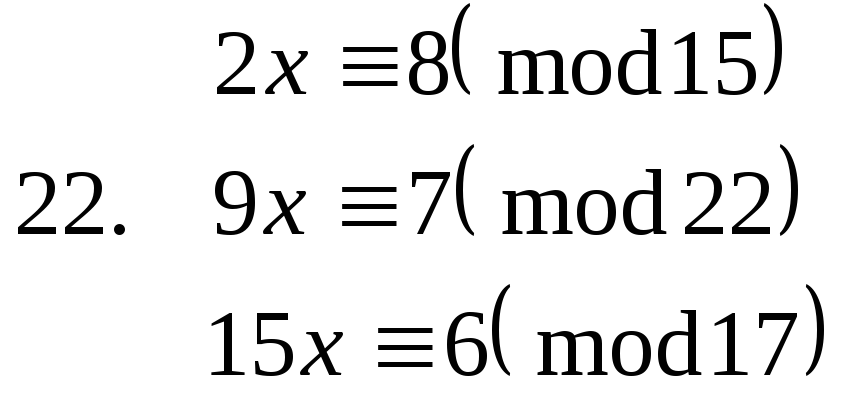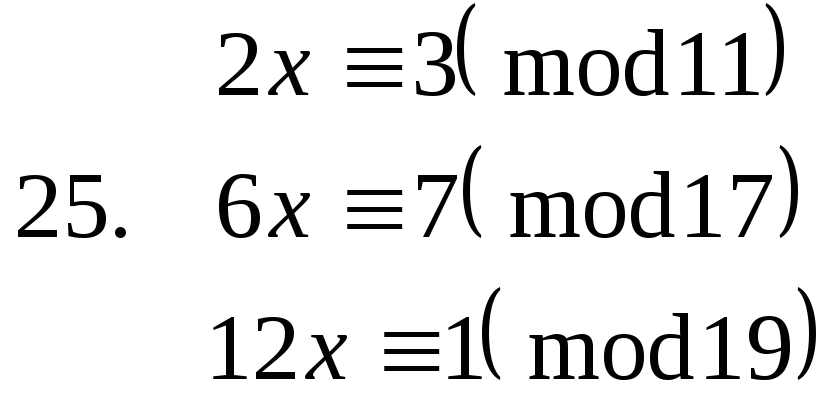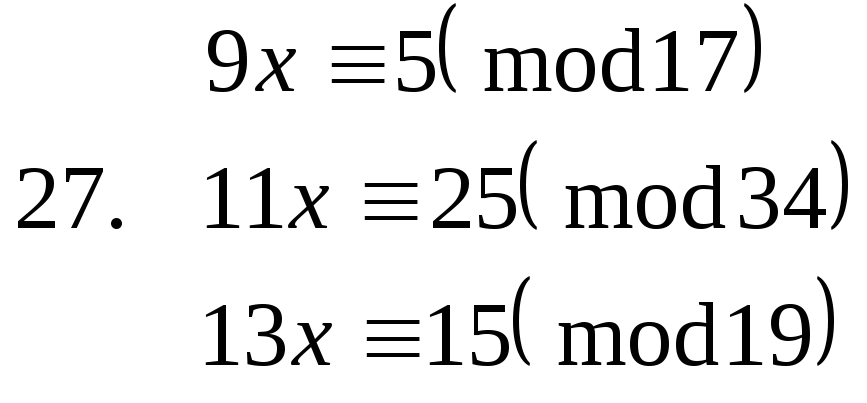- •Індивідуальні завдання з теорії чисел з методичними рекомендаціями до виконання
- •§1. Подільність чисел. Метод математичної індукції.
- •§ 2. Алгоритм Евкліда. Найбільший спільний дільник і найменше спільне кратне
- •§ 3. Систематичні числа.
- •§ 4. Прості числа
- •§ 5. Ланцюгові дроби.
- •§ 6. Функція Ейлера
- •§ 7. Основні властивості конгруенцій.
- •§8. Ознаки подільності.
- •§9. Теореми Ейлера і Ферма.
- •§ 10. Конгруенції першого степеня з однією невідомою.
- •§ 11. Невизначені рівняння першого степеня.
- •§ 12. Системи конгруенцій першого степеня.
- •§ 13. Конгруенції другого степеня за простим модулем.
- •§ 14. Порядок числа. Первісні корені.
- •§ 15. Індекси та двочлени конгруенції.
- •§ 16. Довжина періоду десяткового дробу.
§8. Ознаки подільності.
В
шкільному курсі математики знайомляться
з ознаками подільності на числа
![]() Ознака подільності на число
Ознака подільності на число![]() :
число ділиться на
:
число ділиться на![]() тоді і тільки тоді, коли різниця між
сумою цифр, які стоять на парних місцях,
і сумою цифр, які стоять на непарних
місцях, ділиться на
тоді і тільки тоді, коли різниця між
сумою цифр, які стоять на парних місцях,
і сумою цифр, які стоять на непарних
місцях, ділиться на![]() .
.
Аналогічно
формулюється ознака подільності на
![]()
/отже,
на
![]() і
і![]() ,
так як
,
так як![]() /.
Дане число потрібно записати в системі
числення з основою
/.
Дане число потрібно записати в системі
числення з основою![]() ,
тобто розбити цифри даного числа на
групи по три цифри справа наліво. Ряд
ознак подільності можна отримати, якщо
скористатися тією властивістю, що
число, яке ділиться на взаємно прості
числа, ділиться на добуток отанніх.
,
тобто розбити цифри даного числа на
групи по три цифри справа наліво. Ряд
ознак подільності можна отримати, якщо
скористатися тією властивістю, що
число, яке ділиться на взаємно прості
числа, ділиться на добуток отанніх.
Приклад.
Знайти значення цифр
![]() та
та![]() ,
які задовільняють умову
,
які задовільняють умову![]() .
.
Так як
![]() ,
то
,
то![]() А так як
А так як![]() то
то![]()
Отже,
![]()
Відповідь:
![]()
Завдання.
Знайти
значення цифр
![]() та
та![]() ,
які задовільняють вказані умови.
,
які задовільняють вказані умови.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
§9. Теореми Ейлера і Ферма.
Теорема
Ейлера.
При натуральному
![]() взаємно простому з цілим числом
взаємно простому з цілим числом![]() має місце порівняння
має місце порівняння![]() .
.
Теорема
Ферма. Якщо
ціле число
![]() не ділиться на просте число
не ділиться на просте число![]() ,
то
,
то![]() .
.
Приклад.
Знайти
натуральні значення
![]() ,
які не перевищують
,
які не перевищують![]() і задовільняють порівнянню
і задовільняють порівнянню![]() .
.
Так як
![]() ,
то
,
то![]()
Так як
![]() то
то![]()
Відповідь.
![]()
Завдання.
Знайти
всі натуральні значення
![]() ,
які не перевищують
,
які не перевищують![]() і завільняють порівняння
і завільняють порівняння![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
§ 10. Конгруенції першого степеня з однією невідомою.
Конгруенція
виду
![]() ,
де
,
де![]() ,
має єдиний розв’язок
,
має єдиний розв’язок![]()
Часто
при розв’язанні такої конгруенції
використовують апарат ланцюгових
дробів. Нехай
![]() та
та![]() .
Тоді
.
Тоді![]() .
.
Конгруенція
![]() не має розв’язків якщо
не має розв’язків якщо![]() і
і![]() .
.
Якщо
![]() і
і![]() ,
то конгруенція має
,
то конгруенція має![]() розв’язків
розв’язків![]() ,
де
,
де![]() -
розв’язок допоміжної конгруенції
-
розв’язок допоміжної конгруенції
![]() .
.
Приклад.
Розв’язати
конгруенцію
![]()
Так як
![]() ,
то конгруенція має один розв’язок.
Розкладемо
,
то конгруенція має один розв’язок.
Розкладемо![]() в ланцюговий дріб;
в ланцюговий дріб;![]() .
Потім знаходимо, що
.
Потім знаходимо, що![]() .
Отже,
.
Отже,![]() .
.
Відповідь:
![]() .
.
Завдання. Розв’язати конгруенції першого степеня з однією невідомою.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
§ 11. Невизначені рівняння першого степеня.
Невизначене
рівняння
![]() при
при![]() і
і![]() не має розв’язків. Якщо ж
не має розв’язків. Якщо ж![]() і
і![]() ,
то розв’язки рівняння задаються
формулами
,
то розв’язки рівняння задаються
формулами![]() де
де![]() - розв’язок конгруентності
- розв’язок конгруентності![]() і
і![]() - ціле число.
- ціле число.
Приклад.
Розв’язати
невизначене рівняння
![]()
Так як
![]() і
і![]() ,
то рівняння має нескінченну множину
розв’язків. Розв’язуючи допоміжну
конгруентність,
,
то рівняння має нескінченну множину
розв’язків. Розв’язуючи допоміжну
конгруентність,![]() або
або![]() знаходимо,
що
знаходимо,
що![]() Тоді
Тоді![]()
Відповідь.
![]()
Завдання. Розв’язати невизначені рівняння.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
§ 12. Системи конгруенцій першого степеня.
Для сумісності системи конгруенцій
![]()
![]()
-------------------
![]()
необхідно, щоб кожна конгруенція мала розв’язок.
Розв’язуючи
першу конгруенцію знаходять, що
![]() або
або![]() - ціле
число. Знайдене значення
- ціле
число. Знайдене значення![]() підставляють в другу конгруенцію:
підставляють в другу конгруенцію:![]() Якщо
Якщо![]() то
то![]() і
і![]() або
або![]() Отримане значення
Отримане значення![]() ,
яке задовільняє перші дві конгруенції,
підставляють в третю конгруенцію і так
далі. Якщо система
,
яке задовільняє перші дві конгруенції,
підставляють в третю конгруенцію і так
далі. Якщо система![]() сумісна, то розв’язками будуть класи
чисел по модулю
сумісна, то розв’язками будуть класи
чисел по модулю![]() ,
де
,
де![]() .
.
Приклад. Розв’язати систему конгруенцій.

Конгруенція
![]() має розв’язок
має розв’язок![]()
![]() .
Якщо
.
Якщо![]() то
то![]() або
або![]() ,
звідки
,
звідки![]() .
.
Підставляючи
значення
![]() в третю конгруенцію, отримаємо:
в третю конгруенцію, отримаємо:![]() .
Підстановка інших значень
.
Підстановка інших значень![]() в третю конгруенцію не дає нічого
нового. Якщо
в третю конгруенцію не дає нічого
нового. Якщо![]() то приходимо до конгруенції
то приходимо до конгруенції![]() ,
яка не має розв’язків.
,
яка не має розв’язків.
Відповідь.
![]() .
.
Завдання. Розв’язати конгруенції першого степеня.