Індивідуальні завдання з теорії чисел з методичними рекомендаціями до виконання

для студенті спеціальностей „Математика та основи інформатики”, „Математика та фізика”,

„Інформатика” , „Статистика”

§1. Подільність чисел. Метод математичної індукції.

Якщо для цілих чисел і існує таке ціле , що , то називається дільником числа . Також говорять, що ділиться на або  кратне або ділить . Для позначення подільності числа на користуються символом .

Мають місце наступні теореми про подільність:

Виконуються теореми обернені першій.

Розв’язання вправ методом математичної індукції вимагає використання аксіоми індукції:

Приклад.

Довести, що при будь-якому натуральному n

Розглянемо множину

a)

б) ,

але

Так як за припущенням, то і одержана сума ділиться на.

За умовою аксіоми індукції є множиною всіх натуральних чисел, отже, при будь-якому натуральному

Завдання

Довести, що при будь-якому натуральному мають місце слідуючі твердження

§ 2. Алгоритм Евкліда. Найбільший спільний дільник і найменше спільне кратне

Має місце теорема про ділення з остачею:

Процес послідовного ділення числа на число, потім числана остачу, отриману при першому діленні, потім остачу на остачу, отриману при другому діленні і т.д. називають алгоритмом Евкліда, застосованим до чиселі.

Найбільше натуральне число, на яке діляться числа і, називається найбільшим спільним дільником цих чисел.

Найменше натуральне число, яке ділиться на числа іназивається найменшим спільним кратним цих чисел.

Найбільший спільний дільник чисел іпозначають черезабо НСД, а найменше спільне кратне -або НСК.

При застосуванні алгоритму Евкліда до чисел іостання відмінна від нуля остача дорівнює найбільшому спільному дільнику цих чисел.

Мають місце теореми:

Приклад.

Знайти

Спочатку знаходимо

Так як

то

Тоді за умови теореми отримаємо.

Завдання.

Знайти найбільший спільний дільник або найменше спільне кратне чисел, застосовуючи алгоритм Евкліда.

§ 3. Систематичні числа.

Представлення натурального числа у вигляді

де

називається представленням числа в системі числення з основою. Числаназиваються цифрами числа. Використовується коротший запис числав системі числення з основою

Щоб представити число в системі числення з основоюділятьна

потім на

і так далі ділять на

Легко переконатися в тому, що

Так виконується перехід від десяткової системи до системи числення з основою .

Щоб зв’ясувати, представленням якого натурального числа є дане , потрібно перейти від скороченого запису числа до повного і виконати вказані операції. Тим самим буде здійснений перехід від недесяткової системи числення до десяткової.

Перехід від недесяткової системи числення до недесяткової здійснюється в два етапи: спочатку від недесяткової переходять до десяткової, а потім від десяткової до потрібної недесяткової системи числення.

Інколи остання задача вирішується шляхом безпосереднього ділення в системі числення з основою даного представлення числа на нову основу/попередньо необхідно представити в системі числення з основою/.

Приклад.

Розв’язати рівняння

Спосіб 1. Переходимо до системи числення з основою :

Потім переходимо до системи числення з основою

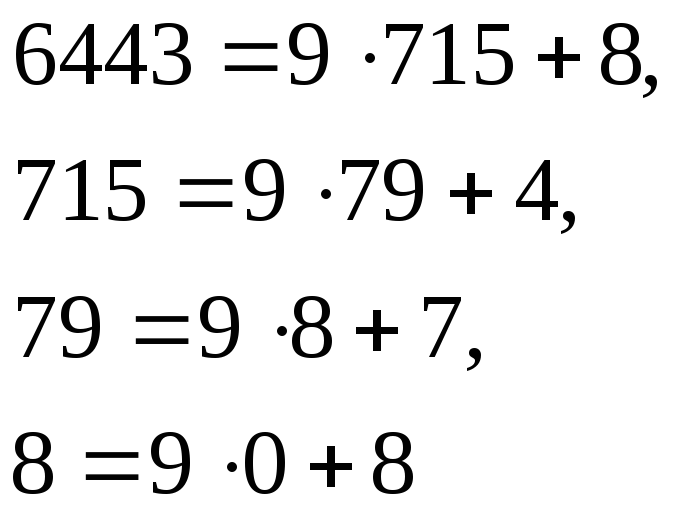
Відповідь:

Спосіб 2. В цьому випадку , а

Ділення виконуємо в системі числення з основою

Так як і, то

Завдання. Розв’язати слідуючі рівняння: