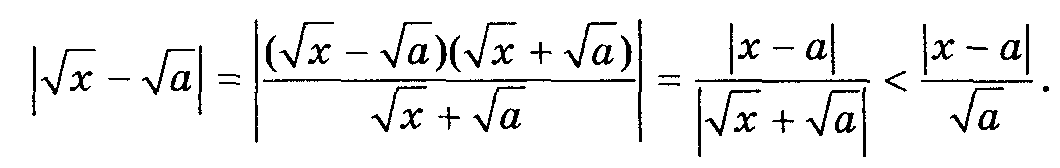Розв'язання
а) Доведемо, що 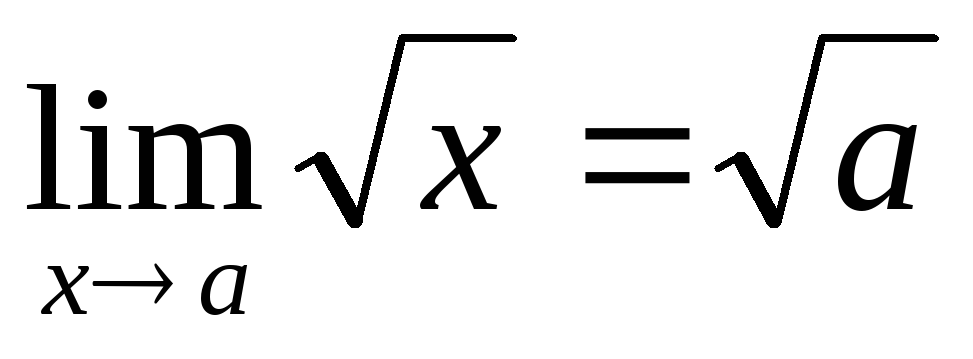 при а > 0.
при а > 0.
Оцінимо різницю
 –
–
 :
:
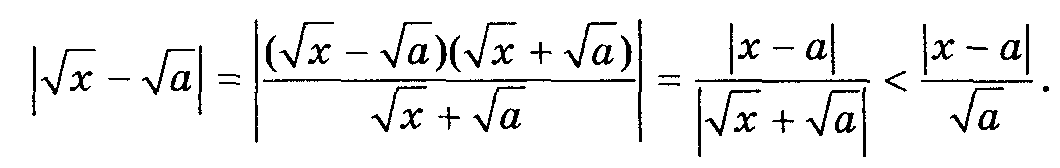
Легко бачити:
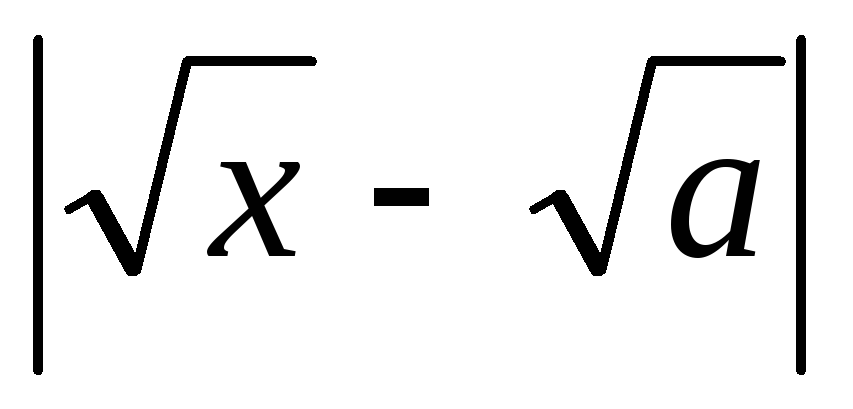 <
ε, ε > 0,
якщо взяти
<
ε, ε > 0,
якщо взяти 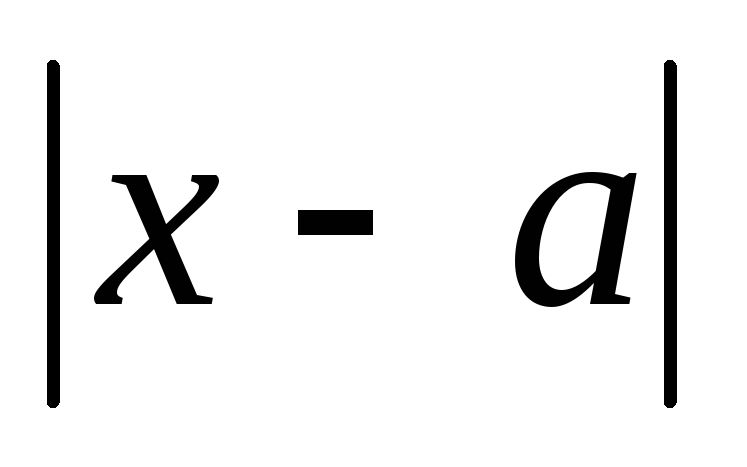 менше
менше
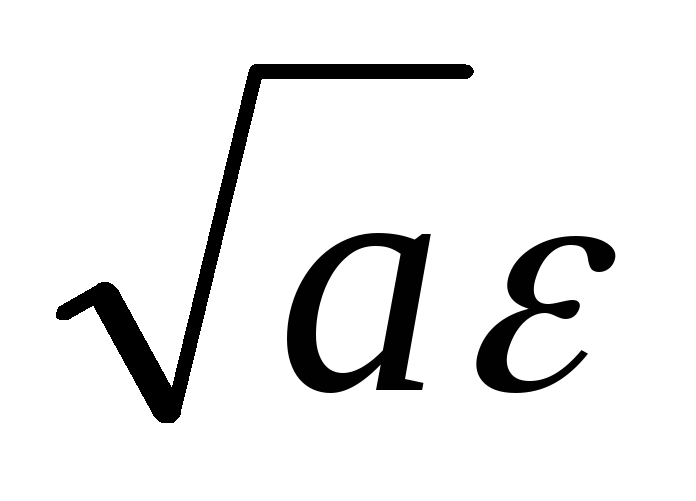 .
Таким
чином, для всякого
ε > 0 існує
δ =
.
Таким
чином, для всякого
ε > 0 існує
δ =
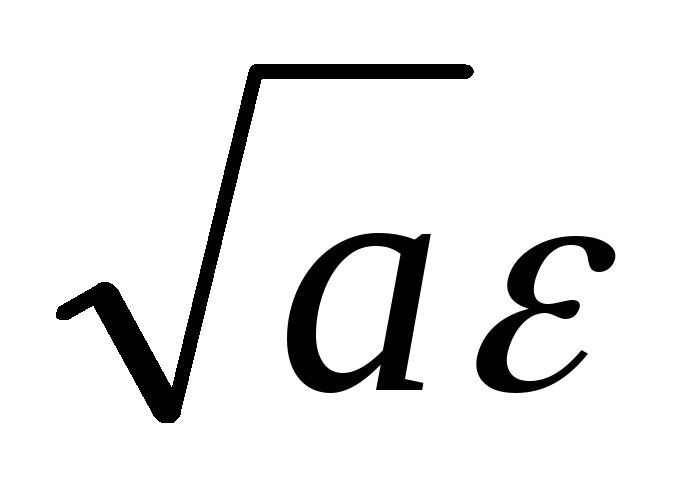 таке, що із нерівності
таке, що із нерівності 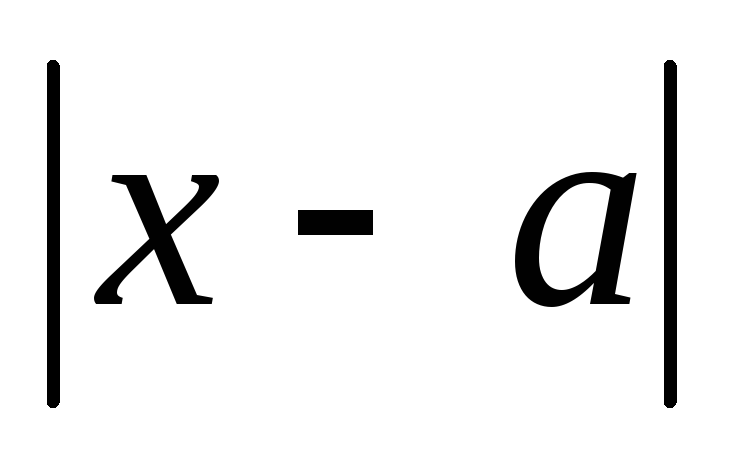 <δ
випливає
<δ
випливає 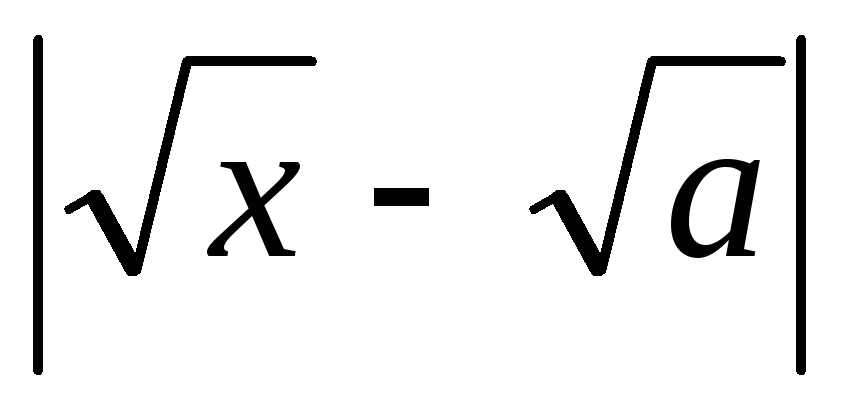 <
< 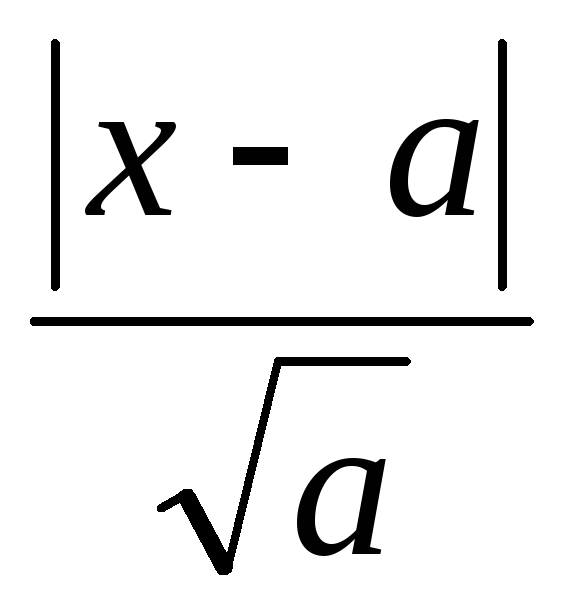 <
<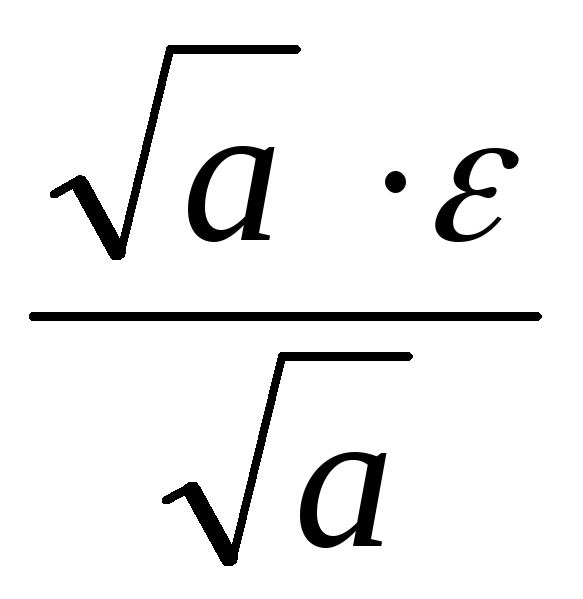 =
ε. Отже,
=
ε. Отже,
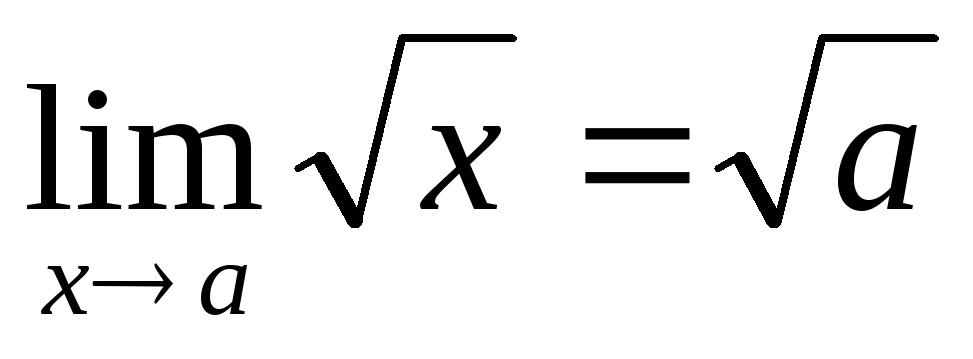 тобто
функція у =
тобто
функція у = 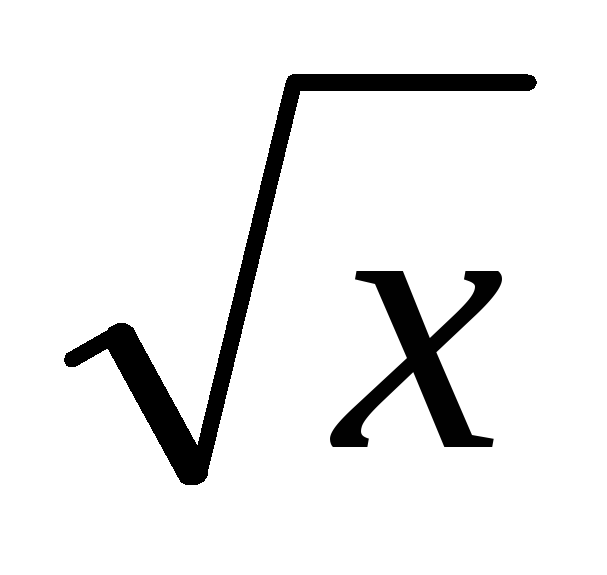 неперервна для всіх
χ
> 0.
неперервна для всіх
χ
> 0.
б) Доведемо, що 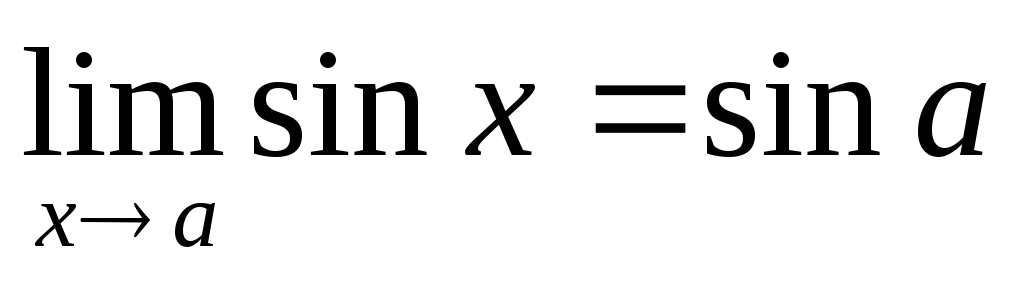 для
х
є
R.
для
х
є
R.
Оцінимо різницю
sin
х –
sin
а:
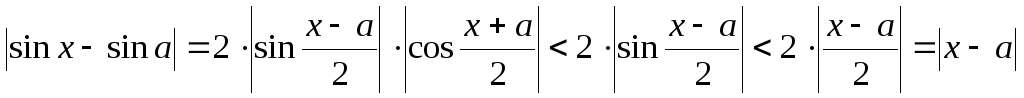
Легко бачити: |sin
х -
sin
α| <
ε, ε >
Ο, якщо
взяти |х
-
а|
менше
ε.
Таким чином, для
всякого
ε > 0 існує
δ = ε таке,
що із нерівності |х
— а|
<
δ випливає
|sin
х —
sin
а|
<
|х —
α|
<
δ =
ε.
Отже,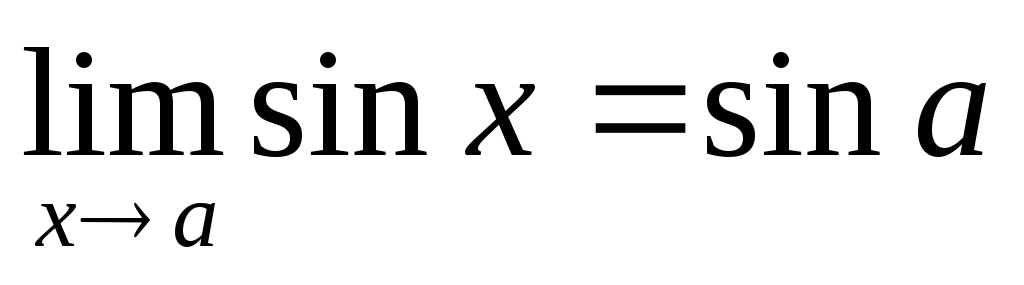 ,
тобто функція у
= sin
x
неперервна для всіх
х
є R.
,
тобто функція у
= sin
x
неперервна для всіх
х
є R.
5. Знайдіть границі,
користуючись неперервністю функції в
точці:
а) 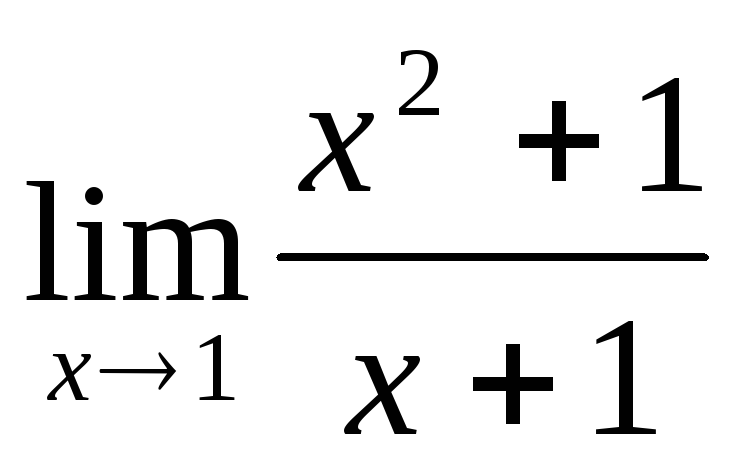 ;
б)
;
б) 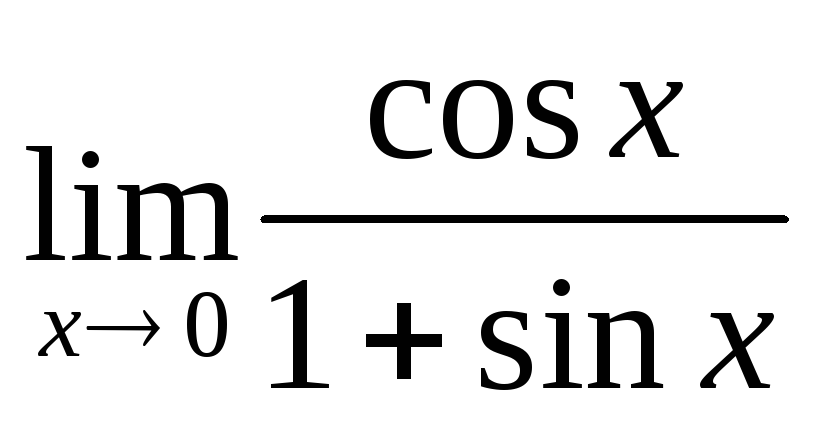 ;
в)
;
в)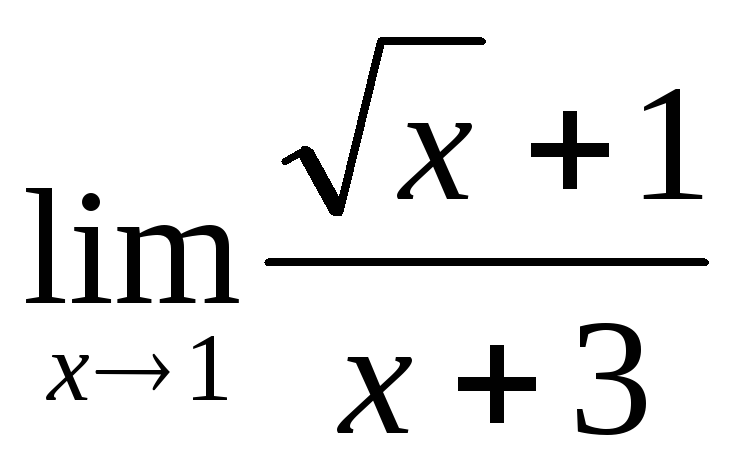 ;
г)
;
г) 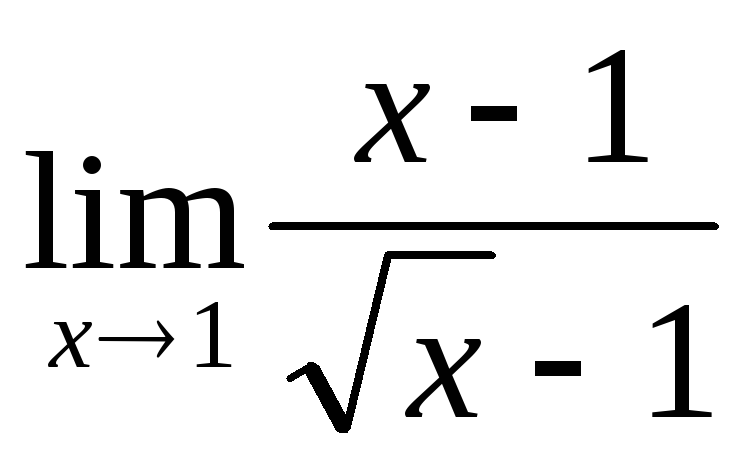 .
.
Відповідь:
а) 1; б) 1; в) 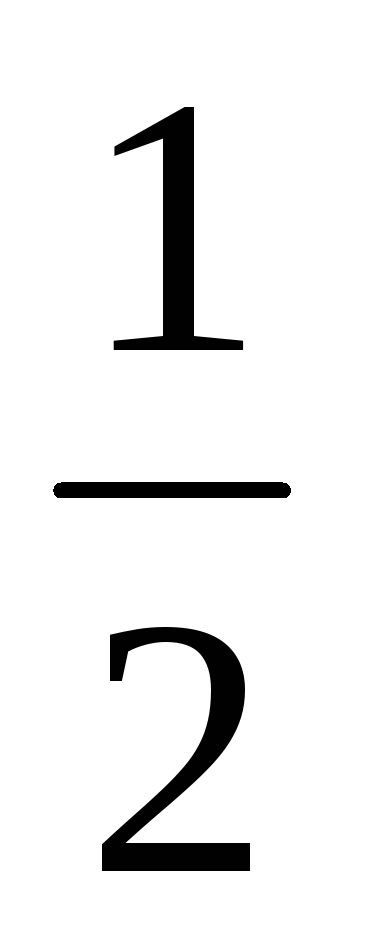 ;
г) 2.
;
г) 2.
IV. Домашнє завдання.
Розділ VI, § 6.
Запитання і завдання для повторення №
6. Вправи № 2 (6), 12 (1).
3
Роганін Алгебра 11 клас, урок 2