65. Теорема Пифагора. Квадрат гипотенузы прямоугольного тре­угольника равен сумме квадратов катетов.

66. Теорема, обратная теореме Пифагора. Если квадрат стороны тре­угольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный.

67. Средние пропорциональные в прямоугольном треугольнике. Вы­сота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотену­зу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу.

68. Если в трапецию можно вписать окружность, то радиус окруж­ности есть среднее пропорциональное отрезков, на которые точка каса­ния делит боковую сторону.

69. Отрезок общей внешней касательной к двум касающимся окруж­ностям радиусов r и R равен отрезку общей внутренней касательной, заключенному между общими внешними. Оба эти отрезка равны .

70. Метрические соотношения в треугольнике.

1. Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

2. Следствие из теоремы косинусов. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

3. Формула для медианы треугольника. Если т — медиана треуголь­ника, проведенная к стороне с, то , где а и b — остальные стороны треугольника.

4. Теорема синусов. Стороны треугольника пропорциональны сину­сам противолежащих углов.

5. Обобщенная теорема синусов. Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описан­ной около треугольника.

71. Формулы площади треугольника.

1. Площадь треугольника равна половине произведения основания на высоту.

2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

3. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.

4. Площадь треугольника равна произведению трех его сторон, де­ленному на учетверенный радиус описанной окружности.

5. Формула Герона.

72. Элементы равностороннего треугольника со стороной а. Пусть h, S, R, r— высота, площадь, радиусы описанной и вписанной окружности равностороннего треугольника со стороной а. Тогда , , , .

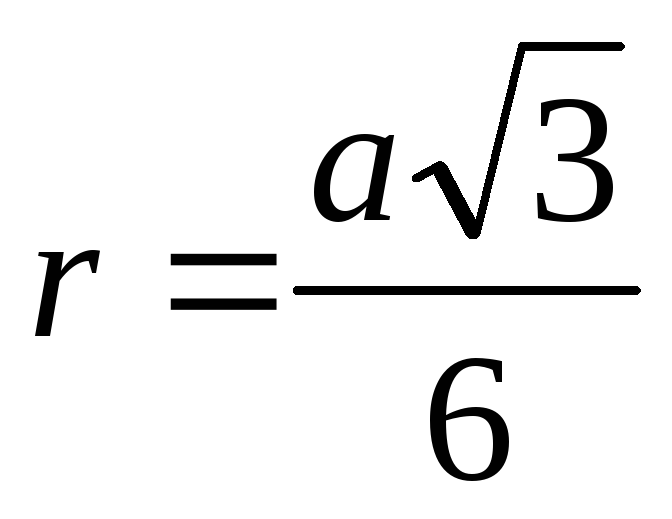73. Формулы площади параллелограмма.

1. Площадь параллелограмма равна произведению основания на вы­соту.

2. Площадь параллелограмма равна произведению его соседних сто­рон на синус угла между ними.

3. Площадь прямоугольника равна произведению двух его соседних сторон.

4. Площадь ромба равна половине произведения его диагоналей.

74. Площадь трапеции равна произведению полусуммы оснований на высоту.

75. Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.

76. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

77. Если в многоугольник можно вписать окружность, то его пло­щадь равна произведению полупериметра многоугольника на радиус этой окружности.

78. Если М — точка на стороне ВС треугольника ABC, то .

79. Если Р и Q — точки на сторонах АВ и АС (или на их продол­жениях) треугольника ABC, то

80. Длина окружности радиуса R равна 2R.

81. Площадь круга радиуса R равна .

Стереометрия

1. Аксиомы стереометрии.

Факты, непосредственно связанные с аксиомами

2. Через прямую и точку, не лежащую на этой прямой, проходит единственная плоскость.

3. Через две параллельные прямые проходит единственная плос­кость.

4. Через точку, не лежащую на данной прямой, проходит единствен­ная прямая, параллельная данной.

Параллельность в пространстве

2. Признак параллельности прямой и плоскости. Если прямая а па­раллельна некоторой прямой плоскости а, то прямая а параллельна плоскости а.

3. Если через прямую а, параллельную плоскости , провести плос­кость, пересекающую плоскость  по прямой b, то прямые а и b парал­лельны.

4. Если прямые а и b параллельны, а плоскость, проходящая че­рез прямую а, пересекается с плоскостью, проходящей через прямую b, то прямая пересечения плоскостей параллельна прямым а и b.

5. Транзитивность параллельности прямых в пространстве. Если прямая а параллельна прямой b, а прямая b параллельна прямой с, то прямая а параллельна прямой с.

6. Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересека­ющимся прямым другой плоскости, то плоскости параллельны.

7. Если две параллельные плоскости пересечены третьей, то пря­мые пересечения параллельны.

8. Транзитивность параллельности плоскостей. Если плоскость  параллельна плоскости , а плоскость  параллельна плоскости , то плоскость  параллельна плоскости .

9. Отрезки параллельных прямых, заключенные между параллель­ными плоскостями, равны.

10. Через точку, не лежащую в плоскости, проходит единственная плоскость, параллельная данной.