II Основные законы идеального газа.

Состояние данной массы газа характеризуют его параметры: объем V, давление р и температура Т. Законы, которые устанавливают взаимосвязь этих параметров при разных состояниях газа, называют газовыми законами. Процессы, протекающие при постоянстве одного из параметров, называют изопроцессами.

1). Закон Бойля - Мариотта: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная: рV=const при Т=const, m=const (8). Процесс, протекающий при постоянной температуре, называется изотермическим. Кривая, изображающая зависимость между величинами p и V, характеризующими свойства вещества при постоянной температуре, называется изотермой. Изотерма, соответствующая меньшей температуре, находится ближе к осям координат. Графики изотермического процесса в различных координатах:

2). Закон Гей-Люссака: при постоянном давлении объем данной массы идеального газа прямо пропорционален его абсолютной температуре: V/T=const при p=const и m=const (9). Процесс, протекающий при постоянном давлении, называется изобарным. Изобара, соответствующая более высокому давлению, лежит ниже изобары, соответствующей меньшему давлению. Графики изобарного процесса в различных координатах:

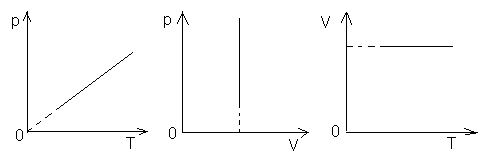
3). Закон Шарля: при постоянном объеме давление данной массы идеального газа прямо пропорционально его абсолютной температуре: р/Т=const при V=const и m=const (10). Процесс, протекающий при постоянном объеме, называется изохорным. Графики изохорного процесса в различных координатах:

4). Закон Авагадро: при одинаковых давлениях и температурах в равных объемах газа содержится одинаковое количество молекул.

Следствие: при нормальных условиях один моль любого газа занимает объем V=22,41 л (11).

Число молекул в 1 м³ при н.у. 2,7·10²⁵ (12) – число Лошмидта

5). Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов, т.е. р=р₁+р₂+…+р_n (13), где р₁, р₂,…р_n – парциальные давления – давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.

6). Объединенный газовый закон (уравнение Клапейрона): произведение давления данной массы идеального газа на его объем, деленное на абсолютную температуру, есть величина постоянная: 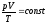, приm=const (14).

III Уравнение состояния идеального газа.

Возьмем 1 моль идеального газа при н.у. (р=1,013·10⁵ Па и Т=273 К). Согласно закону Авагадро V=22,4 л=22,4·10^-3 м³. Подставим эти данные в (14). Тогда : ,R=8,31 Дж/(моль·К) (15) – универсальная газовая постоянная. Если имеется не один, а ν молей, то объем газа будет в ν раз больше, т.е для какого-то произвольного объема V универсальная газовая постоянная R увеличится в ν раз, т.е. . Учитывая, чтоможно записать:(16) –уравнение состояния идеального газа (уравнение Менделеева - Клапейрона).

IV Температура, как мера средней кинетической энергии.

Определим соотношение между средней кинетической энергией теплового движения молекул <E> идеального газа и его абсолютной температурой Т. Согласно основному уравнению МКТ идеального газа . Из (16) выразим р, получим. Решив совместно систему из этих двух уравнений, получим:. Т.к.R и N_A - постоянные, то можно найти их отношение . Введем обозначение:k=1,38·10^-23 Дж/К (17) – постоянная Больцмана. Подставив ее в уравнение для энергии имеем: (18) –уравнение Больцмана.

Физ.смысл абсолютной температуры: абсолютная температура есть количественная мера средней кинетической энергии теплового (поступательного) движения молекул.

Установим связь между р, n и Т, для этого подставим (18) в основное уравнение МКТ. р=nkT (19).