II. Условия равновесия твёрдого тела. Виды равновесия

Статика изучает равновесие материальных точек или систем тел.

Система сил называется уравновешенной, если равнодействующая этой системы равна нулю. Точка приложения силы к абсолютно твёрдому телу может быть перенесена вдоль линии действия этой силы.

Тела, ограничивающие движение данного рассматриваемого тела, называются связями, а силы, действующие со стороны связей на данное тело, - силами реакции связей (опоры, подвесы).

Абсолютно твёрдое тело с закреплённой (неподвижной) осью вращения находится в равновесии при условии равенства нулю суммы всех n множеств М_i внешних сил относительно этой оси (правило моментов).

Если твёрдое тело может перемещаться поступательно, а также совершать вращательное движение вокруг некоторой оси, равновесие тела достигается при одновременном соблюдении двух условий:

где 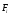- внешняя сила, действующая на тело,- момент этой силы, аn – число внешних сил.

Виды равновесия:

1. Равновесие тела в некотором положении называется устойчивым, если при любых малых отклонениях тела от этого положения, допускаемых связями, возникают силы или моменты сил, стремящиеся возвратить тело в исходное состояние (математический маятник, шарик внутри сферической поверхности).

2. Равновесие тела в некотором положении называется неустойчивым, если хотя бы при некоторых малых отклонениях тела от этого положения, допускаемых связями, возникают силы или моменты сил, стремящиеся ещё больше отклонить тело от начального положения (шарик на вершине сферической поверхности).

3. Равновесие тела в некотором положении называется безразличным, если при любых малых отклонениях тела от этого положения, допускаемых связями, не возникает сил или моментов сил, стремящихся возвратить тело в начальное положение или ещё более удалить тело от начального положения (шарик на гладкой горизонтальной поверхности).

III. Теорема Гюйгенса-Штейнера

Момент инерции тела относительно оси не проходящей через центр масс, равен сумме момента инерции относительно оси параллельной данной и проходящей через центр масс и произведение массы тела на квадрат расстояния между осями.

Лекция 8 Кинетическая энергия вращения твердого тела. Расчёт моментов инерции различных тел

План лекции

1. Работа и кинетическая энергия при вращательном движении

2. Расчёт моментов инерции различных тел

I. Работа и кинетическая энергия при вращательном движении.

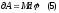- элементарная работа.

- полная работа.

- второй Закон Ньютона.

Подставим (*) в 5.

- теорема об изменении кинетической энергии.

II. Расчет моментов инерции различных тел

Для вычисления момента инерции твердого тела надо мысленно разбить его на малые элементы, точки которых можно считать лежащими на одинаковом расстоянии от оси вращения, затем найти произведение массы каждого элемента на квадрат его расстояния от оси и просуммировать полученное произведение.

Для подсчёта моментов инерции тел правильной геометрической формы, можно воспользоваться в ряде случаев приемами интегрированного исчисления.

Нахождение конечной суммы моментов инерции элементов тела заменим суммирование бесконечно большого числа моментов инерции вычислим для бесконечно малых элементов.

h - высота цилиндра

R – радиус цилиндра

Разобьём цилиндр на тонкие концентрические слои толщиной dr, пусть радиус некоторого слоя r, найдем его объём.

Так как все частицы слоя находятся на расстоянии r от оси, то их моменты инерции окажутся одинаковы.

а) Однородный сплошной цилиндр.

Если масса цилиндра m, то найдём плотность цилиндра.

По этой же формуле можно определить момент инерции диска.

б) Полый цилиндр с внутренним радиусом R и наружным r.

2. Момент инерции произвольного тела вращения.

Рассмотрим тело, поверхность которого образована вращением вокруг оси вращения плоской кривой (образующей).

Пусть известно плотность вещества и зависимость F(h). Разобьём тело на тонкие диски высотой dh.

Тогда момент инерции такого диска.

Найдём массу dm.

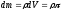
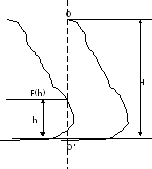
Момент инерции всего тела найдём интегрированием.

Литература

1. Стрелков С.П. Механика, Изд. 4-е, стер. СПб.: Лань, 2005 г.

2. Савельев И.В. Курс общей физики. Изд. 5-е, стер. СПб.: Лань, 2006 г.

3. Фриш С.Э., Тиморева А.В. Курс общей физики:-Т.1. Изд. 11-е, стер. СПб.: Лань, 2006 г.

4. Грабовский Р.И. Курс физики. Изд. 9-е, стер. СПб.: Лань, 2006 г.