Лекция 14 Реальный газ

План лекции

1. Межмолекулярное взаимодействие

2. Уравнение Ван-дер-Ваальса

3. Изотермы Ван-дер-Ваальса

I Межмолекулярное взаимодействие.

Разряженные реальные газы при не слишком низких температурах с достаточной степенью точности подчиняются законам идеальных газов. Повышение давления приводит к уменьшению среднего расстояния между молекулами, поэтому необходимо учитывать объем молекул и взаимодействие между ними.

Реальные газы – газы, свойства которых зависят от взаимодействия молекул. При их рассмотрении необходимо учитывать силы межмолекулярного взаимодействия.

Атомы и молекулы вещества – сложные системы движущихся заряженных частиц, между которыми действуют силы притяжения и отталкивания электрического происхождения. Эти силы короткодействующие. Они становятся пренебрежимо малыми уже на расстояниях порядка трех – четырех диаметров молекулы, причем силы отталкивания убывают с расстоянием быстрее, чем силы притяжения. Рассмотрим две молекулы 1 и 2. Проведем через центры молекул ось r в направлении от 1 молекулы ко 2 (рис.а). F_пр<0, F_от>0. График зависимости сил от расстояний между молекулами рас.б. График проекции на ось r результирующей силы Рис.а. Из графика видно: 1) если r<r_o – преобладают силы отталкивания, 2) если r>r_o – преобладают силы притяжения, 3) если r=r_o – равны.

II Уравнение Ван–дер-Ваальса.

Чтобы получить уравнение состояния реального газа, необходимо внести в уравнение состояния идеального газа поправки, учитывающие силы межмолекулярного взаимодействия.

1) Поправка на собственный объем молекул (учет сил отталкивания). Так как молекулы реальных газов нельзя считать материальными точками, они сами занимают некоторый объем и этот объем недоступен для их движения. Учтем этот недоступный объем в виде поправки b (b - объем, занимаемый самими молекулами), тогда уравнение состояния для 1 моля примет вид p(V_m -b)=RT. Для подсчета недоступного объема предположим, что имеют место только парные столкновения молекул. Сталкиваясь, две молекулы сближаются на расстояние d, равное эффективному диаметру. Для центров обеих молекул недоступным является объем сферы радиуса d. 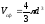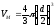, а объем молекулы, тогда, т.е. для двух молекул недоступным будет объем превышающий объем одной молекулы в 8 раз. В расчете на одну молекулу, недоступным оказывается объем, равный учетверенному объему одной молекулы.

2) Поправка на внутреннее давление (учет сил притяжения). Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема 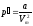(1), где а – постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения,V_m – молярный объем.

Вводя эти поправки, получим уравнение Ван-дер-Ваалься для моля газа – уравнение состояния реальных газов. (2), т.к.V=νV_m=>V_m=V/ν, тогда (3), где а иb – постоянные для каждого газа величины, определяемые опытным путем. Уравнение Ван-дер-Ваальса более точно, чем уравнение Менделеева – Клапейрона, но и оно приближенное.