VI Адиабатический процесс. Политропный процесс.

Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой. К адиабатическим процессам можно отнести быстропротекающие процессы. Из I начала термодинамики (δQ=dU+δA) для адиабатического процесса следует, что δА= - dU (14), т.е. внешняя работа совершается за счет изменения внутренней энергии системы. Перепишем (14) в виде (*) Продифференцируем уравнение состояния идеального газа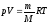, получим(**). Разделим (**) на (*). Разделив переменные и учитывая, что С_р/С_V=γ, найдем dp/p= - γdV/V. Интегрируя это уравнение в пределах от р₁ до р₂ и соответственно от V₁ до V₂, а затем потенцируя, получим илиp₁V₁^γ=p₂V₂^γ. Т.к. состояния 1 и 2 выбраны произвольно, то можно записать pV^γ=const (15). – уравнение адиабатического процесса (уравнение Пуассона). Используя уравнение Менделеева – Клапейрона можно получить TV^γ-1=const (16) и T^γp^1-γ=const (17). В этих уравнениях γ – называется показателем адиабаты (или коэффициентом Пуассона).

Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой, но адиабата более крута, чем изотерма. Это объясняется тем, что при адиабатном сжатии 1-3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.

Найдем работу если газ адиабатически расширяется от объемаV₁ до V₂, то его температура уменьшается от Т₁ до Т₂ и работа расширения идеального газа (18). Из уравнения (16). Заменим Т наV. (19). Работа, совершенная газом при адиабатическом расширении 1-2 , меньше, чем при изотермическом. При адиабатическом расширении происходит охлаждение газа, а при изотермическом температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Все рассмотренные процессы протекают при постоянной температуре. (При изотермическом с=, т.к. С=Q/mdT, а dT=0. При адиабатном Q=0 и с=0.). Процесс, в котором теплоемкость остается постоянной, называется политропным. Уравнение политропы pVⁿ=const где - показатель политропы. С=0,n=γ – уравнение адиабаты. С=,n=1 – уравнение изотермы. С=С_р, n=0 – уравнение изобары. С=С_V, n=- уравнение изобары.

Лекция 12 Второе начало термодинамики

План лекции

1. Круговой процесс

2. Энтропия

3. Различные формулировки второго начала термодинамики

4. Цикл Карно

1. Круговой процесс.

Круговым процессом называется процесс при котором система пройдя через ряд состояний возвращается в исходное.

Графически, цикл, совершаемый идеальным газом можно разбить на процессы: 1-2 расширение, 2-1 сжатие.

Работа, совершаемая газом за цикл, определяется площадью охватываемой замкнутой кривой. Если за цикл совершается работа А=∫pdv>0 то он называется прямым. Если А “-” то обратным.

Прямой цикл используется в тепловых двигателях – периодически действующих двигателях совершающих работу за счет полученной извне теплоты. Обратный цикл используется в холодильных машинах – периодически действующих установках в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой.

В результате кругового процесса система возвращается в исходное состояние тогда первое началоQ=A т.е. работа совершаемая за циклом равна количеству полученной из вне теплоты. В результате кругового процесса система может теплоту получать и отдавать. .

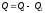Термический КПД для кругового процесса равен отношению полезной работы А совершаемой за цикл к количеству теплоты от нагревателя Q.

₁=(Q₁-Q₂)/Q=1-Q₂/Q₁

Термодинамический процесс называется обратимым если он может происходить как в прямом так ив обратном направлении. А если нет то необратимый.

Любой равновесный процесс является обратимым. Обратимые процессы – это идеализация реальных процессов. Они необходимы

1. Т.к. многие процессы близки к обратимым.

2. Обратимые процессы являются наиболее экономичными: имеют 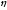_max, что позволяет указать пути повышения КПД реальных тепловых двигателей.