III Первое начало термодинамики.

Закон сохранения энергии применительно к термодинамическим процессам называется первым началом термодинамики.

Все количество теплоты, переданное системе, идет на изменение внутренней энергии системы и совершаемую системой работу – первое начало термодинамики. Q=ΔU+A (10).

Если система периодически возвращается в исходное состояние, то изменение ее внутренней энергии ΔU=0. Тогда, согласно I началу термодинамики А=Q. Это значит, что невозможно создать периодически действующий механизм, который совершал бы работу, превышающую получаемую им энергию.

Воображаемый механизм, совершающий работу, большую получаемой энергии, называется вечным двигателем первого рода.

Другая формулировка I начала термодинамики: вечный двигатель первого рода невозможен.

Выражение (10) в дифференциальной форме будет иметь вид: δQ=dU+δA (11). Где dU – бесконечно малое изменение внутренней энергии системы, δA – элементарная работа, δQ – бесконечно малое количество теплоты.

IV Теплоемкость.

Теплоемкость – скалярная физическая величина, характеризующая связь между количеством сообщенного системе тепла и изменением температуры этой системы.

Различают полную, молярную и удельную теплоемкости.

1. Полная теплоемкость численно равна количеству тепла, которое необходимо сообщить системе, чтобы повысить ее температуру на единицу. С_п=δQ/dT (1).

2. Молярная теплоемкость численно равна количеству тепла, которое необходимо сообщить одному молю вещества, чтобы повысить его температуру на единицу. С=δQ/(νdT) (2).

3. Удельная теплоемкость численно равна количеству тепла, которое необходимо сообщить единице массы вещества, чтобы повысить его температуру на единицу. с=δQ/(mdT) (3).

Из (2) и (3) найдем связь между молярной и удельной теплоемкостями. Учитывая, что ν=m/M, получим С=Мс (4). Теплоемкость зависит от свойств вещества, от температуры, а для газов от характера процесса, при котором система получает тепло. Рассмотрим теплоемкость газов.

1. V=const. I начало термодинамики: δQ=dU+δA, т.к.δА=рdV, а при V=const, dV=0=> δQ=dU. Подставим в (2), получим С_V =dU/(νdT). Для идеального газа , тогда(5). Для одноатомного газаi=3 и , для двухатомного – i=5 и , для многоатомного –i=6 и .

2. р=const. Продифференцируем уравнение Менделеева – Клапейрона по Т: pdV=νRdT. Из (2) ,(6). Из (5) и (6)C_p=C_V+R (7) – уравнение Майера. Разделим (6) на (5) (8).

V Применение первого начала термодинамики к изопроцессам.

1 Изохорный процесс (V=cobst). δА=рdV=0 и I начало термодинамики (9).

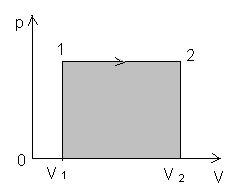
2 Изобарный процесс (p=const). Начертим график в координатах рV. При изобарном процессе работа газа при расширении объема от V₁до V₂ равна и определяется площадью прямоугольника. Воспользуемся уравнением Менделеева – Клапейрона(10) и выразим.Физический смысл R: R численно равно работе изобарного расширения 1 моля идеального газа при нагревании его на 1 К.

I начало термодинамики для изобарного процесса: δQ=dU+δA (11).

3 Изотермический процесс (Т=const). Найдем работу изотермического расширения газа: 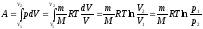(12), т.кp₁V₁=p₂V₂. Т.к. T=const, то dU=0 и из I начала термодинамики δQ=δA (13).