Вопросы к допуску

1. Дайте определение величины углового ускорения.

2. Что называют моментом силы?

3. Что такое момент импульса тела?

4. Какая величина является моментом инерции материальной точки?

5. Чему равен момент инерции тела?

6. В каких единицах измеряют угловое ускорение, момент силы, момент инерции, момент импульса?

7. Сформулируйте закон динамики вращательного движения

8. Запишите закон динамики вращательного движения.

9. Какое вращение тела называют равноускоренным, каковы его условия?

10. Как направлены векторы ε, М и момент импульса тела L?

11. От чего зависят: а) угловое ускорение маятника, б) момент инерции маят­ника, в) момент силы, действующий на маятник?

12. Какая зависимость лежит в основе динамического метода измерения мо­мента инерции ?

13. Какие величины определяют наклон прямой на графике ε= f(M)?

14. Как в работе изменяют момент силы?

15. Какие величины в работе измеряют для определения величин ε и М?

16. Как можно изменять момент инерции маятника в данной работе?

17. Запишите закон динамики вращательного движения для случая, когда момент инерции вращающегося тела не изменяется.

Контрольные вопросы

1. Опишите метод изучения закона динамики вращательного движения.

2. Чем обусловлена погрешность в этой работе?

3. Для каких целей используются графики?

4. Из каких соображений выбирают для графика размер осей?

5. Что указывают на осях графика?

6. Как выбирают границы интервалов на графиках?

7. Как выбирают масштаб числовых осей графика? Как его указывают?

8. Как проводят экспериментальную кривую на графике?

9. Через какую точку необходимо провести прямую на графике, если зави­симость линейная?

10. Как определяют угловой коэффициент линейной зависимости?

11. Как находят случайную погрешность углового коэффициента?

12. Какие источники случайной погрешности приводят к "разбросу" точек на графиках при изучении движения?

13. Прямой круглый однородный конус имеет массу m и радиус основания R. Найти момент инерции конуса относительно его оси.

14. Найти момент инерции однородного куба относительно оси, проходящей через центры противолежащих граней. Масса куба m, длина ребра a.

Лабораторная работа № 3 определение момента инерции металлических колец

ЦЕЛЬ: Определение момента инерции кольца с помощью маятника Максвелла.

ОБОРУДОВАНИЕ: Маятник Максвелла, штангенциркуль.

Теоретиченская часть

Подтвердым понимается в механике такое тело, взаимное расположение частей которого остается неизменным во время движения. Такое тело выступает при движении как единое целое.

Простейшим движением твердого тела является движение, при котором тело перемещается параллельно самому себе. Такое движение называют поступательным. При поступательном движении твердого тела все его точки имеют одинаковую скорость и описывают траектории одинаковой формы, только смещенные по отношению друг к другу.

Другим простейшим видом движения твердого тела является вращение тела вокруг оси. При вращении различные точки тела описывают окружности, лежащие в плоскостях, перпендикулярных оси вращения.

Если за время dt тело поворачивается на угол dφ, то путь ds, проходимый за это время какой-либо точкой P тела, будет равен ds = rdφ, где r – расстояние от точки P до оси вращения. Разделив ds на dt, найдем скорость точки P:

.

Величина одинакова для всех точек тела и представляет собой угловое перемещение тела за единицу времени. Эта величина называется угловой скоростью тела ω.

Скорости различных точек вращающегося вокруг некоторой оси твердого тела определяются формулой

,

где r – расстояние точки до оси вращения; скорость пропорциональна этому расстоянию.

Величина ω, вообще говоря, меняется с течением времени. Если вращение происходит равномерно, т.е. с постоянной угловой скоростью, то ω можно определить, зная период вращения Т:

.

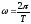Вращение характеризуется направлением оси вращения и величиной угловой скорости. Их можно объединить вместе, введя вектор угловой скорости , имеющий направление оси вращения и равный по величине угловой скорости. Из двух направлений оси вращения вектору угловой скорости принято приписывать то, которое связано с направлением вращения так называемым правилом винта, т.е. то направление, в котором ввинчивается винт (с правой резьбой), вращающийся одинаково с твердым телом.

Любое движение твердого тела сводится к этим простейшим видам: произвольное движение твердого тела можно представить в виде совокупности поступательного движения всего тела со скоростью какой-либо его точки О и вращения вокруг оси, проходящей через эту точку. При этом поступательная скорость зависит от того, какая именно точка тела выбрана в качестве основной. Угловая же скорость от этого выбора не зависит: при любом выборе точки О проходящая через нее ось вращения будет иметь одинаковое направление и будет одинаковой величина угловой скорости. В этом смысле можно сказать, что угловая скорость имеет «абсолютный» характер, - можно говорить об угловой скорости вращения твердого тела, не указывая при этом, через какую именно его точку проходит ось вращения. Поступательная же скорость такого «абсолютного» характера не имеет.

Обычно в качестве «основной» точки О выбирают центр инерции тела. Поступательная скорость есть при этом скорость перемещения центра инерции.

Так как при поступательном движении все точки тела имеют одинаковую скорость, то кинетическая энергия равна

,

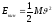где 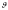- скорость тела, а М – его полная масса. Это выражение - такое же как если бы со скоростью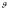двигалась одна материальная точка массы М. Ясно, что поступатель6ное движение твердого тела вообще ничем существенным не отличается от движения материальной точки.

Определим теперь кинетическую энергию вращающегося тела. Для этого разделим его мысленно на отдельные элементарные части, настолько малые, чтобы их можно было считать движущимися как материальные точки. Если m_i – масса i-го элемента, а r_i– его расстояние до оси вращения, то его скорость равна υ_i= r_iω, где ω – угловая скорость вращения тела. Кинетическая энергия этого элемента равна и, просуммировав эти энергии, получим полную кинетическую энергию тела

Стоящая здесь в скобках сумма зависит от того, с каким именно твердым телом мы имеем дело (от его формы, размеров и распределения масс в нем), а также от того, как расположена в нем ось вращения. Эта величина, характеризующая твердое тело и выбранную ось вращения, называется моментом инерции тела относительно данной оси.

Обозначим его буквой J:

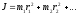
Если твердое тело – сплошное, то его нужно разделить на бесконечно большое количество бесконечно малых частей; суммирование в написанной формуле заменяется тогда интегрированием.

Тогда кинетическая энергия вращающегося тела может быть написана в виде

.

Кинетическую энергию произвольно движущегося твердого тела можно представить в виде суммы поступательной и вращательной энергий:

.

Индекс «0» у момента инерции означает, что он берется относительно оси, проходящей через центр инерции.

В таком виде эта формула имеет реальный практический смысл лишь, если в процессе движения ось вращения сохраняет постоянное направление в теле. В противном случае момент инерции должен браться в разные моменты времени относительно различных осей, т.е. перестает быть постоянной величиной.

Рассмотрим твердое тело, вращающееся вокруг некоторой оси Z, не проходящей через центр инерции. Кинетическая энергия этого движения есть 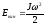, гдеJ – момент инерции относительно оси Z. С другой стороны, можно рассматривать это же движение как совокупность поступательного движения со скоростью υ центра инерции и вращения (с той же угловой скоростью ω) вокруг оси, проходящей через центр инерции параллельно оси Z. Если а есть расстояние центра инерции от оси Z, то его скорость υ = а·ω. Поэтому кинетическую энергию тела можно представить в также и в виде

.

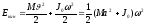Сравнив оба выражения, найдем

.

Эта формула связывает момент инерции тела относительно какой-либо оси с моментом инерции относительно другой оси, параллельной первой и проходящей через центр инерции. Очевидно, что J всегда больше, чем J_0. Другими словами, при заданном направлении оси минимальное значение момента инерции достигается для оси, проходящей через центр инерции.

ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ

Маятник Максвелла представляет собой небольшой диск (маховик), насажанный туго на ось, который опускается под действием силы тяжести на двух нитях, предварительно намотанных на ось маховичка (см. Рис.1).

Рис.1

Нити во время движения вниз разматываются до полной длины, раскрутившийся маховичок продолжает вращательное движение в том же направлении и наматывает нити на ось, вслед­ствие чего он поднимается вверх, замедляя при этом свое вращение. Дойдя до верхней точки, диск опять будет опускаться вниз и т. д.. Махо­вичок будет совершать колебания вверх и вниз, поэтому такое устройство и называют маятни­ком.

Составим уравнение движения маховичка. Пусть Р – сила тяжести, F - сила натяжения

одной нити, R - радиус валика, J - момент инерции маховичка, тогда урав­нение поступательного движения маховичка имеет вид: Р - 2F = ma (1) где а - ускорение центра масс.

Уравнение для вращательного движения маховичка:

(2)

где 2FR - момент сил натяжения нитей; 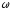- угловая скорость вращения дис­ка. Скорость поступательного движения маховичка связана с его угловой скоростью следующим соотношением:V = R, а их ускорения связаны так:

a = R(3) (Так как ускорение - производная скорости по времени). Решая уравнения (1), (2), (3), относительно трех неизвестных, находим ускорение центра масс:

(4)

и момент инерции: (5)

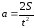Ускорение и сила натяжения нитей не зависят от того, куда движется махо­вичок - вверх или вниз. При колебаниях маятника меняет знак скорость, а ускорение и силы сохраняют направление. Ускорение а может быть вычис­лено по известному времени движения и проходимому маятником расстоянию из уравнения: , отсюда :(6)

Из уравнения (1), учитывая, что Р = mg, имеем:

(7)

Из формул (5)-(7) имеем: 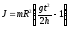Учитывая, что проще измерить, диаметр осиd = 2R, получим:

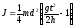(8)

где J - момент инерции маятника в кг·м², d - внешний диаметр оси маятника, вместе с намотанной на нее нитью подвески в м; t- время падения маятника в с ;g - ускорение силы тяжести в м/с²; h- длина маятника, равная максимальной высоте его подъема в м ; m- масса маятника вместе с кольцом в кг, определяемая по формуле: m = m₀ + m_p + m_k,

где m₀ - масса оси маятника в кг; m_p - масса ролика в кг ;m_k - масса наложенного на ролик кольца в кг.

Таким образом, формула (8) позволяет определить момент инерции маят­ника, причём все величины, входящие в формулу, легко измеримы.

Общий вид маятника Максвелла показан на рис. 2. Основание 1 оснащено регулируемыми ножками 2, которые позволяют произвести выравнивание прибора. В основании закреплена колонка 3, к которой прикреплен неподвижно верхний кронштейн 4 и нижний крон­штейн 5. На верхнем кронштейне находится электромагнит 6, фотоэлек­трический датчик 7 и вороток 8 для закрепления и регулирования длины бифилярной подвески маятника. Нижний кронштейн вместе с прикреплен­ным к нему фотоэлектрическим датчиком 9 можно перемещать вдоль колонки и фиксировать в произвольно выбранном положении. Маятник 10 установки - это ролик, закрепленный на оси, на который накладываются заменные кольца 11, изменяя таким образом момент инерции системы.

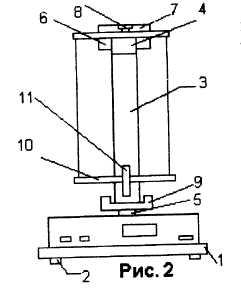
Маятник с наложенным кольцом удер­живается в верхнем положении электромагни­том. Длина маятника определяется по шкале на колонке прибора. С целью облегчения этого измерения нижний кронштейн был оснащен красным указателем, помещенным на высоте оптической оси нижнего фотоэлектрического датчика.