
matan_obschee
.docx|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1,2,3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для
того чтобы функция
|
|
2.
если функция
|
|
3.
если функция
|
|
4.
если функция
|
|
В
область определения функции
|
|
В
область определения функции
|
|
В
число первых трех членов разложения
функции
|
|
Геометрический
смысл производной есть ( |
|
Дифференциал
функции
|
|
Дифференциальный
бином
|
|
Для
множества натуральных (N),
рациональных (Q),
целых (Z),
действительных (R)
из приведенных включений верными
являются: ( |
|
Для
множества
|
|
Для
функции
|
|
Для
функции
|
|
Для
функции
|
|
Для
функции
|
|
Для
функции
|
|
Для
функции
|
|
Если
|
|
Если
|
|
Если
|
|
Если
|
|
Если
|
|
Если
|
|
Если
|
|
Если
|
|
Значение
предела
|
|
Значение
предела
|
|
Значение
предела
|
|
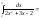
Интеграл
|
|
Интеграл
|
|
Интеграл
|
|
Исследовать
на непрерывность функцию
|
|
Исследовать
на непрерывность функцию
|
|
Исследовать
на непрерывность функцию
|
|
Исследовать
на непрерывность функцию
|
|
Какие из следующих утверждений верны? |
|
Множество действительных чисел А называется ограниченным сверху, если существует такое действительное число М, что: (любой элемент множества А не больше указанного числа М) |
|
На
всей числовой прямой непрерывна
фунция: ( |
|
Наименьшая
из всех верхних граней ограниченного
сверху множества |
|
Найти
асимптому кривой |
|
Найти
производную функции
|
|
Неопределенный
интеграл
|
|
Неопределенный
интеграл
|
|
Область
определения функции
|
|
Область
определения функции
|
|
Первообразной
для функции
|
|
Первообразной
для функции ( |
|
Первообразной
для функции
|
|
Переменная
|
|
Пересечение
множеств
|
|
Пересечением
двух множеств А и В (обозначается
|
|
Последовательность
|
|
Последовательность
|
|
Последовательность
|
|
Предел
отношения приращения функции
|
|
Предел
функции
|
|
|
|
Производная
второго порядка функции
|
|
Производная
второго порядка функции
|
|
Производная
второго порядка функции
|
|
Производная
пятого порядка функции
|
|
Производная
функции
|
|
Производная
функции
|
|
Производная
функции
|
|
Производная
функции в точке
|
|
Производная
функции
|
|
Производная
функции
|
|
Производная
функции, заданной параметрически
|
|
Производная
функция
|
|
Производной
n-ного
порядка функции y=cosx
является ( |
|
Промежутки
монотонности функции
|
|
Промежутки
монотонности функции
|
|
Рациональную
дробь
|
|
Рациональную
дробь
|
|
Рациональную
дробь
|
|
Рациональную
дробь можно представить в виде суммы
следующих простых дробей: ( |
|
Следующие
равенства верны (
|
|
Следующие
равенства верны ( |
|
Следующие
равенства верны ( |
|
Следующие
равенства верны ( |
|
Следующие
равенства верны ( |
|
Следующие
равенства верны ( |
|
Следующие
равенства верны( |
|
Следующие
равенства верны( |
|
Теорема
Коши. Пусть функции |
|
Теорема
Лагранжа. Пусть на отрезке
|
|
Точка
x=0
не входит в область определения
функции: ( |
|
Точки
разрыва функции
|
|
Точки
разрыва функции
|
|
Уравнение
касательной к кривой y=f(x)
в точке
|
|
Учитывая
|
|
Физический смысл первой производной функции есть (скорость изменения функции). |
|
Функции
1)
|
|
Функции,
определенные на всей числовой прямой:
( |
|
Функция
|
|
Функция
|
|
Число
а называется пределом последовательности
|
|
Число А называется пределом функции f(x) при x→+∞, если для любого числа ε>0 существует число σ=σ(ε)>0, что для всех x, удовлетворяющих неравенству x>σ выполняется неравенство: (-ε<f(x)-A<ε ; |f(x)-A|<ε ; A-ε<f(x)<A+ε) |
|
Число А называется пределом функции f(x) при x→a, если для любого числа ε>0 существует число σ=σ(ε)>0, что для всех x, удовлетворяющих неравенству |x-a|<σ выполняется неравенство: (|f(x)-A|<ε ; -ε<f(x)-A<ε ; A-ε<f(x)<A+ε) |
|
Члены
в разложении функции
|

 (
(

 (
(

 (
(


 (
(
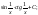
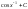
 (
(
 )
) (
(
 )
) (0,25;
(0,25;
 )
) (-0,6;
(-0,6;
 )
) (3lne;
3; 4/2)
(3lne;
3; 4/2) (
(


 (
( )
) (0;
ln1)
(0;
ln1) (1/2;
0,5)
(1/2;
0,5) (
( )
) (
( )
) (
( ).
). (
( ).
). (
( ).
). (
( ).
). (
( ).
). (
( ).
). (
( ).
). (
( ,
, ).
). (
( ,
, ).
). (
( ,
, ).
). (
( ,
, ).
). (
( ,
, ).
). (
( ,
, ).
). (
( ,
, ).
).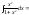 (
( ,
, ).
). принадлежит
промежутку: (
принадлежит
промежутку: ( )
) равен:
(ln1)
равен:
(ln1) (
(
 (
(
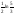 ).
). (
(
 ,
,
 ,
,
 ).
). (
(
 ;
;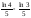 )
) (
3ln5-3ln3, 3(ln5-ln3), 3ln5/3)/
(
3ln5-3ln3, 3(ln5-ln3), 3ln5/3)/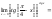 (
( )
) (
( )
) (
( )
) (
( )
) (
(
 )
) (
(
 )
) (
( ,
,
 ).
). (
(
 ;
; )
) (
(
 ;
; )
) (12)
(12) (2/7)
(2/7) (7/72)
(7/72) ,
,
 : (
: ( ,
, /
/
 ,
,
 )
) ,
,
 :
(
:
( ,
,
 /
/
 ,
,
 )
) =
(
=
( ).
). =(
=( ).
). была
дифференцируема в точке
была
дифференцируема в точке
 ,
необходимо и достаточно, чтобы в точке
,
необходимо и достаточно, чтобы в точке
 существовала конечная производная
существовала конечная производная

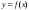 дифференцируема
внекоторой точке, то она и непрерывна
в этой точке
дифференцируема
внекоторой точке, то она и непрерывна
в этой точке в некоторой точке имеет производную,
то она непрерывна в этой точке
в некоторой точке имеет производную,
то она непрерывна в этой точке непрерывна в некоторой точке, то она
и дифференцируема в этой точке
непрерывна в некоторой точке, то она
и дифференцируема в этой точке входит промежуток:
входит промежуток:

 входит промежуток: (
входит промежуток: ( /
/ /
/
 )
) по формуле Маклорена входит функция:
(
по формуле Маклорена входит функция:
(
 /
/
 /
/ )
) ,
где
,
где
 -угол
между касательной и осью Ох).
-угол
между касательной и осью Ох). равен (
равен ( ,
, ,
,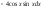 ).
). ,
где m,n,p
- рациональные числа, интегрируется
в следующих случаях: (
,
где m,n,p
- рациональные числа, интегрируется
в следующих случаях: ( /
/
 /
/
 )
) /
/
 )
)

 но
соотношение: (
но
соотношение: ( /
/
 /
/
 )
) значение
значение
 принадлежит промежутку:(
принадлежит промежутку:(
 /
/
 )
)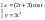 производная
производная
 равна (
равна ( ,
, ).
). :
(
:
(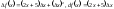 /
/
 /
/
 )
) верно
равенство: (
верно
равенство: ( /
/
 )
) верно
следующее утверждение: (
верно
следующее утверждение: (
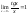 /
/ /
/
 )
) следующее
утверждение верно: (
следующее
утверждение верно: ( /
/
 является
точкой разрыва первого рода, скачок
/ разрывная функция )
является
точкой разрыва первого рода, скачок
/ разрывная функция ) ,
то
,
то
 (
( ,
, ).
). ,
то значение производной
,
то значение производной
 находится в промежутке (
находится в промежутке ( ,
, ,
, ).
). ,
то значение производной
,
то значение производной
 находится в промежутке (
находится в промежутке ( ,
, ,
,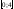 ).
). ,
то производная функции в точке
,
то производная функции в точке
 (2,
(2,
 ,
,
 ).
). ,
то: (
,
то: ( /
/
 /
/
 )
) ,
то: (
,
то: ( /
/ )
) и
и
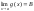 ,
где A,
B
< ∞, то: (
,
где A,
B
< ∞, то: ( ;
; ;
; )
) и
и
 то:
(
то:
( /
/
 )
) находится в промежутке промежутку
([0;5] ; [-1,6];
находится в промежутке промежутку
([0;5] ; [-1,6];
 )
) находится
в промежутке ([0;5] [-1:6] [0;4])
находится
в промежутке ([0;5] [-1:6] [0;4]) принадлежит
промежутку ([-1;6]; [0,4];
принадлежит
промежутку ([-1;6]; [0,4];
 )
) равен: (
равен: (
 )
) равен: (
равен: ( /
/
 )
) равен: (
равен: ( /
/
 )
) : (
: (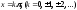 точки-бесконечного
разрыва /
точки-бесконечного
разрыва /
 -устранимая
точка разрыва,
-устранимая
точка разрыва,
 -точки-бесконечного
разрыва )
-точки-бесконечного
разрыва ) в точке
в точке
 :
(
:
( не существует / Функция имеет разрыв
2-го рода в точке
не существует / Функция имеет разрыв
2-го рода в точке
 )
) в точке x=0
: (f(+0)=1)
в точке x=0
: (f(+0)=1) ;
(
;
( - не устранимая точка разрыва)
- не устранимая точка разрыва) /
/
 /
/
 )
) называется:
(точной верхней гранью и обозначается
sup
A
)
называется:
(точной верхней гранью и обозначается
sup
A
) : (
: ( /
/
 /
/
 )
)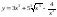 (
( ,
, ,
,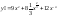 ).
). равен: (
равен: ( /
/
 )
)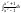 равен: (
равен: ( /
/
 )
) является
(-∞<x≤-
является
(-∞<x≤- или
или
 ≤ x<+∞)
≤ x<+∞) является
(-∞<x≤2
или 6 ≤ x<+∞)
является
(-∞<x≤2
или 6 ≤ x<+∞) (
(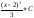 ,
,
 ).
). (
( ,
,
 ).
). является
функция ( arctgx+C,
-arcctgx+C).
является
функция ( arctgx+C,
-arcctgx+C).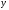 называется однозначной функцией
называется однозначной функцией
 от
переменной
от
переменной
 в
данной области измерения
в
данной области измерения
 ...
(каждому значению
...
(каждому значению
 ставится
в соответствие одно определенное
значение
ставится
в соответствие одно определенное
значение
 принадлежащее
некоторому множеству
принадлежащее
некоторому множеству
 )
) и
и
 называется
множество (
называется
множество ( состоящее
из всех тех и только тех элементов,
каждый из которых принадлежит обоим
множествам одновременно)
состоящее
из всех тех и только тех элементов,
каждый из которых принадлежит обоим
множествам одновременно) )
называется: (
)
называется: (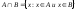 /множество, состоящее из элементов,
принадлежащих и множеству А, и множеству
В)
/множество, состоящее из элементов,
принадлежащих и множеству А, и множеству
В) называется бесконечно большой, если:
(для любого числа A>0
существует номер N
такой, что при n>N
выполняется неравенство
называется бесконечно большой, если:
(для любого числа A>0
существует номер N
такой, что при n>N
выполняется неравенство
 / для любого числа A>0
существует номер N
такой, что при n>N
выполняется неравенство
/ для любого числа A>0
существует номер N
такой, что при n>N
выполняется неравенство
 )
) называется сходящейся, если существует
такое вещественное число a,
что: (
называется сходящейся, если существует
такое вещественное число a,
что: ( найдется номер N
такой, что при всех
найдется номер N
такой, что при всех
 элементы
элементы
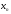 этой
последовательности удовлетворяют
неравенству
этой
последовательности удовлетворяют
неравенству
 / последовательность
/ последовательность
 является бесконечно малой / в любой
является бесконечно малой / в любой
 -
окрестности точки a,
находятся все элементы последовательности
-
окрестности точки a,
находятся все элементы последовательности
 ,
начиная с некоторого номера(зависящего
от
,
начиная с некоторого номера(зависящего
от )
)
)
) называется
неограниченной , если: (
называется
неограниченной , если: (

 /
/


 )
) к
приращению аргумента
к
приращению аргумента
 при стремлении
при стремлении
 к
нулю называется (производной функции
f(x)
)
к
нулю называется (производной функции
f(x)
) равен: (
равен: ( )
) принадлежит
промежутку: (
принадлежит
промежутку: (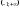 /
/
 )
) равна (
равна ( ,
, ).
). (
( ).
). (
( ,
,
 ,
,
 ).
). (5!,
(5!,
 ,
120).
,
120). равна (
равна ( ,
, ).
). равна (
равна ( ,
, ,
, ).
). является (
является ( ).
). ,
если
,
если
 (0,sin0).
(0,sin0). равна
(
равна
(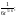
 ;
;
 равна
(
равна
(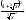
 ;
;

 где
где
 ,
, -дифференцируемые
функции, находится по формуле (
-дифференцируемые
функции, находится по формуле ( ).
). +
+ :
(
:
( /
/
 /
/
 )
) ).
). :
(
:
( монотонно возрастает /
монотонно возрастает /
 монотонно возрастает /
монотонно возрастает / монотонно убывает)
монотонно убывает) :
(
:
( монотонно
возрастает /
монотонно
возрастает /
 монотонно
убывает /
монотонно
убывает /
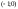 монотонно
возрастает)
монотонно
возрастает) можно
представить в виде суммы следующих
простых дробей (
можно
представить в виде суммы следующих
простых дробей (

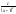 )
) можно
представить в виде суммы следующих
простых дробей (
можно
представить в виде суммы следующих
простых дробей (

 )
) можно
представить в виде суммы следующих
простых дробей (
можно
представить в виде суммы следующих
простых дробей (



 ;
; )
) ,
,
 ,
,
 ).
). ,
,
 ,
,
 ).
). ,
, ,
, ).
). ,
,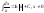 ,
, ).
). ;
; ;
;
 )
)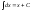 ;
; ;
;
 )
) ),
), ,
, ).
). ,
,
 ,
,
 ).
). и
и
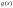 непрерывны
на отрезке
непрерывны
на отрезке
 и дифференцируемы на интервале
и дифференцируемы на интервале
 Тогда существует точка
Тогда существует точка
 ,
в которой справедлива формула: (
,
в которой справедлива формула: ( /
/
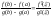 )
) определена функция
определена функция
 ,
которая непрерывна на отрезке
,
которая непрерывна на отрезке
 и дифференцируема на интервале
и дифференцируема на интервале
 .
Тогда существует точка
.
Тогда существует точка
 ,
в которой справедлива формула: (
,
в которой справедлива формула: ( /
/
 )
) /
/
 )
) (
функция непрерывна)
(
функция непрерывна) (х1=1,
х2=5)
(х1=1,
х2=5) имеет
вид (
имеет
вид ( ).
). ,
производная функции
,
производная функции
 равна (
равна ( ).
). ,
2)
,
2)
 ,
3)
,
3)
 имеющие
точки разрыва 2-го рода: (3), 2) / 3) / 2))
имеющие
точки разрыва 2-го рода: (3), 2) / 3) / 2)) /
/
 /
/
 )
) была первообразной
была первообразной
 на
на
 необходимы
чтобы: (F
непрерывна на
необходимы
чтобы: (F
непрерывна на
 /
/
 существует
существует
 /
/

 )
) на
на
 обладает следующими свойствами: (на
отрезке
обладает следующими свойствами: (на
отрезке
 функция возрастает / в точке
функция возрастает / в точке
 достигает максимума / На отрезке
достигает максимума / На отрезке
 функция убывает)
функция убывает) если
: (
если
: ( /
/


 :
: / для любого
/ для любого
 существует
номер N
такой, что при
существует
номер N
такой, что при
 выполняется
неравенство
выполняется
неравенство
 )
) по
формуле Маклорена: (
по
формуле Маклорена: ( /
/
 )
)