13. Классификация чмп

В [3] предложена классификация ЧМП, основанная на хар актере информации, получаемой от ЛПР на фазе анализа.

Первая группа ЧМП — прямые ЧМП, в которых ЛПР непос редственно назначает веса критериев и корректирует их на основе полученных решений.

Для второй группы ЧМП задача ЛПР состоит в сравнении многокритериальных решений. Эта группа называется ЧМП оценки векторов.

Третья группа требует от ЛПР наложения ограничений на значения критериев и, следовательно, на область достижимых значений. ЧМП этой группы называются ЧМП поиска удовлет ворительных решений.

Перед тем как перейти к рассмотрению ЧМП каждой групп ы, следует указать на общие предварительные этапы,встре чающиеся во многих ЧМП. Прежде всего рекомендуется произ­ вести нормирование критериев, определив диапазон их измене ния от 0 до 1:

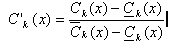
где — минимально и максимально возможные значения k -го критерия; Ck (х) — промежуточное значение.

Кроме того, как это было показано выше (табл. 3.1), для каждого из критериев вычисляется наилучшее значение при предположении, что он является единственным. Вектор таких (недостижимых одновременно) значений помогает ЛПР оценить пределы возможного.

14. Прямые человекомашинные процедуры

В основе прямых ЧМП лежит предположение, что человек может искать наилучшее решение путем непосредственного наз начения ряда параметров (например, весов критериев) и сравн ения получающихся решений.

В качестве примера прямых ЧМП рассмотрим процедуру SIGMOP (последовательный генератор информации для много- целевых задач [9]). В ней ЛПР пытается найти хорошее решен ие путем назначения весов критериев ( wi ) и уровней допустим ых значений по всем критериям одновременно ( Ci >= li )•

Лицо, принимающее решение, задает начальные значения wi и li ( i = 1, ..., N). Далее на фазе расчетов компьютер определяет новую область D достижимых значений переменных и на- ходит в ней значение глобального критерия (1), а также всех отдельных критериев. Значения всех критериев, не удовлетвор яющих начальным уровням, предъявляются ЛПР. После этого ЛПР меняет веса и ограничения в любой последовательности до тех пор, пока процедура не даст ему приемлемого решения.

Если критериев мало (два - три), то данная процедура мож ет быть достаточно удобной. Однако при возрастании числа критериев для ЛПР становится все сложнее оценить влияние , на получаемые решения каждого из весов и каждого из огран ичений. Поэтому, вероятно, количество прямых ЧМП сравнит ельно невелико [3].

15. Процедуры оценки векторов

В основе этих процедур лежит предположение, что ЛПР может непосредственно сравнивать решения, предъявляемые ему в виде векторов в критериальном пространстве, и системат ически искать в этом пространстве наилучший вектор.

Одной из наиболее известных ЧМП оценки векторов явля- ется процедура Дайера-Джиофриона (Д-Д) [10]. Она начинаетс я с выбора какой-либо точки в критериальном пространстве (рис. 3.6).

Рис. 3.6. Поиск решения в критериальном пространстве

В этой точке ЛПР определяет градиент глобальной целевой функции следующим образом. Один из критериев считается опорным. Берется небольшое изменение значения этого критер ия (в сторону улучшения) от начального. Перед ЛПР ставятся вопросы типа: какое изменение по иному критерию эквивал ентно заданному изменению опорного критерия? Ответы ЛПР определяют вектор (направление), вдоль, которого изменение глобального критерия будет наиболее эффективным. Вдоль это- го направления делается шаг определенной длины и получаются новые значения по всем критериям. Совокупность этих знач ений (вектор) предъявляется ЛПР вместе с первоначальным решением (соответствующим начальной точке). Далее перед ЛПР ставится вопрос: какое из решений лучше? Если лучше новое решение (назовем его Y 1 ), то делается еще шаг вдоль это-го же направления и вычисляется решение Y 2. Далее Y 1 и Y 2 предъявляются ЛПР. Если Y 2 лучше, то делается еще шаг в прежнем направлении, и т.д. Если Y 1 лучше, чем Y 2 , то в точк е Y 2 определяется новый градиент (направление) изменения

глобальной целевой функции (см. рис. 3.6), и т.д. Процедура заканчивается, если ЛПР признает очередное решение вполне для него удовлетворительным.

Другим наиболее известным методом, принадлежащим к данной группе, является метод Зайонца—Валлениуса [7]. Он представляет собой процедуру сужения множества значений весовых векторов wi . В начале задается вектор весов, имеющий равные компоненты. Далее выясняется значение глобального критерия. Обычно этому значению соответствует в области Доп устимых значений одна из вершин многоугольника. В смежных к ней вершинах подсчитываются значения весов критерие в, при которых данная вершина могла бы быть оптимальным решением однокритериальной задачи. Также в этих вершинах подсчитываются значения вектора оценок по критериям.

ЛПР попарно предъявляются векторы значений критериев в начальной точке и каждый из векторов значений критериев в смежных вершинах. При этом ЛПР ставит вопрос, какой кри териальный вектор предпочтительнее. Возможны три варианта ответа:

• предпочтительнее смежный критериальный вектор;

• предпочтительнее начальный критериальный вектор;

• нет четкого предпочтения.

На основе ответов ЛПР формируются ограничения на значения весовых коэффициентов критериев. Далее определяется центральная точка в допустимой области весовых коэффициент ов, опять вычисляется значение глобального критерия и т.д.

Доказано, что метод сходится к точке, соответствующей наибольшей полезности ЛПР, если априори неизвестная функц ия полезности ЛПР является вогнутой.

В отличие от прямых методов мы видим в ЧМП оценки векторов систематический поиск, помогающий ЛПР найти наилучшее решение.