
Задача 1.
Решение:
Мода – это наиболее часто встречающееся значение признака у единиц данной совокупности. В этом ряду распределения мода равна оценке 4 (хорошо) – это значение повторяется 24 раза, чаще, чем другие.
Медиана – значение признака, приходящееся на середину ранжированной совокупности. Для ее определения необходимо рассчитать сумму накопленных частот:
|
Балл оценки знаний студентов |
2 (неудовлетворительно) |
3 (удовлетворительно) |
4 (хорошо) |
5 (отлично) |
|
Число студентов |
9 |
12 |
24 |
15 |
|
Накопленные частоты |
9 |
9+12=21 |
21+24=45 |
45+15=60 |
Сумма частот равна 60, ее половина – 30. Накопленная сумма частот, впервые превышающая половину равна 45, ей соответствует значение признака, равное 4 (хорошо) - таким образом, 4 (хорошо) является медианой.
Квартиль - это значения признака, которые делят ранжированный ряд на четыре равные по численности части. Таких величин будет три: первая квартиль(Q1), вторая квартиль (Q2), третья квартиль (Q3). Вторая квартиль является медианой. В дискретном ряду численное значение квартили определяют по накопленным частотам. 60 / 4 = 15. Отсюда, первая квартиль Q1= 3 (удовлетворительно), третья квартиль Q3=4 (хорошо).
Дециль характеризует распределение величин совокупности, при котором девять значений дециля делят её на десять равных частей. Любая из этих десяти частей составляет 1/10 всей совокупности. 60 / 10 = 6. Так, первый дециль отделяет 10 % наименьших величин, лежащих ниже дециля от 90 % наибольших величин, лежащих выше дециля. D1 = 2 (неудовлетворительно), D9 = 5 (отлично) (сумма накопленных частот 9*6=54).
Задача 2.
Решение:
-
Определим индекс количества реализованной продукции - Iq:
100 + 20 = 120%, 120 / 100 = 1,2 – т.е. количество увеличилось в 1,2 раза;
-
Определим индекс цены - Ip:
-
+ 20 = 120%, 120 / 100 = 1,2 – т.е. цена возросла в 1,2 раза;
-
Определим индекс объема реализованной продукции, используя взаимосвязь индексов:
Ipq= Ip * Iq = 1,2 * 1,2 = 1,44 * 100% = 144%
Таким образом, стоимость реализованной продукции увеличилась на 44% .
Задача 3.
Решение:
-
О
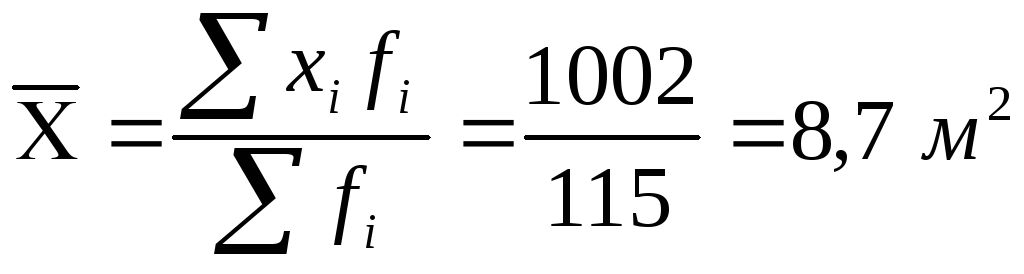 пределим
среднее значение жилой площади по
формуле средней арифметической
взвешенной:
пределим
среднее значение жилой площади по
формуле средней арифметической
взвешенной:
Для
расчетов построим таблицу, определив
середины интервалов:
![]() ;
;
![]() и т. д.
и т. д.
|
Группы семей xi |
Число семей fi |
Середина интервала xi′ |
xi fi |
Накопленные частоты |
Накопленные частоты, % к итогу |
|
3-5 |
10 |
4 |
40 |
10 |
8,7 |
|
5-7 |
21 |
6 |
126 |
31 |
27,0 |
|
7-9 |
28 |
8 |
224 |
59 |
51,3 |
|
9-11 |
30 |
10 |
300 |
89 |
77,4 |
|
11-13 |
26 |
12 |
312 |
115 |
100 |
|
Итого |
115 |
- |
1002 |
- |
- |
2) Определим моду по формуле
![]()
где хмо – нижняя граница значения интервала, содержащего моду;
iмо – величина модального интервала;
fмо – частота модального интервала;
fмо-1 – частота интервала, предшествующего модальному;
fмо+1 – частота интервала, следующего за модальным.
![]() =
9,7
м2
=
9,7
м2
3) Определим медиану по формуле
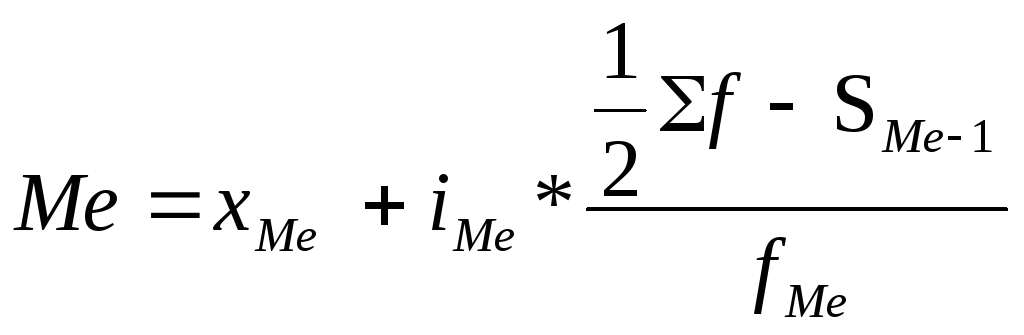
где хме – нижняя граница значения интервала, содержащего медиану;
iме – величина медианного интервала;
Σf – сумма частот;
Sме-1 – сумма накопленных частот, предшествующих медианному интервалу;
fме – частота медианного интервала.
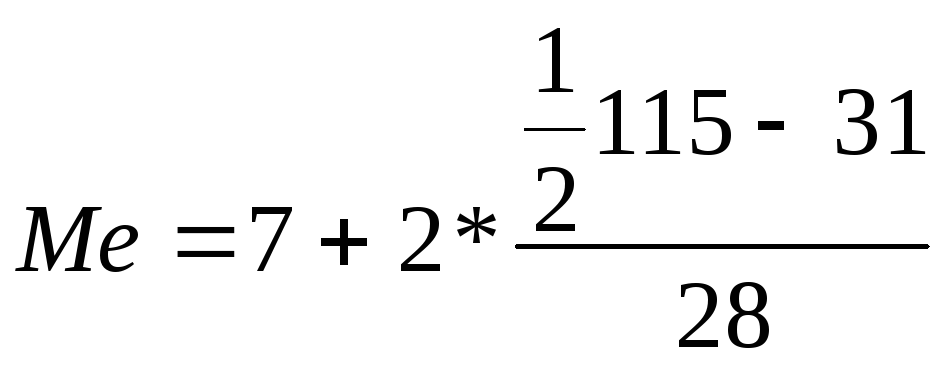 =
8,9
м2
=
8,9
м2
4) Определим квартильные значения
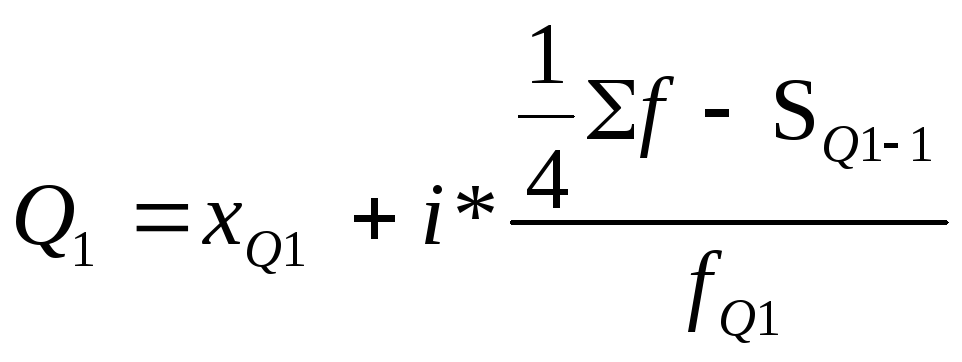 ;
;
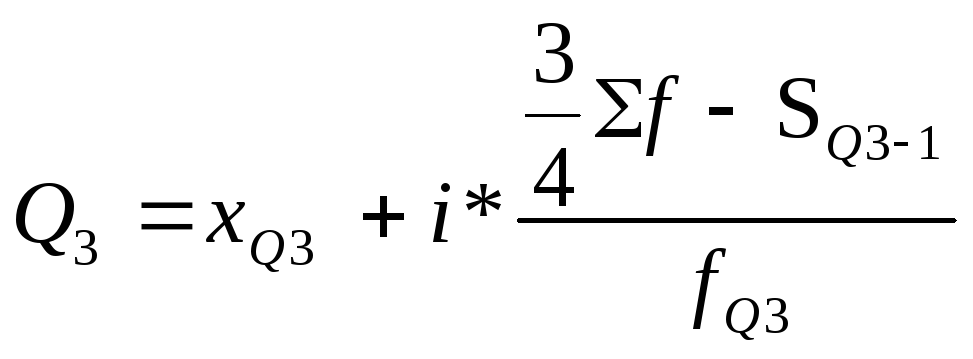
где хQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%;
хQ3 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%;
SQ1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
SQ3-1 – то же для верхнего квартиля;
fQ1 – частота интервала, содержащего нижний квартиль.
fQ3 – то же для верхнего квартиля.
Нижний квартиль находится в интервале 5-7, накопленная частота которого равна 31%. Верхний квартиль лежит в интервале 9-11 с накопленной частотой 89%. Отсюда получим:
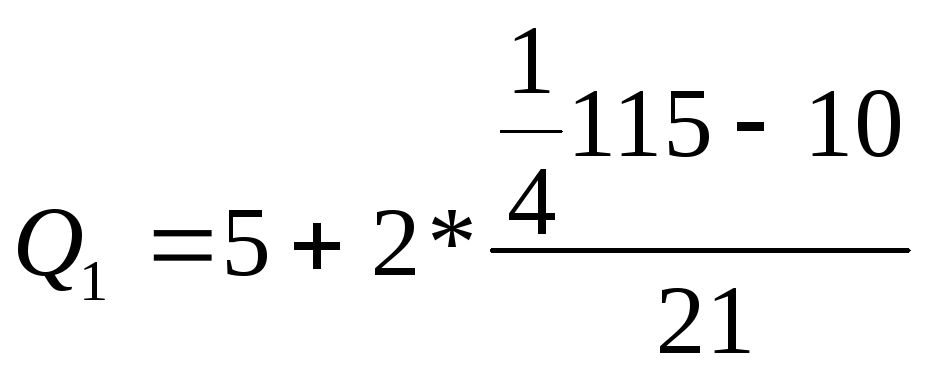 =
6,8
м2
=
6,8
м2
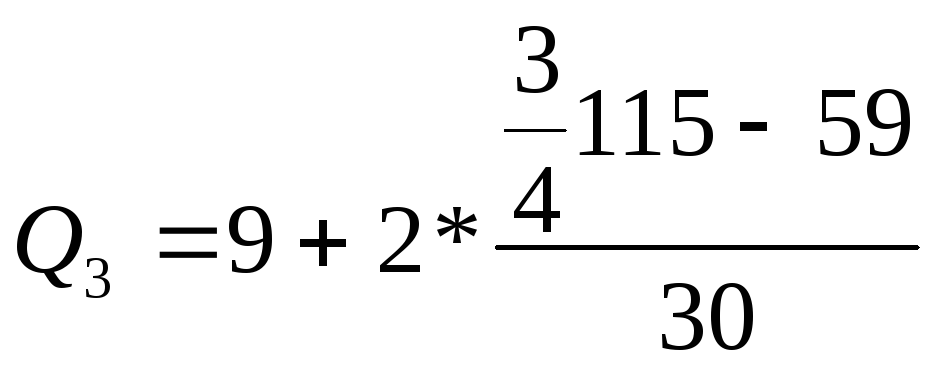 =
10,8
м2
=
10,8
м2
