Закон Ма;´люса

Пусть на поляризатор попадает плоскополяризованная волна (рис. 7), световой вектор Е₀ которой составляет  угол с плоскостью пропускания поляризатора.

Разложим вектор Е₀ на составляющие Е_┴ – перпендикулярно и Е_║ – параллельно плоскости поляризации падающей волны. В результате через поляризатор пройдет только составляющая исходного светового вектора Е_║, амплитуда которой равна

Е_║= E₀∙cos. (2)

Поляризо­ванный свет

Рис. 7. К формулировке закона Ма;´люса

Так как интенсивность I волны пропорциональна квадрату амплитуды E (то есть I ~ E²), то, возведя (2) в квадрат, получим

E_║² = E₀²∙cos²

или

I = I₀∙cos² (3)

где I₀ – интенсивность падающей на поляризатор поляризованной волны, I – интенсивность прошедшей волны,  – угол между плоскостью поляризации падающей волны и плоскостью пропускания поляризатора.

Формула (3) выражает закон Ма;´люса, который можно сформулировать так:

Закон Ма;´люса Интенсивность света, прошедшего через поляризатор, равна произведению интенсивности падающего на поляризатор поляризованного света и квадрата косинуса угла между плоскостью поляризации падающей световой волны и плоскостью пропускания поляризатора.

Следует отметить, что

при прохождении поляризованного света через поляризатор (поляроид) изменяется только интенсивность света, а ориентация плоскости поляризации остается неизменной.

Анализ поляризованного света

Человеческий глаз не отличает поляризованный свет от естественного. Поэтому для анализа света используют тоже поляризатор, который в этом случае называется анализатором. При этом возможны три случая.

1. Если на анализатор падает плоскополяризованный свет, то при вращении этого поляризатора (анализатора) вокруг луча будет изменяться угол , а следовательно, и интенсивность прошедшего света (см. закон Ма;´люса). При этом можно найти такое положение поляризатора, при котором свет через него не пройдет ( = 90^о). Это надежный способ убедиться в том, что падающий свет полностью поляризован.

2. Если при вращении поляризатора интенсивность прошедшего света изменяется, но полного гашения не происходит, то свет частично поляризован.

3. Если при вращении поляризатора вокруг светового луча интенсивности прошедшего света не изменяется, то падающий на поляризатор свет естественный

При падении на поляризатор естественного света интенсивность прошедшего поляризованного света не зависит от положения поляризатора и равна (без учета поглощения в поляризаторе) половине интенсивности падающего света.

Порядок выполнения

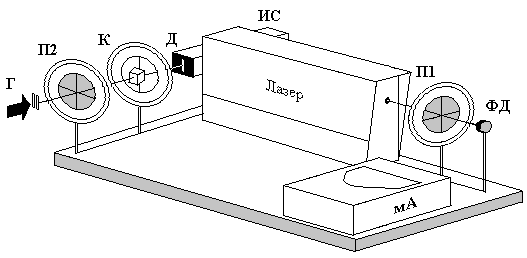
Рис. 8. Общий вид экспериментальной установки

Упражнение 1. Исследование света некогерентного источника

Рис. 9

Включите источник некогерентного света (ИС) и снимите с него или раскройте пошире щелевую диафрагму Д (рис.8). Установите на оптическую скамью перед источником держатель с поляроидом П2 и экран (рис. 9). Вместо экрана можно поместить лист бумаги. Вращая поляроид наблюдайте изменение интенсивности света на экране. Какой можно сделать вывод?

Упражнение 2. Проверка закона Ма;´люса

Рис. 10

На оптическую скамью установите держатель с поляроидом П1 и фотодиод ФД (рис.10). Включите лазер и, регулируя положение фотодиода ФД, добейтесь максимального отклонения стрелки прибора (миллиамперметра), который подключен к ФД. Вращением поляризатора П1 снова добейтесь максимального отклонения стрелки прибора (этот максимум может быть больше первого).

Заметьте это положение поляроида по шкале на его держателе. Считая теперь это значение за начало отсчета (0) поворачивайте поляризатор в любую сторону с шагом в 10, замеряя показания прибора и занося их в Таблице 1. Измерения проводятся до тех пор, пока поляроид П1 не совершит полный оборот. По данным из Таблицы 1 постройте график и проанализируйте его (— ордината, cos² — абсцисса).

Таблица 1

	0	10	20	30	40	50	60	70	80	90
I, мА
	180	170	160	150	140	130	120	110	100	90
I, мА
	180	190	200	210	220	230	240	250	260	270
I, мА
	360	350	340	330	320	310	300	290	280	270
I, мА
, мА
cos2

Упражнение 3. Исследование двойного лучепреломления

Рис. 11	Уменьшите ширину щелевой диафрагмы Д источника ИС или до 1 мм. На оптическую скамью перед источником установите держатель К с кристаллом исландского шпата. Вращая держатель с кристаллом, найдите положение, при котором глаз Г (рис. 11) видит два параллельных изображения щели. После появления двойного изображения щели дальнейшим вращением кристалла добейтесь максимального расстояния между ними.
Рис. 12	Поместите между кристаллом К и глазом Г держатель с поляроидом П2 (рис. 12). Вращением поляроида П2 добейтесь исчезновения одного изображения. Запишите в табл. 2 значение угла на шкале поляроида П2 — угол 1. Вращением поляроида по часовой стрелке добейтесь, чтобы вместо этого изображения щели появилось другое (ранее исчезнувшее), и занесите в табл. 2 угол2.
Это же значение угла занесите во вторую строку таблицы в графу для 1. Вращая поляроид дальше, снова поменяйте изображения местами, и снова запишите угол 2.

После поворота поляроида на 360 вычислите четыре значения угла , на который надо повернуть поляроид, чтобы попеременно можно было видеть только одно из двух изображений щели.

Вычислите доверительный интервал и проанализируйте полученные результаты.

Таблица 2

№	1	2	 = |1–2|		
1
2
3
4