2.2. Мультиплексор

Мультиплексор осуществляет подключение одного из входных каналов к выходному под управлением управляющего (адресующего) слова. Разрядности каналов могут быть различными, мультиплексоры для коммутации многоразрядных слов составляются из одноразрядных.

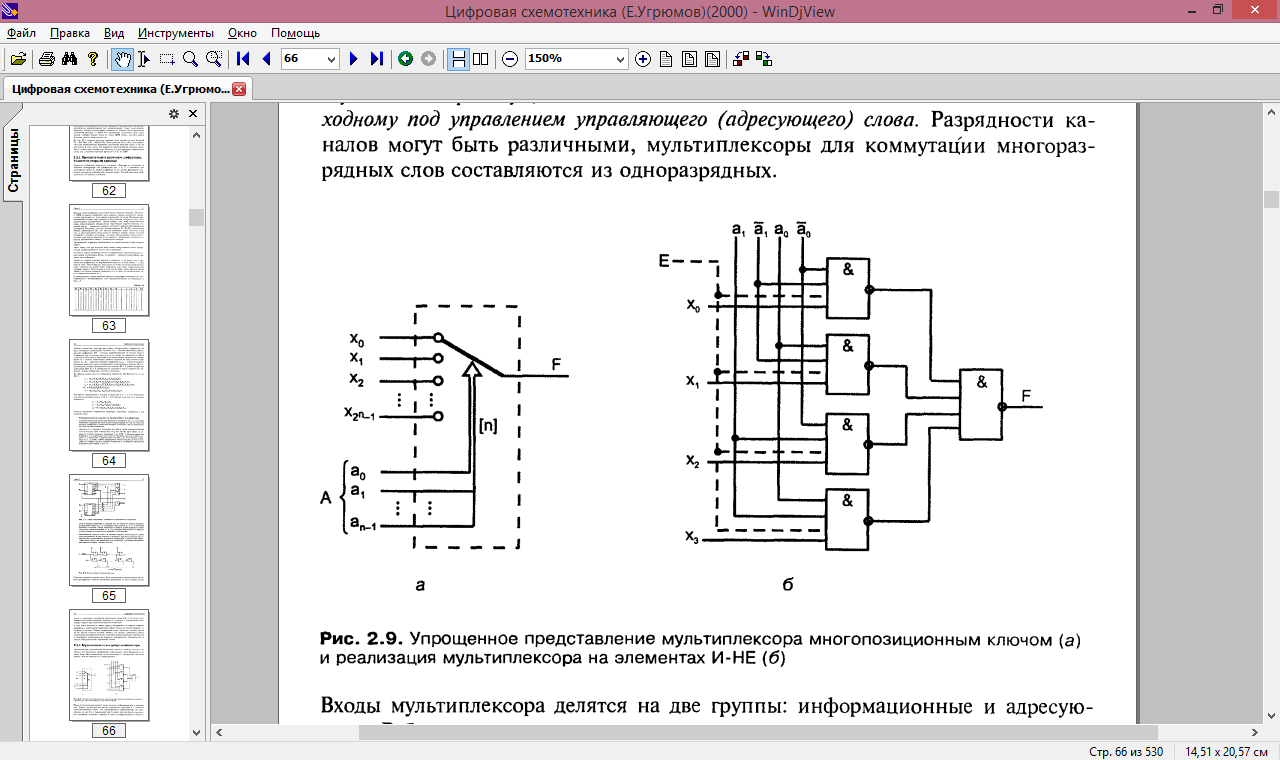
Рисунок 5. Упрощенное представление мультиплексора многопозиционным ключом (а) и реализация мультиплексора на элементах И-НЕ (б)

Входы мультиплексора делятся на две группы: информационные и адресующие. Работу мультиплексора можно упрощенно представить с помощью многопозиционного ключа. Для одноразрядного мультиплексора это представлено на рисунке 6, а. Адресующий код А задает переключателю определенное положение, соединяя с выходом F один из информационных входов x_i и т. д. Работа мультиплексора описывается соотношением

которое иногда называется мультиплексной формулой. При любом значении адресующего кода все слагаемые, кроме одного, равны нулю. Ненулевое слагаемое равно x_i, где i – значение текущего адресного кода.

Схемотехнически мультиплексор реализует электронную версию показанного переключателя, имея, в отличие от него, только одностороннюю передачу данных. На рисунке 6, б показан мультиплексор с четырьмя информационными входами, двумя адресными входами и входом разрешения работы. При отсутствии разрешения работы (Е=0) выход F становится нулевым независимо от информационных и адресных сигналов. В стандартных сериях размерность мультиплексоров не более 16х1.

2.3. Сумматор

Сумматоры выполняют арифметическое (в противоположность логическому) сло­жение и вычитание чисел. Имеют самостоятельное значение и являются также ядром схем арифметико-логических устройств (АЛУ), реализующих ряд разно­образных операций и являющихся непременной частью всех процессоров. Аппаратная сложность и быстродействие сумматора являются очень важны­ми параметрами и поэтому разработано множество вариантов сумматоров, которые имеют разветвленную классификацию. Выделяя главные варианты, остановимся на следующих типах сумматоров:

• одноразрядный сумматор;

• сумматор для последовательных операндов;

• сумматор для параллельных операндов с последовательным переносом;

• сумматор для параллельных операндов с параллельным переносом;

• сумматор групповой структуры с цепным переносом;

• сумматор групповой структуры с параллельным межгрупповым переносом;

• сумматор с условным переносом;

• накапливающий сумматор.

Наряду с сумматорами могут быть реализованы вычитатели, однако это поч­ти никогда не делается, поскольку вычитание выполняется через сложение с применением дополнительных либо обратных кодов.

2.3.1. Одноразрядный сумматор

Одноразрядный сумматор имеет три входа (два слагаемых и перенос из предыдущего разряда) и два выхода (суммы и переноса в следующий раз­ряд). Таблица истинности одноразрядного сумма­тора имеет следующий вид (таблица 5).

Таблица 5. Таблица истинности одноразрядного сумма­тора

ai	bi	ci–1	ci	si
0	0	0	0	0	1
0	0	1	0	1	1
0	1	0	0	1	1
0	1	1	1	0	0
1	0	0	0	1	1
1	0	1	1	0	0
1	1	0	1	0	0
1	1	1	1	1	0

Аналитические выражения функций суммы и пе­реноса (сигнал переноса обозначен через С от анг­лийского carry) имеют вид

В базисе Шеффера функции S_i и C_i выражаются следующим образом:

Непосредственное воспроизведение полученных формул на элементах двух­ступенчатой логики И-ИЛИ-НЕ приводит к применению элемента 2-2-2И- ИЛИ-НЕ для выработки сигнала переноса и элемента 3-3-3-3И-ИЛИ-НЕ. для сигнала суммы Такое решение используется в некоторых сериях микросхем, но более популярно решение, приводящее к некоторому сокращению аппаратной сложности схемы при сохранении минимальной задержки по цепи переноса. Идея этого решения состоит в использовании полученного уже значения в качестве вспомогательного аргумента при вычислении

2.3.1. Параллельный сумматор с последовательным переносом

Сумматор для параллельных операндов с последовательным переносом строится как цепочка одноразрядных, соединенных последовательно по це­пям переноса. Для схемы с одноразрядными сумматорами, вырабатываю­щими инверсии суммы и переноса, такая цепочка имеет вид, приведенный на рисунке 6, поскольку функции суммы и переноса самодвойственны. Там, где в разряд сумматора должны подаваться инверсные аргументы, в их ли­ниях имеются инверторы, а там, где вырабатывается инверсная сумма, ин­вертор включен в выходную цепь. Важно, что инверторы не входят в цепь передачи переноса — они при этом не замедляют работу сумматора в целом. Длительность суммирования для этой схемы в наихудшем случае распро­странения переноса по всей цепочке разрядов составит

где n — разрядность сумматора. Как и в других схемах с последовательным распространением сигналов от разряда к разряду, здесь время суммирования практически пропорциональ­но разрядности сумматора.

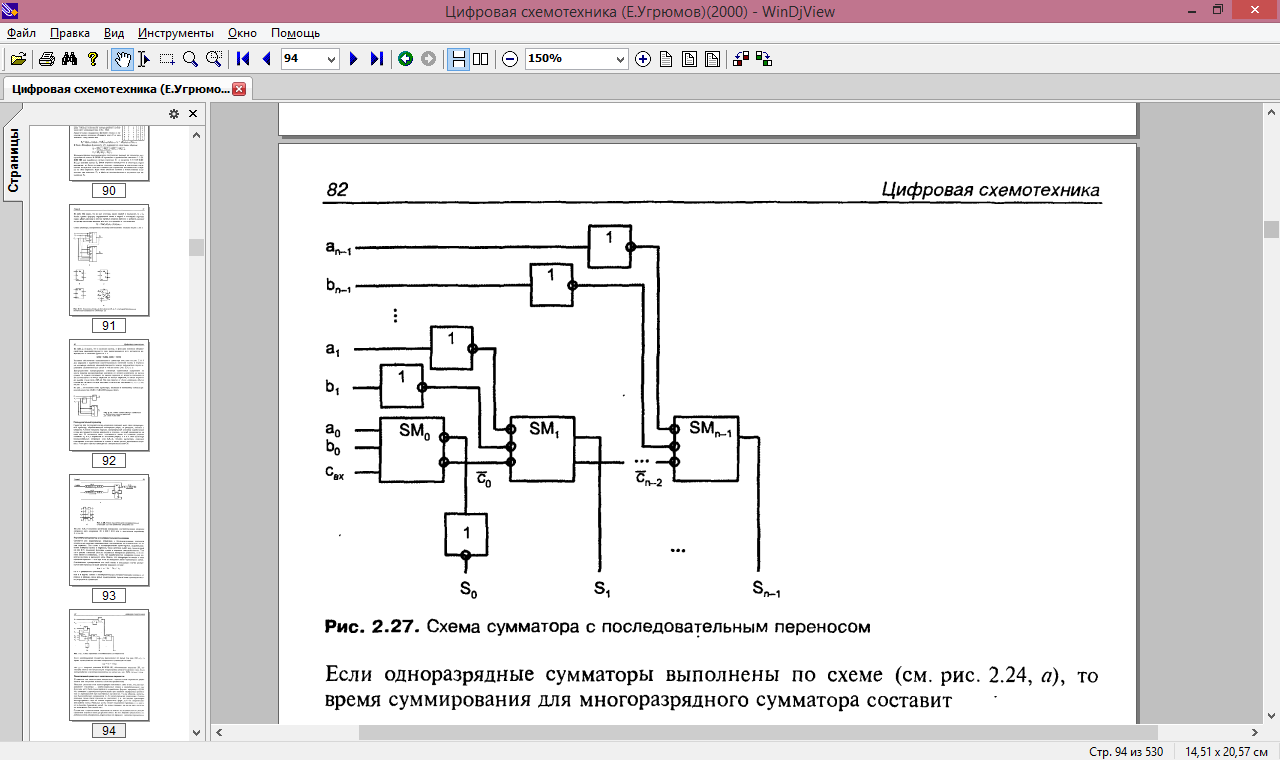
Рисунок 6. Схема сумматора с последовательным переносом

Если одноразрядные сумматоры выполнены по схеме, то время суммирования для многоразрядного сумматора составит

где t_ЛР— задержка элемента И-ИЛИ-НЕ, обозначенная индексом ЛР. по­скольку именно эти буквы входят в маркировку элементов данного типа. Если одноразрядные сумматоры выполнены по схеме (см. рисунок 6), то t_SM = nt_ЛР.

2.3.2. Параллельный сумматор с параллельным переносом

Сумматоры для параллельных операндов с параллельным переносом разра­ботаны для получения максимального быстродействия. Подход к решению этой задачи требует пояснений. Дело в том, что рассмат­риваемые сумматоры — комбинационные схемы и вырабатываемые ими функции могут быть представлены в нормальных формах, например в ДНФ. что приводит к двухъярусной реализации при наличии парафазных аргумен­тов и к трехъярусной при однофазных аргументах. Таким образом, предель­ное быстродействие оценивается (2...3) элементарными задержками. Однако реальные схемы таких пределов нс достигают, т. к. построение сумматоров многоразрядных слов на основе нормальных форм дало бы неприемлемо громоздкие схемы. Реальные схемы имеют модульную структуру, т. е. состо­ят из подсхем (разрядных схем), что резко упрощает их, но не дает предель­но возможного быстродействия. Сумматоры с параллельным переносом нс имеют последовательного распространения переноса вдоль разрядной сетки. Во всех разрядах результаты вырабатываются одновременно, параллельно во времени. Сигналы переноса для данного разряда формируются специальными схемами, на входы которых поступают все переменные, необходимые для выработки переноса, т. е. те, от которых зависит его наличие или отсутствие. Ясно, что это внешний входной перенос С_вх (если он есть) и значения всех разрядов слагаемых, младших относительно данного.

Рисунок 7. Структура сумматора с параллельным переносом