prak

Практические задания:

1. Записать со знаком факториала:1•2•3•4•4•5•6.

Это произведение чисел натурального ряда, но число 4 в нем встречается два раза, следовательно:

1·2·3·4·4·5·6 = 4·6!.

2. Записать с использованием знака факториала: 1•2•3•4•5•7•8•9•10.

В этом ряду отсутствует цифра 6. Умножим и разделим на 6 все выражение, тогда получим:

1•2•3•4•5•7•8•9•10=10! \ 6

3. Записать со знаком факториала: 1•3•5•6•7•8. Здесь пропущены два числа: 2 и 4.

Умножим и разделим на 2 и 4 все выражение, тогда получим:

1·3·5·6·7·8 = 7!

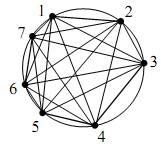
4. На окружности (рис. 3) расположены n точек. Каждая пара точек соединена прямой линией так, что в любой точке пересекаются не более двух прямых. Сколько точек пересечения имеется внутри круга? Точки пересечения линий с окружностью не учитывать.

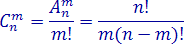
Одну точку пересечения можно получить, если взять четыре точки на окружности. Следовательно, каждой четверке точек окружности соответствует одна точка пересечения в круге. Число таких точек равно:

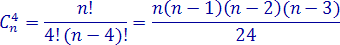
При n=5 имеется 5 точек, при  n=6 имеется 15 точек, при  n = 7 (как на рисунке 4.9.1) имеется 35 точек и т.д.

 

5. В урне пять шаров с номерами 1, 2, 3, 4, 5. Вынимают один шар и записывают его номер. Шар возвращают в урну и наугад снова выбирают один шар и номер его записывают справа от первой цифры. Получится двухразрядное число. Сколько возможно таких чисел?

На первом месте может стоять одна из пяти цифр, т. е. n = 5. На втором месте – также одна из пяти цифр. Следовательно, m = 5. Тогда искомое число nm = 5·5 = 25.

Среди всех этих 25 выборок существуют пары с одинаковыми цифрами.

6. Вернемся к примеру 2. Пусть шары извлекают три раза. Сколько получится трехзначных чисел?

На первом месте может стоять одна из пяти цифр, на втором – также одна из пяти, и на третьем – одна из пяти. Следовательно, число выборок равно 5·5·5 = 125.

7. Сколько существует трехразрядных шестеричных чисел?

В шестеричной системе счисления используются цифры 0,1,2,3,4,5. Первую цифру можно выбрать пятью способами, поскольку нуль не используем, так как число, начинающееся с нуля, не является трехразрядным. Вторая цифра может быть любой, в том числе и нулем, следовательно, ее можно выбрать шестью способами. То же самое относится и к цифре младшего разряда. Искомое число равно 5·6·6 = 180.

8. Сколько существует трехразрядных десятичных чисел, не содержащих повторяющихся цифр, если используются только цифры 3, 5, 9?

В данном случае n = 3, следовательно, искомое число равно 3! = 1·2·3 = 6. Все эти перестановки имеют вид: 359, 395, 539, 593, 953, 935.

9. Сколько различных слов можно составить из букв слова «километр», если под словом понимать всякую последовательность из восьми букв?

В заданном слове все буквы разные, следовательно, искомое число равно:

8! = 1·2·3·4·5·6·7·8 = 40320.

10. Сколько существует четырехбуквенных слов, в которых три буквы «а» и одна буква «в»?

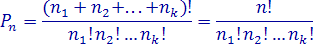
Здесь n₁ = 3, n₂ = 1, n = 4. Искомое число равно:

Это «слова» ааав, аава, аваа, вааа.

11. Сколько различных слов можно составить, переставляя буквы слова «ротор»? В слове «ротор» 5 букв. Из них две буквы «р», две буквы «о», одна буква «т».

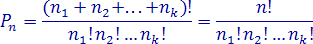
n = 5, n₁ = 2, n₂ = 2, n₃ = 1.

Искомое число различных слов равно:

среди которых такие «слова», как рроот, тоорр, ортро, оортр и т. д.

По формуле

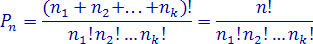
11. Сколько существует четырехзначных десятичных чисел, если в каждом из них все цифры разные?

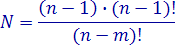
По условию примера имеем n = 10, m = 3, следовательно, искомое число согласно формуле равно:

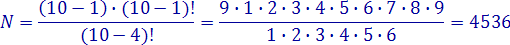
12. Сколько существует трехразрядных десятичных чисел, не содержащих четных цифр и не содержащих одинаковых цифр?

Нечетные цифры – это 1, 3, 5, 7, 9. Следовательно, n = 5, m = 3. По формуле получаем:

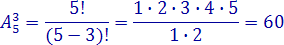
1 3. Имеется 12 ролей. Четыре артиста могут играть любую роль, и всем им предлагается выбор. Сколькими способами можно распределить роли между ними?

Пронумеруем роли: 1, 2, 3, …, 9, A, B,C. Тогда задачу можно переформулировать: сколько существует четырехразрядных чисел, которые могут быть образованы из 12 цифр (без повторов)? Каждое четырех-разрядное число будет соответствовать некоторому выбору ролей, если принять, что первому артисту ставится в соответствие первый разряд, второму – второй, третьему – третий и четвертому – четвертый. Согласно условию имеем n =12, m=4, тогда:

13. Сколько можно образовать четырехразрядных чисел, используя только цифры 3, 7, 8, 9, если повторения возможны?

По правилу произведения на первом месте может находиться любая из четырех цифр, следовательно, имеем 4 случая. Так как повторы разрешены, то на втором месте может находиться любая из четырех заданных цифр – имеем снова 4 случая. Для двух остальных разрядов имеем еще по 4 случая. Таким образом:

14. Сколько всего существует трехразрядных десятичных чисел, которые могут быть составлены из цифр 1, 2, 4, 5, 6, 8?

На месте старшего разряда может находиться одна из цифр 1, 2, 4, 5, 6, 8 – всего их шесть. По шесть цифр могут находиться и в двух младших разрядах. Следовательно:

16. Дано множество букв: А = {а, б, в, г, д, е}. Сколько двух- и трехбуквенных слов.

Искомое число R равно:

17. Сколько существует пятиразрядных чисел шестеричной системы счисления?

Решим эту задачу сначала в общем виде. Пусть n – основание системы счисления, m – длина выборки. Первую цифру можно выбрать n – 1 способами, так как с нуля не могут начинаться m-разрядные числа. Во всех остальных разрядах цифры выбираются n способами каждая. Следовательно, искомое число К m-разрядных чисел равно:

Согласно условию примера m = 5, n = 6, тогда:

18. Сколько существует шестиразрядных двоичных чисел, содержащих три единицы?

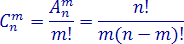
В данном случае n=6, m=3, следовательно, искомое число равно: