
№1 зертханалық жұмыс
Тақырыбы: Санау жүйелері.
Жұмыстың мақсаты: Дербес компьютердің құрылысын, ақпаратты сақтау әдістерін және компьютерде қолданылатын санау жүйелерін меңгеру.
Теориядан қысқаша мағлұматтар
Санау жүйесі
Кез келген позициялық жүйе келесі түрде енгізіледі. р – бүтін саннан тұратын негізі және 0, 1, 2,..., р-1 цифрларынан тұратын алфавит таңдалынады. Сонда осы жүйедегі кез келген Х саны:

қосындысы түрінде ұсынылады. Мұндағы, Х – бүтін бөлігі n+1 цифрдан және бөлшек бөлігі k цифрдан тұратын, негізі p болатын жүйедегі сан. Ал, ai – жүйе алфавитіндегі сандар. Ендеше, жүйеде берілген сандарды жазу келесі түрде болады:
Xp=an an-1…a1 a0 , a-1…a-k .
Ондық позициялық санау жүйесінде санды жазу үшін он цифр қолданылады: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Бұл жүйедегі кез келген сан мына түрде жазылады:
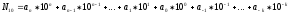
Компьютерде әдетте екілік санау жүйесі, яғни 2 негіздеуші бар санау жүйесі қолданылады. Екілік жүйеде кез келген сан 0 мен1 цифрларының көмегімен жазылады және екілік сан деп аталады. Екілік санау жүйесіндегі санның жазылу түрі:

Екілік жүйенің елеулі кемшілігі – мұнда санды жазу үшін 0 және 1 цифрлары көп қажет болады. Бұл адамның екілік санды қабылдауын қиындатады. Сондықтан екілік жүйе әдетте компьютердің «ішкі қажеттілігі» үшін қолданылады, ал адамның компьютермен жұмыс істеуі үшін үлкен негіздеуішті санау жүйесі таңдалады. Бұл кезде сегіздік немесе он алтылық жүйелер жиі қолданылады.
Сегіздік санау жүйесі сегіз цифрдың көмегімен санды көрсетеді: 0, 1, 2, 3, 4, 5, 6, 7.
16 негіздеушісі бар санау жүйесін он алтылық санау жүйесі деп атайды. Он алтылық позициялық санау жүйесінде санды жазу үшін ондық санау жүйесінің цифрлары 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 және жетпейтін алты цифрды белгілеу үшін ондық сандардың мәні 10, 11, 12, 13, 14 және 15 болатын сәйкес латын алфавитінің алғашқы үлкен әріптері: A, B, C, D, E, F қолданылады. Сонда он алтылық жүйенің барлық цифрлары мыналар: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Ондық санау жүйесіндегідей, сегіздік және он алтылық санау жүйелеріндегі сандар оңай оқылады, олар екілік санау жүйесіне қарағанда сәйкесінше үш (сегіздік) және төрт (он алтылық) есе аз разрядты қажет етеді (8 және 16 сандары 2 санының сәйкесінше үшінші және төртінші дәрежесі).
Сегіздік және он алтылық сандарды екілік жүйеге ауыстыру өте қарапайым: әрбір цифрды оған эквивалентті екілік триадамен (үш цифрмен) немесе тетрадамен (төрт цифрмен) алмастыру керек.
Мысалы:

Санды екілік жүйеден сегіздік немесе он алтылық жүйеге ауыстыру үшін, оны үтірден солға және оңға қарай триадаға (сегіздік үшін) немесе тетрадаға (он алтылық үшін) бөлу керек және әр топты сәйкесінше сегіздік (он алтылық) цифрлармен алмастыру керек.
Мысалы,
Сандарды жазу жүйелері
|
10-дық 2-лік 8-дік 16-лық 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D
4 1110
6 E 15 1111 17 F 16 10000 20 10
|
Сандарды р санау жүйесінен ондық санау жүйесіне ауыстыру
Сандарды р санау жүйесінен ондық санау жүйесіне ауыстыру үшін, осы жүйедегі санды:

қосындысы түрінде жазып, ондық жүйенің ережесі бойынша арифметикалық операцияларды орындау керек.
1-Мысал: 1010101,101 екілік саны үшін қосынды мына түрде болады:
1010101,101=1*26+0*25+1*24+0*23+1*22+0*21+1*20+1*2 -1+0*2 -2+1*2-3
Осы қосындыда арифметикалық операцияларды орындай отырып, 85,625 санын аламыз. Осылайша 1010101,101 екілік саны 85,625 ондық санына сәйкес келеді. Яғни:
Жауабы: 1010101,1012 = 85,62510.
2-Мысал: 357 сегіздік санын ондық санау жүйесіне ауыстырайық.
3578 = 3*82+5*81+7*80 = 23910.
Жауабы: 3578 = 23910
3-Мысал: 3Е5А1 он алтылық санын ондық санау жүйесіне ауыстырайық .
3Е5А116 = 3*164+E*163+5*162+A*161+1*160
Ондық жүйенің ережесі бойынша арифметикалық операцияларды орындай отырып және А=10, Е=14 екенін ескере отырып аламыз:
Жауабы: 3Е5А116 = 25539310.
Сандарды ондық санау жүйесінен р санау жүйесіне ауыстыру
А) 1-ереже (Бүтін ондық сандарды р санау жүйесіне ауыстыру ережесі):
Бүтін ондық санды р санау жүйесіне ауыстыру үшін осы санды қалдықтарын белгілеп ала отырып, бөлінді бөлгіштен кіші болғанша р-ға бөле беру керек. Нәтижесінде қалған бөліндіден бастап, оңнан солға қарай қалдықтарды бір қатарға жаза отырып, ондық санның р санау жүйесінде жазылу түрін аламыз.
Мысалы, ондық санау жүйесіндегі 75 санын екілік, сегіздік, он алтылық санау жүйелеріне ауыстырайық.


Жауабы: 7510 = 1 001 0112 = 1138 = 4B16.
Ә) 2-ереже (Ондық бөлшек санды р санау жүйесіне ауыстыру ережесі):
Ондық бөлшек сандарды р санау жүйесіне ауыстыру үшін осы бөлшекті р-ға көбейту керек. Алынған көбейтіндінің бүтін бөлігі бөліп алынады, бөлшек бөлігі тағы да р-ға көбейтіледі. Осылайша бөлшек бөлігінде 0 шыққанша немесе периоды анықталғанша, бүтін бөлігін бөліп ала отырып р-ға көбейте береміз. Нәтижесінде бүтін бөлігін солдан оңға қарай бір қатарға жаза отырып, бөлшек санның р санау жүйесінде жазылу түрін аламыз.
Мысалдар қарастырайық.
4-мысал: 0,6875 бөлшегін екілік санау жүйесіне ауыстырайық.
0,6875 0,375 0,75 0,5
 2
2 2 2
2
2 2 2


 1,3750
0,750 1,50 1,0
1,3750
0,750 1,50 1,0
Жауабы: 0,687510 = 0,10112
Ақырғы ондық бөлшекті екілік санау жүйесіне ауыстырған кезде периодты бөлшек алынуы мүмкін.
5-мысал: 0,3 ондық бөлшегін екілік санау жүйесіне келтіреміз:
0,3*2=0,6
0,6*2=1,2
0,2*2=0,4
0,4*2=0,8
0,8*2=1,6
0,6*2=1,2
0,6 бөлшек бөлік есептеудің екінші қатарында болған еді. Сондықтан есептеулер қайталана бастайды. Демек, екілік санау жүйесінде 0,3 периодты бөлшек түрінде ұсынылады. 0,310 =0,0(1001)2
6-мысал: 0,121 санын он алтылық санау жүйесіне ауыстырайық.
0,121 0,936 0,976 0,616 0,856 0,696





 16
16 16 16 16 16
16
16 16 16 16 16
0726 5616 5856 3696 5136 4176





 0121 936
976 616 856 696
0121 936
976 616 856 696
1,936 14,976 15,616 9,856 13,696 11,136
Жауабы: 0,12110 = 0,1ЕF9DB...
Б) 3-ереже (Аралас санды р санау жүйесіне ауыстыру ережесі):
Аралас санды р санау жүйесіне ауыстыру үшін, осы санның бүтін бөлігі жеке, бөлшек бөлігі жеке ереже бойынша ауыстырылады. Содан кейін алынған нәтижелер үтір арқылы бірге жазылады.
7-мысал: 123,1875 санын сегіздік санау жүйесіне ауыстырайық:
123:8=15(3) 0,1875*8=1,5
15:8=1(1) 1,5*8=4,0 123,187510=173,148
1:8=0(1) 0,1875=148
123=1738
