
- •1.2 Описание работы машины
- •2.2 Структурный анализ кулачкового механизма
- •3.2 Определение скоростей точек и звеньев механизма
- •3.3 Определение ускорений точек и звеньев механизма
- •5.3 Картины линейных и угловых скоростей зубчатого механизма
- •Выбирается ордината графика аналога ускорений на фазе удаления
- •6.3 Профилирование кулачка
3.3 Определение ускорений точек и звеньев механизма
Найдем ускорение точки A:

Так
как
 , а
, а
 , тогда
, тогда
 .
Отсюда ускорение точки a
:
.
Отсюда ускорение точки a
:

Направим
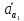 параллельноO1A.
параллельноO1A.
На
плане ускорений для заданного положения
механизма изобразим ускорение точки A
отрезком
 ,
тогда масштабный коэффициент плана
ускорений будет равен:
,
тогда масштабный коэффициент плана
ускорений будет равен:

Найдем ускорение точки A3:

Величину
ускорения
 можно
вычислить:
можно
вычислить:
 мс-2.
мс-2.
Находим отрезок
 мм,
мм,
изображающий
на плане ускорение
 ,
отрезок
,
отрезок
 пристраиваем к точке a
перпендикулярно OA,
через точку k
проводим линию действия ускорения
пристраиваем к точке a
перпендикулярно OA,
через точку k
проводим линию действия ускорения
 -
параллельно к OA.
-
параллельно к OA.
Ускорение
 можно вычислить
можно вычислить

Находим
отрезок


изображающий
на плане ускорений ускорение
 .
Через полюс π
проводим линию, параллельную A3O2,
и в направлении от A3
к O2
откладываем отрезок πn3,
затем через точку n3
проводим линию действия ускорения
.
Через полюс π
проводим линию, параллельную A3O2,
и в направлении от A3
к O2
откладываем отрезок πn3,
затем через точку n3
проводим линию действия ускорения
 -
перпендикулярно к A3O2.
Точка пересечения линий действия
-
перпендикулярно к A3O2.
Точка пересечения линий действия
 и
и
 -
дает точку a3
– конец вектора πa3,
определяющего на плане ускорений
ускорение
-
дает точку a3
– конец вектора πa3,
определяющего на плане ускорений
ускорение
 .
Величина ускорения
.
Величина ускорения
 мс-2
мс-2
Ускорение точки B находим по теореме подобия:
 мм.
мм.
Отрезок πb, направленный по линии πa3, определит ускорение точки B. Величина ускорения
 мс-2.
мс-2.
Определяем далее ускорение точки C:

Величина
ускорения
 вычисляется по формуле:
вычисляется по формуле:

От точки b на плане ускорений откладываем отрезок
 мм.
мм.
Затем
через точку n4
проводим линию действия ускорения
 .
Ускорение точки C
относительно направляющей ползуна
направлено параллельно направляющей.
На основании этого через полюс π
проводим линию действия ускорения aC'.
Точка пересечения линий действия
.
Ускорение точки C
относительно направляющей ползуна
направлено параллельно направляющей.
На основании этого через полюс π
проводим линию действия ускорения aC'.
Точка пересечения линий действия
 и
и
 определяет
на плане ускорений точку c
– конец отрезка πc,
изображающего ускорение точки C.
Величина ускорения
определяет
на плане ускорений точку c
– конец отрезка πc,
изображающего ускорение точки C.
Величина ускорения
 [мс-2].
[мс-2].
Угловое ускорение звена 3:
 =0,02с-2,
=0,02с-2,
Направление ε2 по часовой стрелке.
Угловое ускорение звена 4:
 2,68с-2,
2,68с-2,
Направление ε4 против часовой стрелки.
4. Силовой анализ рычажного механизма
Определение инерционной нагрузки
Зная массу звеньев, найдем вес звеньев:




Силы инерции:


Моменты инерции:


4.1 Силовой расчет группы Ассура 4-5
На плане силового расчета группы Ассура 4-5 показана структурная группа, состоящая из звеньев 4,5 с учетом масштабного коэффициента длин
 .
.
Запишем уравнение равновесия сил структурной группы

Составим уравнение моментов относительно точки C для звена 4:




Строим
план сил структурной группы с учетом
масштабного коэффициента
 .
.
Определяем отрезки, изображающие на плане сил:





После построения плана сил определяем реакции:



4.2 Силовой расчет группы Ассура 2-3
Запишем уравнение равновесия сил структурной группы

Составим уравнение моментов относительно точки O2:




Строим
план сил структурной группы с учетом
масштабного коэффициента
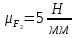 .
.
Определяем отрезки, изображающие на плане сил:



После построения плана сил определяем реакции:



4.3 Силовой расчет начального звена
Запишем уравнение равновесия сил начального звена:

Построим
план сил начального звена с учетом
масштабного коэффициента .
.
Отрезки, изображающие силы на плане сил:


После построения плана сил найдем реакции:



Величину и направление уравновешивающего момента MУР определяем из уравнения моментов сил относительно точки О1:


Отсюда:

5. Синтез зубчатого механизма
5.1 Синтез простой передачи
Расчет основных геометрических параметров
Дополнительные исходные данные:
Нормальный исходный контур
Угол главного профиля α=20°
Коэффициент высоты головки зуба h*α=1,0
Коэффициент радиального зазора с*=0,25
Коэффициент радиуса кривизны переходной кривой ρ*f=0,38
Колеса цилиндрические, угол наклона зуба β=0°
Коэффициент смещения шестерни х1=0,5, колеса х2=0.
Z7=12
Z8=36
Модуль простой передачи m=5 мм
Расчет основных геометрических параметров
-
Делительное межосевое расстояние
α = m * (z7+ z8) / 2 * cosβ = 5 * (12+36)/2 = 120 мм
2) Коэффициент суммы смещений
X∑ = x1 + x2 = 0,5 + 0 = 0,5 мм
3)Угол профиля

4)Угол зацепления
invαtw =(2 * X∑ * tgαt/ z7+ z8 ) + invαt=(2*0.5*0.3693 / 12+36)+ 0.0149 = 0.0224
По таблице invαt = 0,0149, αtw = 22,800
5)Делительный диаметр
-шестерни d7=(z7 * m) / cosβ =(12 * 5) / 1 = 60 мм
-колеса d8=(z8* m) / cosβ =(36* 5) / 1 = 180 мм
6) Межосевое расстояние
αw = ((z7+ z8) * m * cosαt)/ 2 * cosβ * cosαtw= ((12+36) * 5 * 0,9396) / 2 * 1 * 0,92 = 122,5 мм
7) Передаточное число
i = z8/ z7=36 / 12 = 3
8) Начальный диаметр
-шестерни dW7 = (2 * αw)/ (i + 1) = 2 * 122,5 / 4 = 61, 25 мм
-колеса dW8=( 2 * αw * i)/ (i + 1) = 2 * 122,5 * 3 / 4 = 183,75мм
9) Коэффициент воспринимаемого смещения
у = (αw – α) / m = (122,5 – 120) / 5 = 0,5
10) Коэффициент уравнительного смещения
∆y= X∑ - y = 0,5 – 0,5 = 0 мм
11) Диаметр вершин зубьев
-шестерни da7 = d7 + 2*(h*a+ x1-∆y)*m=60+2*(1+0,5-0)*5=75 мм
-колеса da8 = d8 + 2*(h*a + x2-∆y)*m = 180 + 2*(1+ 0 -0)*5 =190 мм
12) Диаметр впадин
-шестерни df7 = d7 - 2*(h*a+c* -x1)*m = 60 - 2*(1+0,25-0,5)*5 = 52,5 мм
-колеса df8 = d8 - 2*(h*a+c* -x2)*m = 180 - 2*(1+0,25-0)*5 = 167,5 мм
13) Высота зуба
-шестерни h7 = 0,5 * (da7- df7 )=0,5*(75 - 52,5) = 11,25 мм
-колеса h8 = 0,5 * (da8- df8 )=0,5*(190 – 167,5) = 11,25мм
14) Основной диаметр
-шестерни db7 = d7 * cosαt= 60 * 0,9396 = 56,37 мм
-колеса db8 = d8 * cosαt= 180 * 0,9396 = 169,12 мм
15) Расчетный шаг
P = * m = 3,14 * 5 = 15,7мм
16) Шаг зацепления
Pa = * m * cosαtw= 3,14 * 5 * 0,9218 = 14,47 мм
17) Толщина зуба по делительной окружности
-шестерни S7 = P/2 + 2*x1*m* tgαt = 15,7/2 + 2*0,5*5*0,3639 =9,66 мм
-колеса S8 = P/2 + 2*x2* m* tgαt = 15,7/2 + 2*0*5*0,3639 =7,85 мм
18) Коэффициент перекрытия
α = ga / Pa= 16,4 / 14,47 = 11,33 мм
Угловой шаг
7= 2 /z7= 300 ; 8= 2 / z8= 100
Рассчитав все величины черчу внешнее эвольвентное зацепление в масштабе 5:1.
5.2 Синтез планетарного редуктора
Выбор чисел зубьев колес:
-
Определяем требуемое передаточное отношение механизма:

где
 -
передаточное отношение
-
передаточное отношение

 -
передаточное отношение рядового
механизма
-
передаточное отношение рядового
механизма

Отсюда,

-
Из условия отсутствия подрезания зубьев z1=z3>17 делаем подбор зубьев:
Принимаем
z1=z3=18.
По уравнению определяем
 :
:

где -
передаточное отношение планетарного
механизма, так как
-
передаточное отношение планетарного
механизма, так как

Отсюда
получим равным
равным
 .
.
По
условию соосности определяем


Проверяем условие соседства:
-для системы колес внешнего зацепления

где k- число блочных сателлитов

-для системы колес внутреннего зацепления


Условия соседства выполняются.
Проверяем условие отсутствия заклинивания по таблице 2:
для
колес внешнего зацепленияz1=18,
при, - любое, условие выполняется;
- любое, условие выполняется;
для
колес внутреннего зацепления, при ,
, , условие не выполняется.
, условие не выполняется.
Принимаем
z1=z3=19,
тогда
 ,
, .
.
Проверяем условие соседства:
-для системы колес внешнего зацепления

-для системы колес внутреннего зацепления

Условия соседства выполняются.
Проверяем условие отсутствия заклинивания по таблице 2:
для
колес внешнего зацепления z1=19,
при, - любое, условие выполняется;
- любое, условие выполняется;
для
колес внутреннего зацепления, при ,
, , условие не выполняется.
, условие не выполняется.
Принимаем
z1=z3=20,
тогда
 ,
,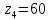 .
.
Проверяем условие соседства:
-для системы колес внешнего зацепления

-для системы колес внутреннего зацепления

Условия соседства выполняются.
Проверяем условие отсутствия заклинивания по таблице 2:
для
колес внешнего зацепления z1=20,
при, - любое, условие выполняется;
- любое, условие выполняется;
для
колес внутреннего зацепления, при ,
, ,
условие не выполняется.
,
условие не выполняется.
Принимаем
z1=z3=21,
тогда
 ,
, .
.
Проверяем условие соседства:
-для системы колес внешнего зацепления

-для системы колес внутреннего зацепления

Условия соседства выполняются.
Проверяем условие отсутствия заклинивания по таблице 2:
для
колес внешнего зацепления z1=21,
при, - любое, условие выполняется;
- любое, условие выполняется;
для
колес внутреннего зацепления, при ,
, ,
условие выполняется.
,
условие выполняется.
Проверяем условие сборки:

где n – число полных оборотов водила;
k– число блочных сателлитов;
 – целое
положительное число.
– целое
положительное число.
Число
nподбирается
с таким расчетом, чтобы значение
 получилось целым (n
=1, 2, 3 …).
получилось целым (n
=1, 2, 3 …).

Отсюда
 .
.
