3. Методы параметрической оптимизации динамических систем

Изобразим область настроечных параметров ПИ регулятора в декартовой системе координат (рисунок 5) в виде прямоугольника БСДО. Предположим, что в области БСДО есть значения настроечных параметров при которых квадратичный критерий качества отличается от значения в базовой точке А. В общем случае таких комбинаций настроечных параметров может быть несколько, т.е. область БДСО может иметь много локальных минимумов критерия J₂. Для локализации областей с минимальными значениями J₂ предлагается воспользоваться методом сеток: разбить прямоугольник сеткой, например 4х4, как показано на рисунке 5. Далее предлагается провести в каждом узле полученной сетки имитационные эксперименты по моделированию САР с фиксированием переходных процессов и значений интегральных квадратичных критериев качества. Точки сетки в которой САР не устойчива, из анализа исключаются. Среди оставшихся следует выбрать комбинации {К_р, Т_и}, для которых получены минимальные значения J₂.

Рисунок 5. Область настроечных параметра

На этом первую версию экспериментов локализации локальных минимумов областей настроечных параметров САР можно считать законченной.

Существуют другие методы многомерной параметрической оптимизации, в том числе:

• метод Гаусса-Зейделя (метод координатного подъема);

• метод случайного поиска;

• симплексный метод;

• градиентные методы (например, метод планирования факторных экспериментов и крутого восхождения в направлении антиградиента функции цели).

В [2, 3] описываются алгоритмы перечисленных методов, а так же приводятся характеристики области их применения.

В настоящей лабораторной работе предлагается после проведения первой серии экспериментов, описанной выше, воспользоваться^)*)* имеющейся в ППП MVTU компонентой "Оптимизация параметров САР", при этом исходной точкой параметрической оптимизации САР следует взять один из локальных минимумов, полученный в первой серии имитационных экспериментов с помощью метода сеток.

4. Содержание отчета по лабораторной работе

В отчет по лабораторной работе должна входить следующая информация:

1. Исходные данные в соответствии с заданным вариантом из таблицы 2.

2. Функциональная схема САР.

3. Схема программного аналога САР на средствах ППП MVTU.

4. Результаты имитационного моделирования САР в базовой точке (т.е. когда Кр= и Ти=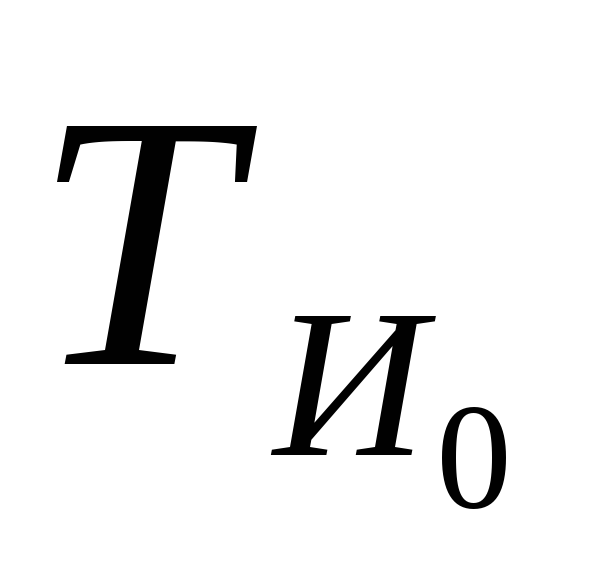) в виде переходного процесса у(t) при f(t) = Мн1(t-), Q(t)=Qз(t), значении J₂.

5. Результаты поисковых экспериментов, улучшающих J₂ (не менее, чем для 5-ти экспериментов в области настроечных параметров регулятора).

Примечание. При решении задачи параметрической оптимизации средствами ППП MVTU объем отчета студент должен согласовать с преподавателем.

1. Список контрольных вопросов

1. Сформулируйте задачи параметрической оптимизации САР.

2. Какие критерии качества САР, кроме интегральной квадратичной оценки, могут использоваться для параметрической оптимизации САР?

3. Как в ППП MVTU можно определить момент окончания переходного процесса?

4. Как в ППП MVTU можно определить значение интегральной квадратичной оценки?

5. Сформулируйте алгоритм метода координатного подъема.

6. Сформулируйте алгоритм симплексного поиска.

7. Сформулируйте алгоритм метода случайного поиска.

Примечание. Вопросы 5, 6 и 7 могут быть изучены по [2, 3].