
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«СЕВЕРО-ЗАПАДНЫЙ ГОСУДАРСТВЕННЫЙ ЗАОЧНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра информатики и прикладной математики
МАТЕМАТИКА
ЧИСЛЕННЫЕ МЕТОДЫ
РАБОЧАЯ ТЕТРАДЬ
для выполнения контрольной и лабораторных работ
Институты: все Укрупненные группы специальностей и направлений подготовки высшего
профессионального образования: 080000 – Экономика и управление
140000 – Энергетика, энергетическое машиностроение и электротехника
150000 – Металлургия, машиностроение и материалообработка
190000 – Транспортные средства
200000 – Приборостроение и оптотехника
210000 – Электронная техника, радиотехника и связь
220000 – Автоматика и управление
230000 – Информатика и вычислительная техника
240000 – Химия и биотехнологии
260000 – Технология продовольственных продуктов и потребительских товаров
280000 – Безопасность жизнедеятельности, природообустройство и защита окружающей среды
Санкт-Петербург Издательство СЗТУ
2009
Утверждено редакционно-издательским советом университета
УДК 519.95
Математика. Численные методы. Рабочая тетрадь для выполнения контрольной и лабораторных работ. – СПб.: Изд-во СЗТУ, 2009. – 70 с.
Методическое издание, представленное в виде рабочей тетради, разработано на основании государственных образовательных стандартов высшего профессионального образования.
Рабочая тетрадь является вспомогательным материалом при выполнении контрольной и лабораторных работ. Содержится справочный материал в виде
конспекта-справочника одного из разделов математики – численные методы: методов интерполяции (формулы Ньютона, Лагранжа), численного вычисления определенного интеграла, решения дифференциального уравнения (метод Эйлера), приближенного решения алгебраических уравнений (метод Ньютона, метод половинного деления), знание которых проверяется в контрольной работе. Рассмотрено подробное решение примеров по перечисленным темам, представлена методика реализации их решения в Excel, освобождающая от выполнения рутинных вычислений. Приведены условия репетиционных примеров, которые предлагается студентам сделать, прежде чем приступить к выполнению контрольной работы. В конце тетради приводятся ответы. Даются задания для выполнения контрольной и лабораторных работ. Для экономии времени представлены шаблоны таблиц, в которых можно осуществлять решение.
Рассмотрено на заседании кафедры информатики и прикладной математики 11.06.2008. Одобрено методической комиссией факультета общепрофессиональной подготовки 24.06.2008.
Рецензенты: кафедра информатики СЗТУ (зав. кафедрой Г.Г. Ткаченко, канд. физ.-мат. наук, доц., Л.В. Боброва, канд. техн. наук, проф.); Ю.Н. Сидоров, канд. техн. наук, доц. кафедры математического обеспечения и применения ЭВМ СПбГЭТУ (ЛЭТИ).
Составитель Н.М. Петухова, канд. техн. наук, доц.
© Северо-Западный государственный заочный технический университет, 2009
Предисловие
Рабочая тетрадь предназначена для самостоятельной работы студентов второго курса по изучению одного из разделов математики – численных методов. В тетради приводится краткий конспект тех численных методов, которые вошли в контрольную работу – методов интерполяции, численного вычисления определенного интеграла, приближенного решения дифференциального уравнения методом Эйлера, численного решения алгебраических уравнений (методом касательных, половинного деления). Подробно описывается решение типовых примеров, которые студенты должны выполнить в контрольной работе, представлена методика реализации их решения в Excel. Приведены условия репетиционных примеров, которые рекомендуется выполнить студентам, прежде, чем приступать к решению контрольной работы.
Целесообразно сначала разобраться с решением демонстрационных примеров, затем реализовать их расчет в Excel по образцу, представленному в тетради, внимательно ознакомиться с таблицами, представленными в режиме формул, так как они помогут лучше понять алгоритм вычислений. Для экономии времени даются шаблоны таблиц, в которых целесообразно выполнять вычисления. Проверить правильность решения репетиционных примеров помогут ответы, приведенные в конце рабочей тетради.
Рабочая тетрадь позволит с наименьшими затратами времени освоить представленный материал, успешно выполнить контрольную и лабораторные работы.
1. Интерполяция функций с помощью формул Ньютона
1.1. Постановка задачи
Пусть некоторая функция y = f(x) задана таблицей, т.е. для (n + 1)-го значения аргумента x известны (n + 1) значения функции y = f(x) (табл.1.1).
|
|
|
Таблица 1.1 |
||
x |
x0 |
x1 |
… |
xn |
|
f(x) |
f(x0) |
f(x1) |
|
f(xn) |
|
Задача интерполяции заключается в замене функции y = f(x), аналитическое выражение которой неизвестно, другой функцией F(x), аналитическое выражение которой известно. Это дает возможность вычислять значения функции f(x) в точках, отличных от значений аргументов, фиксированных в таблице. При этом необходимо найти такое аналитическое выражение заданной функции f(x), т. е. функцию F(x), значения которой будут совпадать с табличными значениями функции y = f(x) для заданных значений аргументов x0, x1, …, xn:
F(x0) = f(x0) = y0, |
|
F(x1) = f(x1) = y1, |
|
………………… |
(1.1) |
F(xn) = f(xn) = yn.
Функция F(x) называется интерполирующей функцией, точки x0, x1, …, xn – узлами интерполяции (узловыми точками), а задача нахождения функции F(x) – задачей интерполяции. Величина h = xk - xk-1 называется шагом интерполяции. Шаг интерполяции может быть постоянным или переменным.
В некоторых случаях бывает необходимо строить функцию F(x) для функции y = f(x), аналитическое выражение которой известно, но является слишком сложным и неудобным для дальнейшего использования.
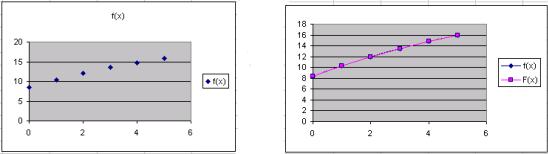
Геометрически задача интерполирования означает построение кривой, проходящей через точки плоскости с координатами (xi, yi) (рис. 1.1). Чаще всего в качестве интерполирующей функции F(x) используются многочлены
Pn(x) = a0xn + a1xn-1 + … + an-1x + an |
(1.2) |
В этом случае задача интерполяции состоит в подборе многочлена n- й степени Pn(x), значения которого в узлах интерполяции совпадают со значениями интерполируемой функции y = f(x):
y0 = f(x0) = Pn(x0), |
|
y1 = f(x1) = Pn(x1), |
(1.3) |
………………… |
|
yn = f(xn) = Pn(xn)
и сводится к вычислению коэффициентов a0, a1, …, an интерполяционного многочлена. Доказано, что существует единственный интерполяционный многочлен n-ой степени, удовлетворяющий условиям (1.3).
Рис. 1.1
1.2. Конечные разности
Чаще всего для интерполяции функций с равноотстоящими узлами используются интерполяционные многочлены Ньютона. Для их записи используют конечные разности функций.
Пусть для значений аргументов x0, x1, …, xn заданы значения функции y
= f(x): y0 = f(x0), y1 = f(x1), …, yn = f(xn), причем x1 - x0 = x2 - x1=…= xn – xn-1 = h (табл. 1.2).
|
|
|
|
Таблица 1.2 |
|
x |
x0 |
x0 + |
x0 + 2h |
… |
x0 + |
|
|
h |
|
|
nh |
y |
y0 |
y1 |
y2 |
|
yn |
Конечной разностью первого порядка называется разность между значе-
ниями функции в соседних узлах интерполяции: yi = yi+1 - yi, i = 0, 1, …, n-1, т.е.
y0 = у1 – y0, y1 = у2 – y1,
……………. |
(1.4) |
yn-1 = уn – yn-1.
По первым конечным разностям можно найти конечные разности второго
порядка:
2y0 = у1 – y0 = y2 - 2y1 + y0,
2y1 = у2 – |
y1 = y3 - 2y2 + y1, |
(1.5) |
……………............................, |
|
|
2yn-1 = уn – yn-1 = yn - 2yn-1 + yn-2. |
||
В общем виде конечная разность k-го порядка |
|
|
kyi = |
k-1уi+1 – k-1yi. |
(1.6) |
Вычисление конечных разностей удобно выполнять в таблице (табл. 1.3).
Таблица 1.3
|
|
|
|
|
|
|
xi |
yi |
yi |
2yi |
3yi |
4yi |
5yi |
x0 |
y0 |
y0 |
2y0 |
3y0 |
4y0 |
5y0 |
x1 |
y1 |
y1 |
2y1 |
3y1 |
4y1 |
… |
x2 |
y2 |
y2 |
2y2 |
3y2 |
… |
|
x3 |
y3 |
y3 |
2y3 |
… |
|
|
x4 |
y4 |
y4 |
… |
|
|
|
x5 |
y5 |
… |
|
|
|
|
… |
… |
|
|
|
|
|
Для проверки правильности вычислений конечных разностей удобно использовать их свойство: сумма чисел в каждом столбце разностей равна разности крайних членов предыдущего столбца. Сумма всех разностей первого порядка определяется следующим образом:
n 1 |
n 1 |
n 1 |
n 1 |
yi ( yi 1 |
yi ) yi 1 |
yi yn y0 . (1.7) |
|
i 0 |
i 0 |
i 0 |
i 0 |
Например, для n = 5: ( y1 + y2 + y3 + y4 + y5) – (y0 + y1 + y2 + y3 + y4) = y5 - y0.
Аналогично, для разностей других порядков будем иметь:
n 1 |
|
|
k yi ynk k1 |
1 k 1 y0 . |
(1.8) |
i 0
Пример 1.1. Функция y = f(x) задана таблицей (табл. 1.4). Вычислить конечные разности функции y = f(x). Проверить правильность вычислений, используя описанное выше свойство.
|
Таблица 1.4 |
|
xi |
yi |
|
0 |
8,5 |
|
1 |
10,5 |
|
2 |
12,0 |
|
3 |
13,5 |
|
4 |
14,5 |
|
5 |
15,5 |
|
Решение. Вычисление конечных разностей и проверку правильности их вычислений удобно выполнять в таблице (табл. 1.5).
Таблица 1.5
i |
xi |
yi |
yi |
2yi |
3yi |
4yi |
5yi |
|
|
|
|
|
|
- |
|
0 |
0 |
8,5 |
2,0 |
-0,5 |
0,5 |
1,0 |
2,0 |
|
|
|
|
|
- |
|
|
1 |
1 |
10,5 |
1,5 |
0,0 |
0,5 |
1,0 |
|
2 |
2 |
12,0 |
1,5 |
-0,5 |
0,5 |
|
|
3 |
3 |
13,5 |
1,0 |
0,0 |
|
|
|
4 |
4 |
14,5 |
1,0 |
|
|
|
|
5 |
5 |
15,5 |
|
|
|
|
|
|
∑ |
|
7,0 |
-1,0 |
0,5 |
0,0 |
2,0 |
|
yn-y0 |
7,0 |
-1,0 |
0,5 |
0,0 |
2,0 |
|
1.3.Первая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции
Вычисление значений функции для значений аргументов, лежащих в начале таблицы, удобно проводить, пользуясь первой интерполяционной формулой Ньютона. В этом случае интерполяционный многочлен представляют в виде:
F(x) = Pn(x) = a0 + a1(x – x0) + a2(x –x0)(x – x1) +
+ a3(x –x0)(x- x1)(x-x2) + ... + an(x –x0)(x- x1)(x-x2)…(x –xn-1), (1.9)
при этом неизвестные значения коэффициентов a0, a1, a2, …, an вычисляют по
формуле |
|
|
|
ai |
i y0 |
(i = 0, 1, 2, …, n), |
(1.10) |
|
i!hi |
|
|
то есть
при i = 0 |
a0 |
|
0 y00 |
|
y0 |
|
, [0!=1, |
0y0 = y0], |
|
||||
|
|
|
|||||||||||
|
|
|
0!h |
|
|
1 |
|
|
|
|
|
|
|
при i = 1 |
a1 |
|
1 y10 |
= |
|
y0 |
, |
|
|
|
|
||
|
|
|
1!h |
|
|
|
|
h |
|
|
|
|
|
при i = 2 |
a2 |
|
2 y0 |
= |
2 y20 |
, и т. д. |
|
|
|
||||
|
|
|
2!h 2 |
|
|
2!h |
|
|
|
|
|
||
Обратите внимание, что a i 1 |
|
|
i 1 y 0 |
1 |
|
1 |
. (1.11) |
||||||
|
i 1 |
(i 1) h |
|||||||||||
|
|
|
|
|
|
|
|
|
|
i! h |
|
|
|
После подстановки найденных коэффициентов ai в выражение (1.9), получают первую интерполяционную формулу Ньютона:
F (x) y |
0 |
y0 (x x |
0 |
) 2 y0 |
(x x |
0 |
)(x x ) |
3 y0 (x x |
0 |
)(x x )(x x |
2 |
) ... |
||||
|
|
h |
2!h2 |
|
1 |
3!h3 |
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
n y0 (x |
x |
0 |
)(x x )(x x |
2 |
)...(x x |
n |
). |
|
|
(1.12) |
||||||
n!hn |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1.1 (продолжение). Используя первую интерполяционную формулу Ньютона, построить интерполяционный многочлен для функции, заданной таблицей (табл. 1.4). Найти значение этой функции для x = 2,5.
Решение. Для функции, заданной табл. 1.4, конечные разности были построены (см. табл. 1.5). Используя ее, построим интерполяционный многочлен по формуле Ньютона (1.12). Так как степень интерполяционного многочлена определяется порядком конечных разностей, интерполяционный многочлен для рассматриваемого примера будет иметь вид (1.13).
Для вычисления разностей x-xi введем в табл. 1.5 дополнительный столбец
(табл. 1.5-а).
Таблица 1.5-а
|
|
|
|
2yi |
3yi |
4yi |
5yi |
x- |
i |
xi |
yi |
yi |
xi |
||||
|
|
|
|
|
|
- |
2,0 |
|
0 |
0 |
8,5 |
2,0 |
-0,5 |
0,5 |
1,0 |
|
2,5 |
|
|
|
|
|
- |
|
|
|
1 |
1 |
10,5 |
1,5 |
0,0 |
0,5 |
1,0 |
|
1,5 |
2 |
2 |
12,0 |
1,5 |
-0,5 |
0,5 |
|
|
0,5 |
|
|
|
|
|
|
|
|
- |
3 |
3 |
13,5 |
1,0 |
0,0 |
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
4 |
|
4 |
|
|
|
14,5 |
|
|
|
|
|
|
|
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
5 |
|
5 |
|
|
|
15,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
||||||||
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7,0 |
|
|
|
|
|
|
|
-1,0 |
|
|
|
|
|
|
|
|
0,5 |
|
|
0,0 |
|
2,0 |
|
|
||||||||
|
|
|
yn-y0 |
|
|
|
7,0 |
|
|
|
|
|
|
|
|
-1,0 |
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
0,0 |
|
|
2,0 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим коэффициенты интерполяционной формулы (1.13): |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
i = 0 |
a0 |
|
|
|
y0 |
8,5, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
i = 1 |
a1 1 y0 |
|
|
|
|
|
2 |
|
|
|
2 1 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
1!h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1! 1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0,25, |
|
|
|
|||||||||||||||||
|
i = 2 |
a2 2 y0 |
|
1 |
|
|
|
|
2 y0 |
|
|
|
|
|
0,5 1 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
2!h |
2 |
|
|
|
2h |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1!h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
i = 3 |
a3 |
|
3 y0 |
|
|
|
1 |
|
|
|
3 y0 |
|
|
|
|
1 |
|
|
1 |
|
0,5 1 |
|
1 |
0,08, |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
3!h3 |
|
2!h2 |
|
3h |
3 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
I = 4 |
a4 |
4 y0 |
|
|
|
1 |
|
|
|
4 y0 |
1 |
|
|
|
1 |
1 |
1 |
|
1 0,04, |
|||||||||||||||||||||||||||||||||
|
|
|
|
4!h4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3!h3 |
|
|
|
|
|
6 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4h |
|
|
|
4 |
|
|
|
|
|||||||||||||||
|
|
|
i = 5 |
a5 |
|
5 y0 |
|
|
1 |
|
= 5 y0 |
|
|
|
1 |
|
|
|
|
|
1 |
|
2 |
1 |
1 0,02. |
||||||||||||||||||||||||||||||
|
|
|
|
5!h |
5 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
4!h3 |
|
|
5h |
24 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
||||||||||||||
|
Обратите внимание, что для вычисления |
|
|
|
|
|
|
1 |
|
|
|
удобно использовать со- |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
(i 1)!hi 1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
отношение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(i 1)! h i 1 |
|
i! h i |
|
|
(i 1) h |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Данные вычисления целесообразно выполнять в таблице (табл. 1.6). В этой таблице целесообразно производить и вычисление значения функции для задан-
ного значения x.
Таблица 1.6
|
|
|
|
|
|
h =1 |
|
x = 2,5 |
|
|
||
i |
|
|
1/(i!hi) |
Коэффициенты |
(x –x0)(x – x1)…(x – xi) |
Чле- |
||||||
|
|
|
|
|
|
многочлена |
|
|
ны |
|||
0 |
|
|
|
|
a0 |
|
|
|
8,50 |
|
|
8,50 |
1 |
1 |
|
1,00 |
a1= 1 y0 |
|
1 |
|
2,00 |
(x-x0) |
2,50 |
5,00 |
|
|
|
|
|
|
||||||||
|
1!h |
|
||||||||||
|
|
|
|
1!h |
|
|
|
|
||||
2 |
|
1 |
|
|
0,50 |
a2= |
1 |
|
|
|
|
|
-0,25 |
(x-x0)(x- x1) |
3,75 |
- |
||
|
|
2!h2 |
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
0,94 |
||
|
|
|
|
|
|
|
2!h2 |
|
|
|
|
|||||||
3 |
|
1 |
|
|
0,17 |
a3= |
1 |
|
|
|
|
|
0,08 |
(x-x0)(x- x1) (x-x2) |
1,88 |
0,16 |
||
|
|
3!h3 |
|
|
3 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
3!h3 |
|
|
|
|
|
|
|||||
4 |
|
1 |
|
|
|
a4= |
1 |
|
|
|
|
|
|
(x-x0)(x- x1)(x-x2)(x- |
- |
|
||
|
|
|
|
0,04 |
|
|
|
|
|
|
|
-0,04 |
0,04 |
|||||
|
|
4!h4 |
|
4 y |
|
|
|
|
|
|
||||||||
|
|
|
|
|
4 |
|
|
|
x3) |
0,94 |
||||||||
|
|
|
|
|
|
0 |
|
4!h |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
1 |
|
|
|
a5= |
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
5 |
|
|
|
|
|
|
|
(x-x0)(x- x1)(x-x2)(x- |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
5!h5 |
0,01 |
y0 |
|
|
5!h |
5 |
|
|
0,02 |
1,41 |
0,02 |
|||||
|
|
|
|
|
x3)(x-x4) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑= |
12,78 |
Интерполяционный многочлен для рассматриваемого примера будет иметь
вид:
F (x) y |
0 |
|
y0 (x x |
0 |
) 2 y0 (x x |
0 |
)(x x ) |
3 y0 (x x |
0 |
)(x x )(x x |
2 |
) |
|
|
||||||||
|
|
|
h |
|
|
2!h2 |
|
1 |
3!h3 |
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 y0 (x x |
0 |
)(x x )(x x |
2 |
)(x x |
) |
5 y0 (x x |
0 |
)(x x )(x x |
2 |
)(x x |
)(x x |
4 |
). (1.13) |
|||||||||
4!h4 |
|
|
1 |
|
|
3 |
|
5!h5 |
1 |
|
|
3 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставив в него значения коэффициентов a0, a1, .., a5, вычисленные в табл.1.4, получим:
F(x) = P5(x) = 8,5 + 2(x-0) - 0,25(x-0)(x-1) + 0,08(x-0)(x-1)(x-2) – -0,04(x-0)(x-1)(x-2)(x-3)+0,02(x-0)(x-1)(x-2)(x-3)(x-4).
Используя его, вычислим значение f(x) для x = 2,5:
F(2,5) = P5(2,5) = 8,5 + 2(2,5-0) - 0,25(2,5-0)(2,5-1) + 0,08(2,5-0)(2,5-1)(2,5-2) – -0,04(2,5-0)(2,5-1)(2,5-2)(2,5-3)+0,02(2,5-0)(2,5-1)(2,5-2)(2,5-3)(2,5-4) = 12,78.
Таким образом, значение функции y = f(x) для x = 2,5, найденное с помощью интерполяционного многочлена, f(2,5) = 12,78.
Вычисления, представленные в табл. 1.6, удобно выполнять в Excel (рис. 1.2, 1.2-а).
В верхнюю часть таблицы следует ввести исходные данные: значение шага
интерполяции h, который по условию равен 1, значения аргумента x и соответст-
вующие им значения функции f(x) (табл. 1.4), а также значение аргумента x = 2,5, для которого требуется вычислить значение заданной функции, с помощью полученного интерполяционного многочлена.
Реализация вычисления конечных разностей выполняется, как показано в табл. 1.3. Значения конечных разностей и значение f(x0), которые будут использованы в вычислениях по формуле (1.13), выделены в таблице полужирным начертанием. Правильность полученных конечных разностей подтверждают результаты вычислений, выполненные по формуле (1.8) (в ячейках D11 и С12, Е11 и D12
и т.д.).
Коэффициенты интерполяционной формулы (1.13) вычисляют, используя
свойство (1.11): |
1 |
|
1 |
|
1 |
. |
|
(i 1)! h i 1 |
i! h i |
(i 1) h |
|||||
|
|
|
|
Для этого в блоке ячеек В16:В20 реализовано вычисление промежуточных значений коэффициентов таким образом, чтобы каждый последующий элемент
столбца получался из предыдущего, умножением на |
1 |
. Это позволит при не- |
|
i h |
|||
|
|
обходимости легко настраивать полученную таблицу на решение задач любой размерности.
В блоке ячеек D16:D20 вычисляются значения коэффициентов интерполяционного многочлена a0, a1, …, a5 (1.14), путем умножения значений f(x0), и конечных разностей, полученных в блоке С5: H5 на соответствующие им значения промежуточных коэффициентов (В16:В20).
В соответствии с (1.13), каждый коэффициент a1, a2, a3, a4, a5 соответственно требуется умножить на (x –x0), (x –x0)(x- x1), (x –x0)(x- x1)(x-x2),
(x –x0)(x- x1)(x-x2)(x –x3) (x-x4). В блоке ячеек I5: I10 вычисляются значения разностей (x-xi), которые затем используются для вычисления их произведений в блоке Н16:Н20, причем каждый последующий элемент получается из предыдущего. В блоке ячеек I15: I20 выполняется вычисление значений членов интерполяционного многочлена, суммирование которых позволяет получить значение интерполяционного многочлена для x = 2,5.
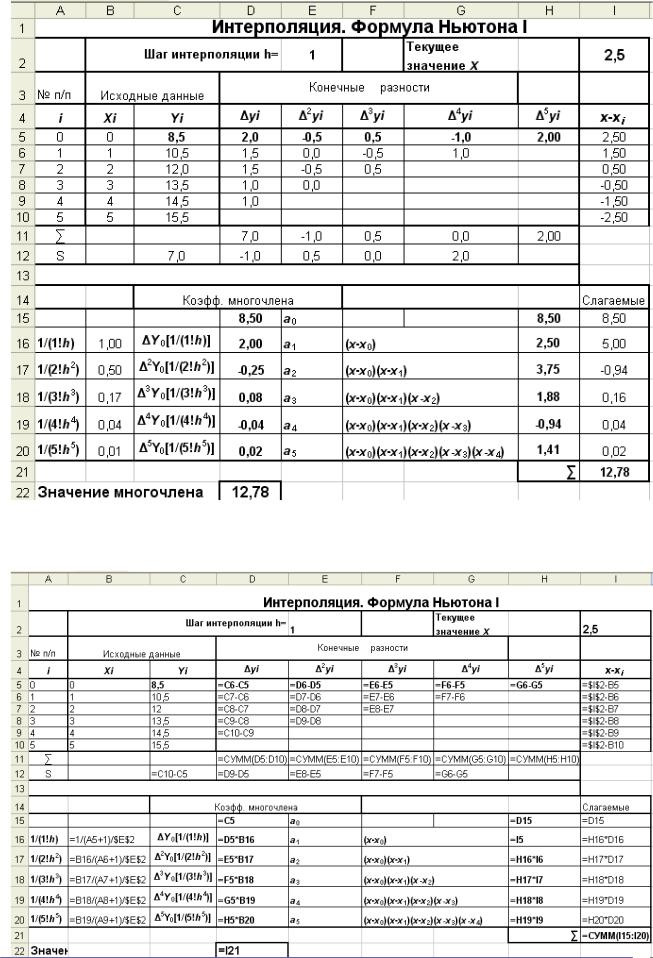
Режим вычислений Рис. 1.2
Режим формул Рис. 1.2-а
Пример 1.2. Функция y = f(x) задана таблицей (табл. 1.7). Построить интерполяционный многочлен, используя первую формулу Ньютона. Найти значение функции для x = 0,6. Решение выполните самостоятельно. При решении используйте формы таблиц.
|
Таблица 1.7 |
|
xi |
yi |
|
0 |
5,4 |
|
1 |
7,3 |
|
2 |
9,4 |
|
3 |
10,5 |
|
4 |
11,8 |
|
5 |
15,9 |
|
Решение. Для функции, заданной табл. 1.7, вычислим конечные разности (форма. 1.1). Для вычисления разностей x-xi в форму введен дополнительный столбец. Вычисление коэффициентов интерполяционного многочлена
F(x) = P5(x) = a0 + a1(x-x0) + a2(x-x0)(x-x1) + a3(x-x0)(x-x1)(x-x2) + + a4(x-x0)(x-x1)(x-x2)(x-x3) + a4(x-x0)(x-x1)(x-x2)(x-x3)(x-x4),
выполним в таблице по форме 1.2.
Форма 1.1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5yi |
x- |
i |
xi |
yi |
yi |
2yi |
3yi |
4yi |
xi |
0 0 5,4
1 1 7,3
2 2 9,4
3 3 10,5
4 4 11,8
5 5 12,9

∑
yn-y0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Форма 1.2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h =1 |
x = 0,6 |
|
|
|
||||||
|
|
|
1/(i!hi) |
Коэффициен- |
(x –x0)(x – x1)…(x – xi) |
|
Чл |
|
||||||||||
|
|
|
|
|
|
ты |
|
|
||||||||||
|
|
|
|
|
многочлена |
|
|
ены |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
a1= |
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
1!h |
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
y0 |
1!h |
|
(x-x0) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
a2= |
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2! |
|
y0 |
|
|
|
|
|
|
|
(x-x0)(x- x1) |
|
|
|
||||
|
|
|
2!h2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
a3= |
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
3! |
|
y0 |
|
|
|
|
|
|
(x-x0)(x- x1) (x-x2) |
|
|
|
|||||
|
|
|
|
3!h3 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
a4= |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
4 y0 |
|
|
|
|
|
|
|
(x-x0)(x- x1)(x-x2)(x-x3) |
|
|
|
|||||
|
|
|
4!h |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
4!h |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
a5= |
|
1 |
|
|
|
|
|
(x-x0)(x- x1)(x-x2)(x-x3)(x- |
|
|
|
||||
|
|
5 y0 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
5!h |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
5 |
|
|
|
|
|
x4) |
|
|
|
|||||
|
|
|
|
|
|
|
5!h |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Искомый интерполяционный многочлен для функции y = f(x) будет иметь вид :
F(x) = P5(x) = + (x-x0) + |
(x-x0)(x-x1) + (x-x0)(x-x1)(x-x2) + |
|
+ (x-x0)(x-x1)(x-x2)(x-x3) + |
(x-x0)(x-x1)(x-x2)(x-x3)(x-x4), |
|
F(0,6) = |
|
|
Значение функции y = f(x) для x = 0,6, найденное с его помощью: |
||
f(0,6) = |
. |
|
1. 4. Вторая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции
Вычисление значений функции для значений аргумента, лежащих в конце таблицы, выполняют, пользуясь второй интерполяционной формулой Ньюто-
на. Интерполяционный многочлен представляют в виде:
F(x) = Pn(x) = a0 + a1(x - xn) + a2(x -xn)(x - xn-1) +
+ a3(x-xn)(x-xn-1)(x-xn-2) + ... + an(x-xn)(x-xn-1)(x-xn-2) …(x-x1), (1.14)
при этом неизвестные значения коэффициентов a0, a1, a2, …, an вычисляют по
формуле |
ai |
|
i yn 1 |
(i = 0, 1, 2, …, n), |
||||||||||
i!h |
i |
|||||||||||||
то есть |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i = 0 a0 = yn, |
|
|
|
|
|
|
|
|
|
|
|
|||
i = 1 |
a1 |
1 yn 1 |
|
= |
|
|
yn 1 |
, |
|
|
||||
|
1 |
|
|
|
h |
|
|
|||||||
|
|
1!h |
|
|
|
|
|
|
|
|
|
|||
i = 2 |
a2 |
2 yn 2 |
|
= |
|
|
2 yn 2 |
и т. д. |
||||||
|
|
|
2 |
|||||||||||
|
|
2!h 2 |
|
|
|
|
|
2!h |
|
|
||||
Обратите внимание на то, что |
|
|
|
|
||||||||||
|
|
|
i 1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
ai 1 |
yn i 1 |
|
|
|
|
. |
|||||||
|
i!hi |
(i 1)h |
||||||||||||
После подстановки найденных коэффициентов ai чают вторую интерполяционную формулу Ньютона:
(1.15)
(1.16)
в выражение (1.14), полу-
Здесь и далее пропущенные места заполните вычисленными коэффициентами или другими параметрами.
F(x) yn yn 1 |
(x |
xn ) |
2 yn 2 |
(x xn )(x xn 1 ) |
3 y0 |
(x xn )(x xn 1 )(x xn 2 ) ... |
|||||
|
|
h |
|
|
|
2!h2 |
|
3!h3 |
|
||
n y0 (x x |
n |
)(x x |
n 1 |
)(x x |
n 2 |
)...(x x ). |
|
(1.17) |
|||
n!hn |
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1.1 (продолжение). Используя вторую интерполяционную формулу Ньютона, построить интерполяционный многочлен для функции, заданной таблицей (табл. 1.4). Найти значение этой функции для x = 4,5.
Решение. Для функции, заданной табл. 1.4, конечные разности были вычислены в табл. 1.5. Для вычисления разностей x-xi в табл. 1.5 был введен дополнительный столбец (табл. 1.5-а). Выделим значения конечных разностей (табл. 1.5- б), которые будут использованы во второй интерполяционной формуле Ньютона (1.15). Вычисление коэффициентов многочлена и его значение для x = 4,5 выполним в таблице (табл. 1.8).
|
|
|
|
|
|
Таблица 1.5-б |
||
|
|
|
yi |
2yi |
3yi |
4yi |
5yi |
x- |
i |
xi |
yi |
xi |
|||||
0 |
0 |
8,5 |
2,0 |
-0,5 |
0,5 |
-1,0 |
2,0 |
4,5 |
1 |
1 |
10,5 |
1,5 |
0,0 |
-0,5 |
1,0 |
|
3,5 |
2 |
2 |
12,0 |
1,5 |
-0,5 |
0,5 |
|
|
2,5 |
3 |
3 |
13,5 |
1,0 |
0,0 |
|
|
|
1,5 |
4 |
4 |
14,5 |
1,0 |
|
|
|
|
0,5 |
|
|
15,5 |
|
|
|
|
|
- |
5 |
5 |
|
|
|
|
|
0,5 |
|
|
∑ |
|
7,0 |
-1,0 |
0,5 |
0,0 |
2,0 |
|
|
yn-y0 |
7,0 |
-1,0 |
0,5 |
0,0 |
2,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.8 |
|
|
|
|
|
|
h =1 |
|
|
|
|
|
|
|
x = 4,5 |
|
|
||
|
|
|
1/(i!hi) |
Коэффициенты |
(x –x5)(x – x4)…(x – x0) |
|
Чле- |
||||||||||
|
|
|
|
|
|
|
многочлена |
|
|
ны |
|||||||
|
|
|
|
|
|
|
a0 |
|
|
|
|
|
|
15,5 |
|
|
15,5 |
|
|
1 |
|
|
|
|
a1= 1 yn 1 |
1 |
|
|
|
- |
|
||||
|
|
|
|
1,00 |
1!h |
1,0 |
(x-x5) |
-0,50 |
|||||||||
|
1!h |
|
|||||||||||||||
|
|
|
|
|
0,5 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0,50 |
a2= |
|
1 |
|
|
|
|
0,0 |
(x-x5)(x- x4) |
- |
0,00 |
|
|
|
2!h2 |
|
2 yn 2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
0,25 |
||||||||||
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2!h |
|
|
|
|
||||
|
|
1 |
|
|
|
|
a3= |
|
1 |
|
|
|
|
|
|
- |
|
|
|
|
|
0,17 |
3 yn 3 |
|
|
|
|
|
0,08 |
(x-x5)(x- x4) (x-x3) |
-0,03 |
||||
|
|
3!h3 |
|
|
|
|
|
0,38 |
|||||||||
|
|
|
|
3!h3 |
|
|
|
||||||||||
|
|
1 |
|
|
0,04 |
a4= |
|
1 |
|
|
|
0,04 |
(x-x5)(x- x4)(x-x3)(x-x2) |
- |
-0,04 |
|
|
4!h4 |
|
4 yn 4 |
|
|
|
|
|||||||
|
|
|
|
|
|
0,94 |
|||||||||
|
|
4!h |
4 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
a5= |
|
1 |
|
|
|
|
|
- |
|
|
|
|
|
0,01 |
5 yn 5 |
|
|
|
|
0,02 |
(x-x5)(x-x4)(x-x3)(x-x2)(x-x1) |
-0,05 |
|||
|
|
5!h5 |
|
|
|
|
3,28 |
||||||||
|
|
|
|
5!h5 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑= |
14,88 |
Интерполяционный многочлен (1.15) будет иметь вид:
F(x) = P5(x) = 15,5 + 1·(x-5) + 0·(x-5)(x-4) + 0,08· (x-5)(x-4)(x-3) + + 0,04·(x-5)(x-4)(x-3)(x-2) + 0,02·(x-5)(x-4)(x-3)(x-2)(x-1)
F(4,5) = P5(4,5) = 15,5 + 1·(4,5-5) + 0·(4,5-5)(4,5-4) + 0,08· (4,5-5)( 4,5-4)(4,5-3) + + 0,04·(4,5-5)(4,5-4)(4,5-3)(4,5-2) + 0,02·(4,5-5)(4,5-4)(4,5-3)(4,5-2)(4,5-1) = 14,88
Значение функции y = f(x) для x = 4,5, найденное с помощью интерполяционного многочлена, f(4,5) = 14,88.
Вычисления, представленные в табл. 1.8, выполнены в Excel и показаны на рис. 1.3, 1.3 - a.
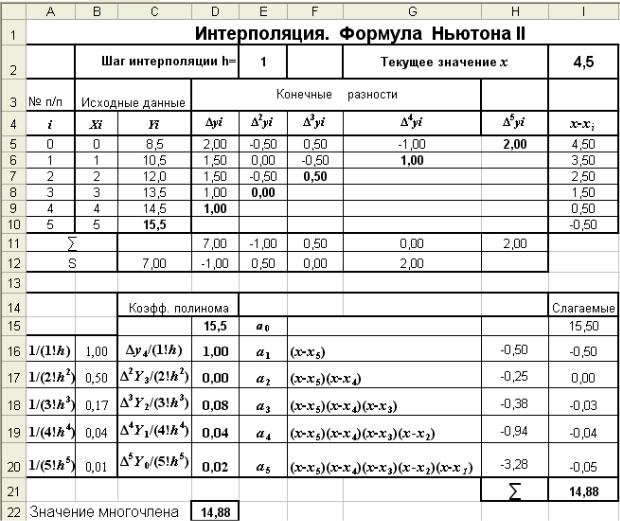
Режим решения Рис. 1.3
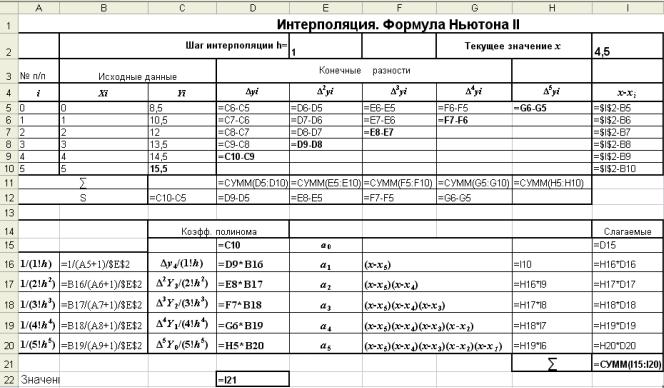
Режим формул Рис. 1.3 – а
Пример 1.2 (продолжение). Используя вторую интерполяционную формулу Ньютона, построить интерполяционный многочлен для функции, заданной таблицей (табл. 1.7). Найти значение этой функции для x = 6.
Решение. Для функции, заданной табл. 1.7, вычислим конечные разности, которые будут использованы во второй интерполяционной формуле Ньютона в таблице по форме 1.3. Для вычисления разностей x-xi в таблицу введем дополнительный столбец. Вычисление коэффициентов многочлена и его значение для x = 6 выполним в таблице по форме 1.4.
Форма 1.3
|
|
|
|
2yi |
3yi |
4yi |
5yi |
x- |
i |
xi |
yi |
yi |
xi |
||||
0 |
0 |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
5 |
5 |
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
yn-y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Форма 1.4 |
|
|
|
|
|
|
|
h =1 |
|
|
|
|
|
|
|
|
x = 6 |
|
|
|
|
|
1/(i!hi) |
Коэффициенты |
|
(x –x5)(x – x4)…(x – xi) |
|
Чле- |
|||||||||||
|
|
|
|
|
|
|
многочлена |
|
|
|
ны |
|||||||
|
|
|
|
|
|
|
a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1,00 |
a1= |
|
1 |
|
|
|
|
(x-x5) |
|
|
||
|
1!h |
|
|
|
|
|
|
|
|
|||||||||
|
1 yn 1 |
|
|
|
|
|
|
|
||||||||||
|
|
1!h |
|
|
|
|
|
|||||||||||
|
1 |
|
|
|
0,50 |
a2= |
|
|
1 |
|
|
|
|
(x-x5)(x- x4) |
|
|
||
|
|
2!h2 |
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
yn 2 |
|
|
2!h2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
0,17 |
a3= |
|
|
1 |
|
|
|
|
(x-x5)(x- x4) (x-x3) |
|
|
||
|
|
3!h3 |
|
|
3 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
yn 3 |
|
|
3!h3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
0,04 |
a4= |
|
1 |
|
|
|
|
(x-x5)(x- x4)(x-x3)(x-x2) |
|
|
|||
|
|
4!h4 |
4 |
|
|
|
|
|
|
|
||||||||
|
|
yn 4 |
|
4!h4 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
0,01 |
a5= |
|
1 |
|
|
|
|
(x-x5)(x- x4)(x-x3)(x-x2)(x-x1) |
|
|
|||
|
|
5!h5 |
|
5 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
yn 5 |
|
|
5!h5 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑= |
|
F(x) = P5(x) = a0 + a1(x-x5) + a2(x-x5)(x-x4) + a3(x-x5)(x-x4)(x-x3) + + a4(x-x5)(x-x4)(x-x3)(x-x2) + a4(x-x5)(x-x4)(x-x3)(x-x2)(x-x1)
F(x) = P5(x) = |
+ ·(x-x5) |
·(x-x5)(x-x4) |
· (x-x5)(x-x4)(x- |
x3) + |
|
|
|
·(x-x5)(x-x4)(x-x3)(x-x2) ·(x-x5)(x-x4)(x-x3)(x-x2)(x-x1)
F(6) = P5(6) =
Значение функции y = f(x) для x = 6, найденное с помощью интерполяционного многочлена (1.9), F(6) = .
1.5. Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Лагранжа является наиболее общей формулой интерполирования. Он пригоден для интерполирования функций, как с постоянным, так и с переменным шагом. Другими словами, интерполяционный многочлен Лагранжа может использоваться для интерполирования функций как с равноотстоящими, так и с не равноотстоящими узлами интерполяции. Интерполяционный многочлен Лагранжа строится в виде:
Pn(x) = a0(x-x1)(x-x2)…(x-xn) + a1(x- x0)(x-x2)…(x-xn) + …
+ak(x- x0)(x-x1)…(x-xk-1) (x-xk+1) …(x- xn) + … + an(x- x0)(x-x1)…(x-xn-1). (1.18)
Определим коэффициенты многочлена (1.18).
Пусть x = x0, тогда
|
a0 |
|
|
y0 |
|
|
, |
||
|
(x0 x1 )(x0 x2 )...(x0 |
xn ) |
|||||||
|
|
|
|
|
|||||
x = x1, |
a1 |
|
|
y1 |
|
|
, |
|
|
|
(x1 x0 )(x1 x2 )...(x1 xn ) |
|
|||||||
|
|
|
|
|
|||||
|
|
|
|
…………………… |
|
|
|
||
x = xn, |
an |
|
|
yn |
|
|
|
||
(xn x0 )(xn |
x1 )...( xn xn 1 ) |
||||||||
|
|
|
|
||||||
и интерполяционная формула Лагранжа будет иметь вид:
n |
(x x0 )(x x1 )...(x xk 1 )(x xk 1 )(x xn ) |
|
|
|
Pn (xk ) |
|
yk . |
(1.19) |
|
(xk x0 )(xk x1 )...(xk xk 1 )(xk xk 1 )...(xk xn ) |
||||
k 0 |
|
|
Если функция задана в двух узлах, интерполяция будет осуществляться интерполяционным многочленом Лагранжа первой степени:
|
|
|
|
P1(x) = a0(x-x1) + a1(x-x0). |
|
|
|
(1.20) |
|||||||||||
При x = x0 |
a0 |
|
|
y0 |
|
, |
x = x1 |
a1 |
|
|
y1 |
|
, |
|
|||||
|
|
|
|
(x1 x0 ) |
|
||||||||||||||
(x0 |
x1 ) |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
P1(x) = |
|
(x x1 ) |
y0 |
|
(x x0 ) |
|
y1 . |
|||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
(x |
0 |
x ) |
|
|
(x x |
) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
0 |
|
|
|
|
Пример 1.3. Функция f(x) задана таблицей (табл. 1.9):
Таблица 1.9
x |
y |
1 |
4 |
5 |
12 |
Построить интерполяционный многочлен Лагранжа и с его помощью вычислить значения функции для значений аргумента x, равных 2, 3, 4.
Решение. Из условия известно, что x0 = 1, x1 = 5. Найдем коэффициенты многочлена a0 и a1.
a |
0 |
|
y0 |
|
4 |
1, |
a |
|
y1 |
|
12 |
3. |
|
|
|
|
|
||||||||||
|
|
|
|
||||||||||
|
|
(x0 |
x1 ) |
1 5 |
|
1 |
(x1 |
x0 ) |
|
5 1 |
|||
|
|
|
|
|
|
||||||||
Используя формулу (1.3), получим интерполяционный многочлен
P1(x) =-1(x-5) + 3(x-1).
Вычислим значения функции для x = 2, 3, 4:
P1(2) = -1(2-5) + 3(2-1) = 6.
P1(3) = -1(3-5) + 3(3-1) = 8.
P1(4) = -1(4-5) + 3(4-1) = 10.
В результате получим (табл. 1.10):
|
|
|
|
Таблица 1.10 |
|
|
|
|
|
|
|
x |
1 |
2 |
3 |
4 |
5 |
y |
4 |
6 |
8 |
10 |
12 |
Вычисления удобно производить в Excel (рис. 1.4, 1.4 – а).

Режим решения Рис. 1.4
Режим формул Рис. 1.4 – а
Если функция задана в трех узлах, интерполяция будет осуществляться интерполяционным многочленом Лагранжа второй степени:
|
P2(x) = a0(x-x1)(x-x2) |
+ a1(x-x0)(x-x2) + a2(x-x0)(x-x1). |
(1.21) |
|||||||||
При x = x0 |
a0 |
|
|
y0 |
|
, |
|
x = x1 a1 |
|
y1 |
, |
|
|
|
|
|
(x1 x0 )(x1 x2 ) |
||||||||
(x0 |
x1 )(x0 x2 ) |
|
||||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x = x2 |
a2 |
|
|
y2 |
|
, |
|
|
|
|
|
|
(x2 |
x0 )(x2 |
x1 ) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
P2(x) = |
(x x1 )(x |
x2 ) |
|
y0 |
|
(x x0 )(x x2 ) |
y1 |
|
(x x0 )(x |
x1 ) |
y2 . |
(1.22) |
||||||||||||||||
(x |
0 |
x )(x |
0 |
x |
2 |
) |
(x |
x |
0 |
)(x |
x |
2 |
) |
(x |
2 |
x |
0 |
)(x |
2 |
x ) |
||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|||||||||
Пример 1.4. Функция f(x) задана таблицей (табл. 1.11).
Таблица 1.11
x |
y |
1 |
4 |
5 |
12 |
7 |
30 |
Построить интерполяционный многочлен Лагранжа и с его помощью вычислить значения функции для аргумента x, принимающего значения 2, 3, 4, 6.
Решение. Найдем коэффициенты интерполяционного многочлена Лагранжа a0, a1, a2.
a0 |
|
|
|
|
y0 |
|
|
|
|
|
|
4 |
|
|
1 |
0,17; |
|||||
|
(x0 |
x1 )(x0 |
x2 ) |
(1 5)(1 7) |
6 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
a1 |
|
|
|
y1 |
|
|
|
|
|
12 |
|
|
|
|
3 |
1,5; |
|||||
(x1 |
x0 )(x1 |
x2 ) |
(5 1)(5 7) |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
a2 |
|
|
|
y2 |
|
|
|
|
|
|
30 |
|
|
|
|
|
5 |
2,5. |
|||
|
(x2 x0 )(x2 x1 ) |
(7 |
1)(7 5) |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
Получим интерполяционный многочлен: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
P2(x) = 1 |
(x 5)(x 7) |
3 (x 1)(x 7) |
5 |
(x 1)(x 5). |
|||||||||||||||||
6 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
Используя его, вычислим значение функции для x = 2, 3, 4, 6.
P2(2) = |
1 |
(2 5)(2 7) |
3 |
|
(2 1)(2 7) |
|
5 |
(2 1)(2 5) |
2,5; |
|
|
6 |
|
2 |
|
|
|
2 |
|
|
|
P2(3) = |
1 |
(3 5)(3 7) |
3 |
(3 1)(3 7) 5 |
(3 1)(3 5) 3,3; |
|||||
|
6 |
|
2 |
|
|
2 |
|
|
|
|
P2(4) = |
1 |
(4 5)(4 7) |
3 |
(4 1)(4 7) |
|
|
5 |
(4 1)(4 5) |
6,5; |
|
|
6 |
|
2 |
|
|
|
2 |
|
|
|
P2(6) = 16 (6 5)(6 7) 32 (6 1)(6 7) 52 (6 1)(6 5).
В результате получим (табл. 1.12) |
|
|
|
|
||||
|
|
|
|
|
|
|
Таблица 1.12 |
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
y |
4 |
2,5 |
3,3 |
6,5 |
12 |
20 |
30 |
Вычисления удобно выполнять в Excel (рис. 1.5, 1.5 - а).
Режим решения Рис. 1.5
Режим формул Рис. 1.5 - а
Обратите внимание: значения функции в рассматриваемых примерах совпадают в общих узлах интерполяции; степень многочлена (наличие еще одного узла во втором примере) весьма существенно влияет на значение функции между узлами интерполяции (табл. 1.10, 1.12); появление еще одного узла интерполяции заставляет снова выполнять вычисления всех коэффициентов.
Преимущество формул Ньютона по сравнению с формулой Лагранжа состоит в том, что добавление новых узлов интерполяции не приведет к проведению расчетов заново.
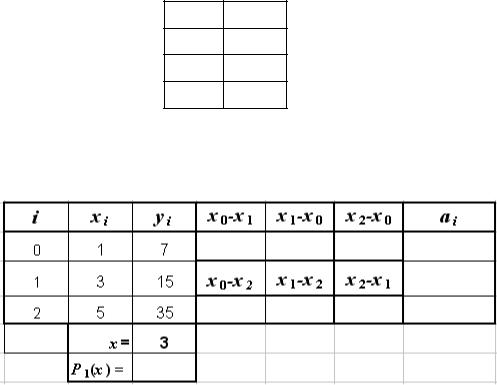
Пример 1.5. Для функции, заданной таблицей, построить интерполяционный многочлен Лагранжа и с его помощью вычислить значение функции для x = 2.
Таблица 1.13
x |
y |
1 |
7 |
3 |
15 |
5 |
35 |
Решение выполните самостоятельно. Для удобства решения используйте таблицу по форме 1.5.
Форма 1.5
