Числовые характеристики случайных величин

1 . Математическое ожидание (среднее значение)

Определение: Математическим ожиданием называется - для дискретной случайной величины:

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)

- для непрерывной случайной величины:;

Интеграл должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)

Свойства математического ожидания:

a .   Если С - постоянная величина, то МС = С b .   МСх = СМх c .   Математическое ожидание суммы случайных величин всегда равно сумме их математических ожиданий: М(х+y) = Мх + Мy d .   Вводится понятие условного математического ожидания. Если случайная величина принимает свои значения х_i с различными вероятностями p(x_i/H_j) при разных условиях H_j, то условное математическое ожидание определяется

как или;

Если известны вероятности событий H_j, может быть найдено полное

математическое ожидание: ;

.

e .   Если f(x) - есть функция случайной величины х, то определено понятие математического ожидания функции случайной величины:

- для дискретной случайной величины: ;

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся.

-для непрерывной случайной величины:;    )

Интеграл должен быть абсолютно сходящимся.

2 .   Дисперсия случайной величины Определение: Дисперсией случайной величины х называется математическое ожидание квадрата отклонения значения величины от ее математического ожидания:   Dx = M(x-Mx)²

- для дискретной случайной величины: ;

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)

- для непрерывной случайной величины: ;

Интеграл должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)

Свойства дисперсии: a .   Если С - постоянная величина, то DС = 0 b .   DСх = С²Dх c .   Дисперсия суммы случайных величин всегда равно сумме их дисперсий только, если эти величины независимы (определение независимых величин) d .   Для вычисления дисперсии удобно использовать формулу:

  Dx = Mx² - (Mx)²      

Связь числовых характеристик и параметров типичных распределений

распределение	параметры	формула	Mx	Dx
равномерное	a , b		(b+a) / 2	(b-a)2 / 12
нормальное	a , σ		a	σ2
Бернулли	n , p		np	npq
Пуассона	a		a	a

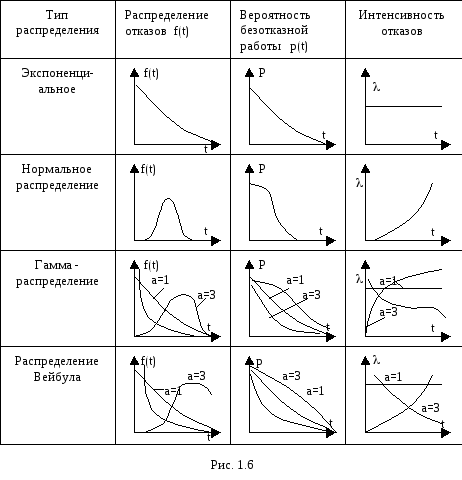
Приложение б Законы распределения отказов

Возможны два пути вычисления показателей надежности х объектов по данным об отказах:

1. определение экспериментального распределения наработки до отказа;

2. вычисление параметров теоретического распределения наработки до отказа.

В качестве теоретических распределений наработки до отказа могут быть использованы любые применяемые в теории вероятностей непрерывные распределения.

Из теории надежности известно, что случайное время наступления отказов может быть описано математическими законами распределения случайных величин, что как раз и делает науку о надежности строгой.

В основе инженерных методов расчета надежности, учитывающих внезапные отказы, положен экспоненциальный закон распределения, в методиках расчета, учитывающих влияние параметрических отказов (есть ли определение параметрических отказов отказах*) – нормальный закон.

В пользу применения простейших законов распределения можно привести ряд соображений. Во-первых, для целого ряда компонентов и систем эти законы находят статистическое подтверждение. Кроме того, многие виды распределения с ростом числа компонентов или увеличением времени испытаний аппаратуры асимптотически стремятся к простейшим законам. Наконец, вероятностные показатели чаще всего используются для сравнительной оценки надежности проектируемых систем, и привлечение простых моделей к инженерным расчетам наиболее оправданно. Если принять, что структурная надежность объектов в основном определяется катастрофическими отказами, то естественно предположить, что интенсивность отказов будет падать, за счет устранения дефектных элементов и мест некачественной сборки. Параметрические отказы характеризуют надежность конструктивно-эксплуатационных показателей объектов, что обуславливает рост интенсивности параметрических отказов под влиянием внешних условий и внутренних дестабилизирующих факторов, например износа деталей.

Примем, что отказы обеих групп не зависят между собой. Тогда общая надежность объекта будет равна p(t)=p_n*p_nn, а суммарная интенсивность отказов очень близка к картине развития отказов в реально функционирующей системе электроснабжения.

Именно поэтому при исследовании надежности самых разнообразных объектов обращаются к небольшому кругу известных распределений.

1.Распределение Пуассона. Характеризует появление редких событий.

Например, вероятность для случайных событий, образующий простейший поток, распределены по закону Пуассона

при n >0

где Рn(t) - вероятность возникновения в течение времени t ровно n событий (отказов);  - параметр распределения, совпадающий с параметром потока событий. Если в выражении принять n = 0, то получим - вероятность безотказной работы объекта за время t при интенсивности отказов  = const. Нетрудно доказать, что если восстанавливаемый объект при отсутствии восстановления имеет характеристику  = const, то, придавая объекту восстанавливаемость, мы обязаны записать (t) = const;  =  Это свойство широко используется в расчетах надежности ремонтируемых устройств