Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северо-Западный государственный заочный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1_kolebaniya-i-volnyi--umknovoe1.pdf

Скачиваний:

Добавлен:

16.02.2016

Размер:

2.06 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

Раздел 2. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ПЕРЕМЕННЫЙ ТОК

Вразделе 2 изучаются две темы: 2.1. Электрический колебательный

контур; 2.2. Переменный электрический ток.

Вконце каждой темы вы должны ответить на поставленные вопросы, а по завершению изучения раздела выполняется тестовое задание.

Максимально возможное число баллов, которое можно получить при работе с материалом данного раздела, равно 20.

Подробное изложение материала раздела представлено в учебном пособии А.Б. Федорцова, В.М. Цаплева «Курс физики. Колебания и волны. Волно-

вая оптика», а также: [1], c. 261…263, 276…283; [2], c.302…303, 314…317.

По материалам раздела выполняются задачи 421…435 из контрольной работы № 4.

Электромагнитные колебания возникают при колебательном движении заряженных тел. Возникающие при этом токи меняются с течением времени. Законы Ома, Джоуля-Ленца и правила Кирхгоффа были установлены для постоянного тока. Однако они остаются справедливыми и для мгновенных значений изменяющихся тока и напряжения, если их изменения не происходят

слишком быстро. Если характерное время τ = сl , где l – длина электрической

цепи, а с = 3 108 м/с – скорость света в вакууме, много меньше периода колеба-

ния тока (τ << Т), то такие токи называются квазистационарными. Для таких токов справедливы все законы постоянного тока. Ток промышленной частоты

(ν = 50 Гц), например, стационарен для цепей длиной до 100 км. В дальнейшем будем полагать, что рассматриваемые токи квазистационарны.

2.1.Электрический колебательный контур

2.1.1.Свободные незатухающие электромагнитные колебания

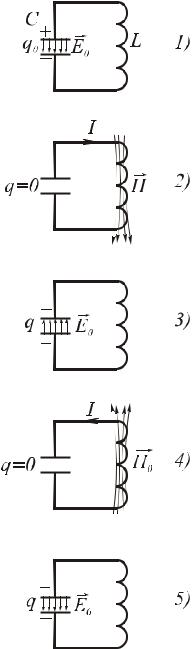
В цепи, содержащей индуктивность и емкость (рис. 2.1), могут возникать электромагнитные колебания. Поэтому такая цепь называется колебатель-

ным контуром.

Рассмотрим идеальный случай, когда полное сопротивление такого контура равно 0. Сообщим конденсатору заряд: +q на одной обкладке и –q – на другой (рис. 2.1 – 1). Между обкладками конденсатора возникнет электрическое поле, энергия кото-

рого W =	1 q2	. Конденсатор начнет разряжаться
e	2 C
	2 C

через индуктивность, т.е. в контуре потечет ток. В результате энергия электрического поля будет уменьшаться, но зато возникнет всё возрастающая энергия магнитного поля, обусловленного током,

текущим через индуктивность	W =	1	LI 2	. По-

	m	2

скольку активное сопротивление контура равно нулю, полная энергия W =We +Wm не расходуется на нагревание проводов и остается постоянной. Поэтому в момент, когда напряжение на конденсаторе, его заряд и энергия электрического поля обращает-

Рис. 2.1

ся в ноль, энергия магнитного поля и ток достигают максимального значения (рис. 2.1 – 2). Начиная с этого момента, ток течет за счет ЭДС самоиндукции. В дальнейшем ток уменьшается и, наконец, становится равным 0, когда конденсатор перезаряжается в обратном направлении: -q и +q (рис. 2.1 – 3). Затем те же процессы протекают в обратном направлении (рис. 2.1, 4), после чего система приходит в исходное состояние (рис. 2.1, 5) и весь

цикл повторяется многократно. В ходе этого процесса периодически изменяются (т.е. колеблются) заряд на обкладках, напряжение на конденсаторе и сила тока в контуре. Колебания сопровождаются взаимным превращением энергии электрического и магнитного полей.

Проведем количественную оценку протекающих процессов, при этом будем считать положительным ток, заряжающий конденсатор.

(2.1)

I = dt = q .

Закон Ома для участка цепи между обкладками конденсатора 1 и 2 имеет

вид

IR = ϕ1 − ϕ2 + ε12 .

(2.2)

В данном случае R = 0, ϕ − ϕ

= −

и ε

= −L dI

, тогда

0 = −

− L dI .

(2.3)

d(q)

Учитывая, что dt =

= q , получим

+ LC q = 0 .

(2.4)

Таким образом, в данном колебательном контуре происходят электромаг-

нитные гармонические колебания с частотой

ω0 =

(2.5)

называемой собственной частотой контура. Для периода колебаний из (2.5) получается так называемая формула Томсона

Т = 2π LC .	(2.6)
Решением (2.4) является
q = qm cos(ω0t + α).	(2.7)

Напряжение на конденсаторе отличается от заряда множителем С1 :

U =

cos(ω0t + α)

=Um cos(ω0t + α).

(2.8)

Продифференцировав функцию (2.7) по времени, получим выражение

для силы тока:

I = −ω

sin(ω

t + α)= I

ω t

+ α +

(2.9)

cos

Сила тока опережает по фазе напряжение на конденсаторе на

π .

Из формул (2.8) и (2.9) следует, что U

и I

= ω q

. Отсюда

получается соотношение для амплитуд тока и напряжения:

		Um =	L	Im .	(2.10)
		Um =		Im .	(2.10)
			C
Величина ρ =	L	называется волновым сопротивлением.
Величина ρ =	C	называется волновым сопротивлением.
	C

2.1.2. Затухающие электромагнитные колебания

Всякий реальный контур обладает активным со-

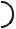противлением. Энергия, запасенная в контуре, посте-

пенно расходуется на этом сопротивлении на нагрева-

ние, вследствие чего свободные колебания затухают. Рис. 2.2 Рассмотрим контур, содержащий сопротивление (рис.

2.2). Закон Ома для такого контура имеет вид:

IR = −	q	− L	dI	.	(2.11)
	C
			dt

Разделив это уравнение на L и, обозначив I = q&, а dIdt = q&&, получим

q&&+	R	q&	+	1	q = 0 .	(2.12)
				LC
	L

Обозначив β = 2RL и учтя, что ω02 = LC1 , получаем

(2.13)

+ 2βq

+ ω0q = 0 .

Это есть уравнение затухающих гармонических колебаний.

При слабом затухании (β2 << ω02), т.е.

, колебания заряда на

конденсаторе будут происходить по закону

q = qm0e−βt cos(ωt +t),

(2.14)

где

qm0 –

амплитуда

заряда

в начальный

момент времени, а

ω =

ω02 −β2 =

−

. Таким образом,

частота затухающих колебаний

4L2

меньше собственной частоты ω0, правда для слабого затухания эта разность незначительна.

Разделив (2.14) на емкость С, получим закон колебания напряжения на конденсаторе:

U =			1		qm0 e−βt cos(ωt + α)=Um0 e−βt cos(ωt + α).				(2.15)
U =					qm0 e−βt cos(ωt + α)=Um0 e−βt cos(ωt + α).				(2.15)
			C
Чтобы найти силу тока в цепи, надо продифференцировать (2.14) по вре-
мени. После преобразований данная зависимость будет иметь вид:
					I = ω q		m0	e−βt cos(ωt + α + Ψ),	(2.16)
			0				m0
где cos Ψ = −	β			, а sin Ψ = −			ω	. Поскольку cos Ψ < 0, а sin os Ψ > 0, значение
где cos Ψ = −				, а sin Ψ = −		ω		. Поскольку cos Ψ < 0, а sin os Ψ > 0, значение
	ω	0				ω
		0					0
Ψ заключено в пределах от π							до π. Это означает, что, при наличии в контуре
			2

активного сопротивления, сила тока опережает по фазе напряжение на конден-

саторе более, чем на π2 .

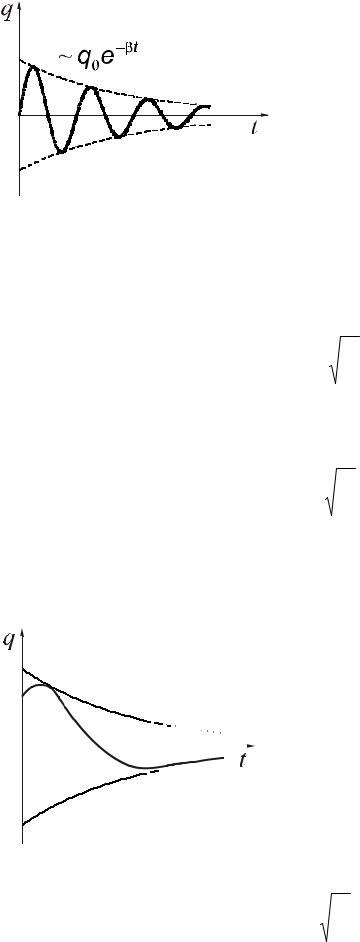
Зависимость заряда на конденсаторе от времени изображена на рис. 2.3. Зависимости от времени напряжения и силы тока имеют аналогичный вид. Для колебательного контура логарифмический декремент имеет вид:

Рис. 2.3

λ = βT =	R	2π	=	πR	.	(2.17)
	2L	ω
				Lω

Для слабого затухания (β2 << ω02) ω ≈ ω0 и

λ = πR	C	.	(2.18)

	L

Добротность колебательного контура, с учетом ее связи с логарифмиче-

ским декрементом (Q = π/λ), равна

Q =	1	L	=	ρ	,	(2.19)
	R	C		R

т.е. добротность контура равна отношению волнового сопротивления ρ к его активному сопротивлению R. Чем выше добротность контура, тем медленнее будут затухать колебания.

При большом затухании (β2 ≥ ω02), т.е.

≥

, вместо колебаний происходит

апериодический разряд конденсатора (рис.

2.4). Сопротивление контура, при котором

колебательный процесс переходит в апе-

риодический, называется критическим, а

Рис. 2.4

его значение равно

R = 2

= 2ρ.

(2.20)

k	C
	C
	44

2.1.3. Вынужденные электромагнитные колебания

Вынужденные электромагнитные колебания в контуре осуществляются, если включить последовательно с элементами контура переменную ЭДС или, разорвав контур, подать на образовавшиеся контакты переменное напряжение

(рис. 2.5):

		Рис. 2.5
U =Um cos ωt .							(2.21)
В результате закон Ома имеет вид:
IR = −	q	− L	dI	+Um cos ωt .			(2.22)
	C
			dt
Это выражение преобразуется к виду:
q&&+ 2βq& + ω02q =					Um	cos ωt .	(2.23)

					L

Уравнение (2.23) является дифференциальным уравнением вынужден-

ных колебаний. Решение данного уравнения для установившихся колебаний заряда имеет вид:

q = qm cos(ωt − Ψ),

(2.24)

где амплитуда колебаний заряда равна

qm =			Um			,	(2.25)

		R2		ωL −	1 2
	ω		+

					ωC

а сдвиг фаз

tgΨ =			R			.			(2.26)
tgΨ =		1		−ωL					(2.26)
	ωC			−ωL
	ωC
Продифференцировав выражение (2.24) по времени, найдем силу тока в
контуре при установившихся колебаниях:
I = Im cos(ωt −ϕ),									(2.27)
где Im = ωqm и
		π			ωL −		1
		π			ωL −		ωC
tgϕ = tg Ψ −				=			ωC	.	(2.28)
tgϕ = tg Ψ −				=		R		.	(2.28)
		2				R

Отсюда следует, что ток отстает по фазе от напряжения (ϕ > 0) в случае

ωL > 1/ωC, и опережает напряжение (ϕ < 0) в случае ωL < 1/ωC. Амплитуда силы тока определяется выражением:

Im =			Um			.	(2.29)

	R2		ωL		1 2
		+		−

					ωC
Если учесть, что напряжение на активном сопротивлении UR = IR, напря-

жение на конденсаторе UC = q/C, а напряжение на индуктивности U L = L		dI	,

		dt
получим из (2.22):
UR +UC +UL =Um cos ωt .	(2.30)
Таким образом, сумма напряжений на отдельных элементах контура рав-

на в каждый момент времени напряжению, приложенному извне. Напряжения на отдельных элементах контура меняются со временем по следующим законам:

	UR = RI = RIm cos(ωt −ϕ),							(2.31)
	q		q	m			π
UC =		=		m	cos(ωt − Ψ)=UCm cos	ωt −ϕ−	,	(2.32)
UC =	C	=			cos(ωt − Ψ)=UCm cos	ωt −ϕ−	,	(2.32)
	C		C				2

где	Ucm =	qm	=	Im	.	(2.33)

		C		ωC

	dI			π
UL = L		=ULm cos	ωt −ϕ+	,	(2.34)
UL = L	dt	=ULm cos	ωt −ϕ+	,	(2.34)
	dt			2
где		ULm = ωLIm .			(2.35)

Сопоставление формул (2.27), (2.31), (2.32) и (2.34) показывает, что на-

пряжение на конденсаторе отстает по фазе от силы тока на π2 , а напряжение на

индуктивности опережает ток на π2 . Напряжение на активном сопротивлении

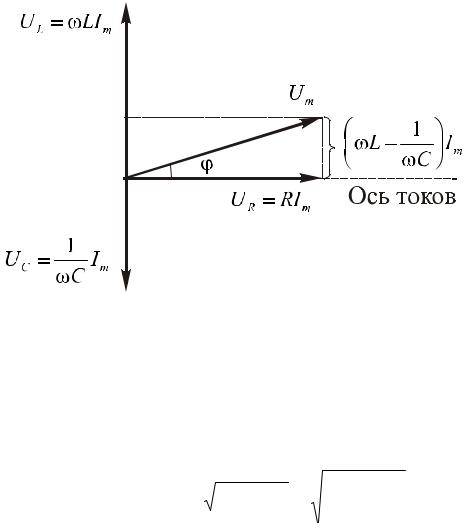
меняется в одной фазе с током. Фазовые соотношения можно представить с помощью векторной диаграммы (рис. 2.6). Согласно (2.30) сумма векторов UR, UL и UC должна быть равна вектору Um.

Рис. 2.6

При приближении частоты ω к частоте собственных колебаний контура начинают проявляться резонансные явления. Резонансная частота для колебаний заряда q и напряжения на конденсаторе UC равна

ω	q рез	= ω	= ω2	− 2β2	=	1	−	R2	.	(2.36)

		U рез	0			LC		2L2

При малом затухании она практически равна ω0. Отношение амплитуды напряжения на конденсаторе при резонансе UC m рез к амплитуде внешнего напряжения Um будет равно

UCm рез

= Q.

(2.37)

ω CR

Амплитуда силы тока имеет максимальное значение при ωL −

= 0.

ωC

Следовательно, резонансная частота для силы тока

ω	I рез	= ω =	1	.	(2.38)

		0	LC

Рис. 2.7

Рис. 2.8

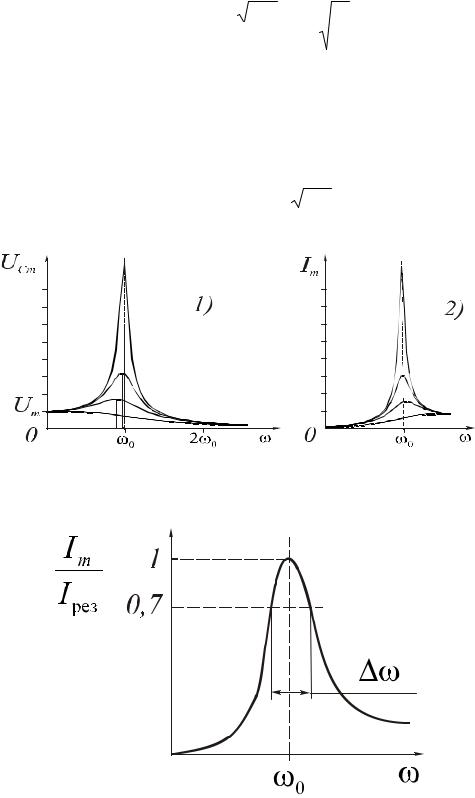
Резонансные кривые напряжения на конденсаторе и силы тока показаны на рис. 2.7. Добротность контура Q определяет также остроту резонансных кривых:

Q =	ω0	,	(2.39)
	ω

где Δω – ширина пика по уровню 0,7 (рис. 2.8).

Вопросы для самопроверки

1.От чего зависит период собственных колебаний в колебательном контуре?

2.Чем определяется добротность колебательного контура?

3.От чего зависит сдвиг фаз между током и напряжением в колебательном контуре?

4.Что такое резонанс в колебательном контуре? Запишите выражение для резонансной частоты.

5.Нарисуйте и проанализируйте резонансные кривые для тока и напряжения.

2.2. Переменный электрический ток

Установившиеся вынужденные электромагнитные колебания можно рассматривать как протекание в цепи, обладающей емкостью, индуктивностью и активным сопротивлением, переменного тока под действием переменного напряжения:

U =Um cos ωt .							(2.40)
Ток в цепи равен
I = Im cos(ωt −ϕ).							(2.41)
Амплитуда тока определяется амплитудой напряжения Um, параметрами
цепи С, L, R и частотой ω:
Im =		Um				.	(2.42)
				1
	R2				2
		+ ωL	−

				ωC

Разность фаз ϕ между током и напряжением также зависит от параметров цепи и частоты

	ωL −	1
tgϕ =		ωC	.	(2.43)

	R

2.2.1. Импеданс цепи

Полным электрическим сопротивлением или импедансом называется величина

			Z = R2		1 2
				+ ωL −		.	(2.44)
				+ ωL −		.	(2.44)
					ωC
	Величина ХL = ωL называется			индуктивным			сопротивлением, а
ХС =	1		- емкостным сопротивлением. Х = ХL – XC носит название реак-
ХС =		ωС
		ωС

тивного сопротивления.

Если активное сопротивление цепи R равно 0, т.е. цепь обладает только реактивным сопротивлением, то протекание тока в такой цепи не приводит к выделению теплоты Джоуля-Ленца.

2.2.2. Мощность в цепи переменного тока

Мгновенное значение мощности равно произведению мгновенных значений напряжения и силы тока:

P(t)=U (t) I (t)=Um cos ωt Im cos(ωt −ϕ).					(2.45)
Это выражение можно преобразовать к виду:
P(t)=	1	Um cos ϕ +	1	Um Im cos(ωt − ϕ).	(2.46)
			2
2

Практическое значение представляет не мгновенное значение мощности, а среднее за период, которое обозначим Р. Оно равно:

P =	1	Um Im cos ϕ,	(2.47)
	2

где cos ϕ =	R	.
где cos ϕ =		.
	Z
(2.48)
Учтем, что			Um		= Im :
Учтем, что			Z		= Im :
			Z
						P =	RIm	2		.		(2.49)
						P =	2			.		(2.49)
							2
Такую же мощность развивает и постоянный ток
							I =		Im		.	(2.50)
							I =				.	(2.50)
								2
Величина ID =					Im	называется действующим (эффективным) значением
Величина ID =				2		называется действующим (эффективным) значением
				2

силы тока, а U D = U2m - действующим (эффективным) значением напряже-

ния.

Тогда

P =UD ID cos ϕ.

(2.51)

Множитель соs ϕ называют коэффициентом мощности. В технике цепи рассчитывают так, чтобы соs ϕ был как можно больше. При малом соs ϕ для выделения в цепи необходимой мощности нужно пропускать ток большей силы, что приводит к возрастанию потерь в подводящих проводах.

Вопросы для самопроверки

1.От чего зависит индуктивное сопротивление? емкостное сопротивление?

2.Что такое реактивное сопротивление?

3.Запишите формулу для расчета мощности в цепи переменного тока.

4.От чего зависит коэффициент мощности?

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.02.2016879.05 Кб151_el-mash-spets-nazn-lab-rab.pdf
#
16.02.2016952.62 Кб551_elektrodinamika.pdf
#
16.02.20165.12 Mб2521_elektroenergetika-1-ispr.pdf
#
16.02.20162.31 Mб701_elektromehanika.pdf
#
16.02.20162.34 Mб321_fizika_ch-2umk-2.pdf
#
16.02.20162.06 Mб681_kolebaniya-i-volnyi--umknovoe1.pdf
#
16.02.20161.71 Mб321_matematika-ch--1,-2-y-semestr-2009-11-09.pdf
#
16.02.2016366.65 Кб101_praktika-doc.pdf
#
16.02.20161.27 Mб1781_sbornik-kontrolnih-rabot-po-fizike.pdf
#
16.02.20161.09 Mб261_sotsiologiya-svodnyiy-fayl-2010-03-22.pdf
#
16.02.20162.53 Mб241_tekctumk.pdf