Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северо-Западный государственный заочный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Теория литейных процессов том2.pdf

Скачиваний:

355

Добавлен:

16.02.2016

Размер:

2.4 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

4.Какие параметры определяют кинетику процесса кристаллизации?

5.Каков механизм столбчатой (дендритной) кристаллизации?

6.Назовите характерные зоны кристаллического строения слитка.

7.Каковы причины ликвационных явлений при кристаллизации?

8.Назовите основные виды ликвации в отливках.

9.Приведите классификацию модификаторов.

10.Каков механизм воздействия на структуру модификаторов I рода? II рода?

11.Опишите особенности кристаллизации и модифицирования эвтектик.

Раздел 6. ТЕПЛОВЫЕ ПРОЦЕССЫ. ЗАТВЕРДЕВАНИЕ ОТЛИВОК

Тема 6.1. Общие сведения о затвердевании

Основные условные обозначения

1.Теплофизические коэффициенты

a =	λ
		- коэффициент температуропроводности, м2/ч;
	Cγ	- коэффициент температуропроводности, м2/ч;
в =	λСγ - коэффициент аккумуляции тепла, ккал		1		;
		м2	час	2	0 C

С – удельная теплоемкость, ккалкг 0 C ;

Сэф – эффективная удельная теплоемкость, ккал/кг;

λ− коэффициент теплопроводности, ккал м2 час 0 C ;

γ− удельный вес, кг/м3;

ρ − удельная теплота кристаллизации, ккал/кг;

ρэф. – эффективная удельная теплота кристаллизации, ккал/кг;

ρсп. – спектральная теплота кристаллизации, ккалкг 0 C ;

ρсп.ср. – среднее значение спектральной теплоты кристаллизации,

ккалкг 0 C ;

ρсп. эф. – эффективная спектральная теплота кристаллизации,

ккалкг 0 C ;

ρэф.ср. – среднее значение эффективной спектральной теплоты кристаллизации, ккалкг 0 C ;

αm − коэффициент линейного расширения, 10/с;

βж − коэффициент линейного расширения, 10/с;

μс − коэффициент вязкости, кг с/м2;

α1 − коэффициент теплоотдачи на поверхности отливки,

ккал м2 час 0 C ;

α2 − коэффициент теплоотдачи на внутренней поверхности формы,

ккал м2 час 0 C ;

α3 − коэффициент теплоотдачи на внешней поверхности формы,

ккал м2 час 0 C ;

β − коэффициент теплоотдачи через зазор между отливкой и формой,

ккал м2 час 0 C ;

2. Температуры

t – температура, 0С;

Т – абсолютная температура, 0С;

tкр – температура кристаллизации, 0С; tлик – температура ликвидуса, 0С;

tс и tокр – температура окружающей среды, 0С; t1 нач – начальная температура отливки, 0С; t2 нач – начальная температура формы, 0С;

ϑ − температура, отсчитываемая от температуры окружающей среды или начальной температуры формы, 0С.

3. Размеры

Х1 – половина толщины плоской отливки или радиус цилиндрической и шаровой отливки, м; Х2 – толщина стенки формы, м;

Хкр – толщина слоя краски или обмазки, м; Хзаз – толщина зазора между отливкой и формой, м; ξ − толщина твердой корки, м;

ξ1 − толщина корки, образовавшейся к концу первой стадии процесса, м;

ξ2 − толщина корки, образовавшейся к концу второй стадии процесса, м;

R = VF − приведенный размер, м;

F – площадь, м2;

V – объем, м3;

ν − текущий объем; х, у, z – координаты.

4. Время

τ – время, ч;

τ0 – время течения металла до рассматриваемого сечения формы, ч;

τ1 – время, прошедшее от начала заливки до окончания первой стадии процесса, ч; τ2 – время, прошедшее от начала заливки до окончания второй стадии процесса, ч;

τ3 – время, прошедшее от начала заливки до окончания третьей стадии процесса, ч; τ4 – время, прошедшее от начала заливки до окончания четвертой ста-

дии процесса, ч.

5. Индексы

1 – обозначает принадлежность рассматриваемой величины к отливке;

2 – то же к форме; заз – то же к зазору;

с – то же к окружающей среде или к жидкому металлу; ′ – штрих вверху означает принадлежность теплофизической величины к металлу в жидком состоянии.

Некоторые вопросы теории теплообмена

Законы Ньютона, Стефана – Больцмана и Фурье

В общем случае теплообмен может осуществляться теплопроводностью (кондукцией), конвекцией и излучением. Два вида теплообмена – теплопроводность и конвекция – обычно объединяются в понятии теп-

лообмена соприкосновением. Процесс теплообмена излучением может протекать без наличия вещественной среды между телами. Внутри жидкости и газа теплота передается соприкосновением. Распространение тепла в твердом теле происходит вследствие теплопроводности.

Теплообмен соприкосновением (на поверхности тела) описывается

уравнением закона Ньютона
qc = αc t = αc(tn − tc),	(6.1)

где qс – удельный тепловой поток, Вт/(м2 К); αс – коэффициент теплоот-

дачи соприкосновением, Вт/(м2 К); t – температурный напор на поверхности тела, 0С.

t = tn – tc, 0С,

где tn и tc – температуры поверхности тела и окружающей среды, 0С. Полное количество теплоты, связано с удельным тепловым пото-

ком соотношением, Дж

dQc = qc F dτ, (6.2)

где F – площадь поверхности тела, омываемая средой, м2; dτ − элементарный отрезок времени, ч.

Теплообмен лучеиспусканием на поверхности одиночного абсолютно черного тела описывается уравнением закона Стефана – Больцмана

q		= С			Т	n	4
	л		О					,	(6.3)
				100

где С0 – коэффициент лучеиспускания абсолютно черного тела (С0= 4,9 Вт/(м2 К4)); Тп – абсолютная температура поверхности, К.

Для реального серого тела уравнение (6.3) приобретает вид

					Т	n	4			Т	п	4
q	л	= АС	О					= С					,	(6.4)
				100					100

где А – поглощательная способность (степень черноты тела); С – коэффициент излучения реального (серого) тела, Вт/(м2 К4).

	66
С = АС0.	(6.5)

Удельный тепловой поток при теплообмене между двумя неограниченными параллельными стенками, а также когда второе тело с поверхностью F2 охватывает первое тело, ограниченное выпуклой поверхностью F1, подсчитывается по формуле

											4				Т				4
q		= Сп			Т				1						Т	2
	л								1			−				2				,	(6.6)
							100					−		100
							100							100


где Сп – приведенный коэффициент														лучеиспускания							системы тел
Вт/(м2 К4); Т1 и Т2 – их абсолютные температуры, К.
Для параллельных пластин
Сn		=					1
Сn		=	1		+		1			−	1 .										(6.7)
			1				1				1 .										(6.7)
			С			С		2			С	0
			С			С					С
			1
Для системы тел, из которых одно охватывает другое
Сn		=							1
Сn		=	1				F1				1				1			,			(6.8)
																		,			(6.8)
				+									−
			С	+									−
			С			F				C		2			C		0
			1				2					2					0

где С1 и С2 – коэффициенты лучеиспускания первого и второго тел, Вт/(м2 К4).

Распространение тепла в твердом теле описывается уравнением закона теплопроводности Фурье, МВт/м2

q = −λ ∂∂t , n

где λ − коэффициент теплопроводности, Вт/(м2 К);

ратуры, К/м.

(6.9)

∂∂nt − градиент темпе-

Теплопередача через стенку

Рассмотрим процесс теплопередачи через неограниченную плоскую стенку, обладающую толщиной Х и коэффициентом теплопроводности λ и разделяющую среды 1 и 2 с разными температурами t1С и t2С и коэффициентами теплопередачи α1 и α2 (рис. 6.1). Режим стационарный (t1с > t2с).

Рис. 6.1. Схема теплопередачи через плоскую стенку

В рассматриваемых условиях количество теплоты подсчитывается по формуле

q =			t1C −t2C
q =		1 + X +			1	(6.10)
		1 + X +			1

	α1			λ	α2

или по одной из формул

q =α1 (t1C −t1П );

	λ		(6.11)
q =		(t1П −t2 П );
	X

q = α2 (t2 П −t2С ) .

Распределение температуры в сечении стенки (заштрихованная область) отвечает уравнению прямой линии:

t = t

−

−t

)

(6.12)

1П

2 П

В выражении (6.10)

представляет собою термическое сопротив-

ление стенки, величины

− термическое сопротивление теплоот-

даче, а сумма

− полное термическое сопротивление теп-

лопередаче.

Величина

К =

1 + X + 1

(6.13)

α1

α2

называется коэффициентом теплопередачи, Вт/(м2 К);

полным

термическим сопротивлением теплопередаче.

Разности температур t1с – t1п и t2п – t2с называются температурными напорами и обозначаются через 1t и 2t, разность t1п – t2п называется температурным перепадом и обозначается через δt.

В случае многослойной плоской стенки формула (6.10) принимает вид:

q =

t1C −t2C

(6.14)

i=n

+∑

i=1

Величину теплового потока в случае теплопередачи через цилиндрическую стенку (трубу) определяют по формуле Вт/(м2 К),

ql =			t1C −t2C
ql =	1	+	1 ln r2	+	1		,	(6.15)
	1	+	1 ln r2	+	1

	2πrα 2πλ r				2πr α	2
	1	1	1		2	2

где ql – тепловой поток, отнесенный к единице длины l трубы; r1 и r2 – радиусы внутренней и наружной поверхности трубы, м.

Распределение температуры, 0С, в сечении цилиндрической стенки определяется логарифмической кривой вида

		ln		r
t = t	−	ln		r1	(t	−t		)
				r1
			r2				2 П		,	(6.16)
1П		ln	r2		1П		2 П		,	(6.16)
		ln

где r1 < r < r2.

Если t2C > t1C, то расчетные формулы (6.15) и (6.16) для данного случая приобретают вид

ql =				t1C −t1C
ql =	1		+	1	ln	r2	+	1
	1			1		r2		1
	2πrα			2πλ		r		2πrα	2
	2πrα			2πλ		r		2πrα
	1	1			1			2

ln r2

и t = t2 П − ln rr2 (t2 П −t1П ). (6.17) r1

Тепловой поток, Вт, для шаровой стенки находится по формуле (t1C

> t2C)

Q =				t1C −t2C								τ .
Q =				1		1		1		1		τ .	(6.18)
	1		+	1		1	−	1	+	1
2			+				−		+	2
2				4πλ						2
	4πr1	α1		4πλ	r1			r2		4πr2	α2

Распределение температуры в сечении шаровой стенки отвечает уравнению гиперболы

−

t = t

−

− t

2 П

)

(6.19)

1 П

−

1 П

Если температура наружной среды превышает температуру внутренней (t2C > t1C), то уравнения (6.18) и (6.19) примут для шаровой вид стенки

Q =

t2C −t1C

(6.20)

−

4πr2α

4πλ

4πr2α

−

t = t

2 П

−

2 П

− t

1П

)

(6.21)

−

В качестве примера на рис. 6.2 изображены кривые распределения температуры в сечении плоской, цилиндрической и шаровой стенок для

случаев, когда t1с > t2с и t1с < t2с; отношение rr2 принято равным 2. Ход

кривых наглядно свидетельствует о существенном влиянии конфигурации на температурное поле стенки.

Рис. 6.2. Распределение температуры в плоской (прямые 1 и 4), цилиндрической (кривые 2 и 5) и шаровой (кривые 3 и 6) стенках при

различном направлении теплового потока

Анализируя формулы (6.16) – (6.21), можно сделать вывод о том, что при толщине Х = r2 – r1, когда она много меньше радиуса r1 кривизны, стенка любой конфигурации в тепловом отношении (имеются в виду температурное поле стенки и величина проходящего теплового потока) не отличается от плоской. Стенка обладает малой кривизной поверхности, если соблюдается требование

Хr <<1 (толщина стенки много меньше радиуса кривизны). (6.22)

Любая кривая стенка практически не отличается от плоской, если радиус кривизны в 5 - 10 раз превышает толщину (как при стационарном, так и при нестационарном распространении тепла).

Рассмотрим еще одно важное свойство температурного поля твердого тела при стационарных и нестационарных условиях теплообмена.

Предположим, что изучается нестационарный режим охлаждения тела, обладающего произвольной конфигурацией.

Рис. 6.3. Построение направляющей точки для нестационарного режима

На поверхности тела в некоторой точке В (рис. 6.3) проведена касательная к кривой распределения температуры в его сечении (температурная кривая соответствует линии ВД). Из треугольника АНВ находим

tgϕ = BA = tn −tc . AH AH

С другой стороны, известно, что тангенс угла наклона касательной к точке В равен соответствующей производной. Имеем

tgϕ		∂t
	= −		,	(6.23)

		∂n n

где n – нормаль; индекс n указывает на то, что производная взята для поверхности тела.

К поверхности тела из его внутренних слоев подходит количество теплоты, переданной теплопроводностью (закон Фурье),

	∂t
q = −λ		.	(6.24)

	∂n n

В окружающую среду с поверхности теряется количество теплоты:

	q =α (tn −tc ).					(6.25)
	∂t	=α (t		)
Очевидно,	− λ		−t		.	(6.26)

		n	c
	∂n n

Подставив в (6.23) значения соответствующих величин, выраженных через tgϕ, найдем

АН =	λ .	(6.27)
	α

Отсюда следует, что расстояние от поверхности тела до точки Н определяется только величинами λ и α и не зависит от остальных условий процесса (температур поверхности и среды, размеров тела и т. д.). Через точку Н, которая называется направляющей, проходят касательные к кривым распределения температуры в сечении тела для любого момента времени. Направляющая точка Н лежит на уровне температуры tс окружающей среды, а точка касания располагается на поверхности тела. Это замечательное свойство температурного поля тела будет широко использовано в дальнейшем.

Критерий Био

Если процесс распространения тепла происходит в плоской стенке при стационарном режиме, то картина, изображенная на рис. 6.3, заметно упростится, так как распределение температуры в сечении плоской стенки отвечает уравнению прямой линии, и, следовательно, касательная к прямой будет являться ее продолжением (рис. 6.4).

Рис. 6.4. Построение направляющей точки для плоской стенки при стационарном режиме

Точки Д и Е (см. рис. 6.3) сольются: из подобных треугольников АНВ и СВД (рис. 6.4) найдем

	tgϕ	=	tП − tC		=		tO − tП
	tgϕ	=		λ	=
				λ				X
или				α						(6.28)
или	α Х =			tO − tП		.				(6.28)
				tO − tП

	λ			tП − tC
	Безразмерный комплекс величины							α	Х	называется критерием Био
								λ
и обозначается через Bi. Имеем:
	Bi =	α Х .								(6.29)
		λ

Разность tO – tП представляет собой перепад температуры в сечении тела, а разность tП – tС – температурный напор на поверхности тела. Первая разность обозначается через δt, вторая через t. Следовательно, окончательно будем иметь

Bi =	δt
Bi =	t .	(6.30)

Вслучае теплопередачи через плоскую стенку при стационарном режиме критерий Bi численно равен отношению температурного перепада в теле к температурному напору на поверхности.

Вобщем случае нестационарного режима и тела более сложной конфигурации критерий Био уже не равен точно отношению перепада к напору, так как при этом отрезок СD оказывается неравным отрезку СЕ (см. рис. 6.3). Однако и в этом случае критерий Био сохраняет смысл меры указанного отношения. Имеем

Bi ≈	δt
Bi ≈	t .	(6.31)

Знак ≈ означает, что рассматриваются величины одного порядка (различающиеся менее, чем в 10 раз).

Критерий Био является одной из наиболее важных величин теории теплопроводности: он характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Критерий Био содержит суммарный коэффициент теплоотдачи α и теплопроводности λ, относящийся к твердому телу.

Величину Bi можно переписать следующим образом


α		Х
α	Х =	λ
Bi = λ	Х =	1 .	(6.32)
Bi = λ		1 .	(6.32)

Как видим, критерий Bi имеет смысл отношения термического со-

противления	Х	1
		тела к термическому сопротивлению		на поверхно-
	λ		α

сти. В зависимости от конкретного численного значения критерия Bi в решения могут быть внесены те или иные упрощения. В этом случае надо различать три типичных случая теплообмена (рис. 6.5).

Рис. 6.5. Распределение температуры в сечении тела в случае малой, средней и большой интенсивности теплообмена

Первый случай (рис. 6.5, а) характеризуется малой относительной интенсивностью теплообмена, что соответствует условию

Bi << 1.

Знак << означает, что левая часть неравенства «много меньше» его правой части. Правая часть равна единице, следовательно, левая часть, строго говоря, должна стремиться к нулю. Практически соблюдение подобного рода неравенств осуществляется в том случае, когда в левой и правой части содержатся величины разного порядка (различающиеся в 10 и более раз).

Малое значение Bi может быть получено за счет малого термическо-

го сопротивления λ тела или большого термического сопротивления

α на поверхности. При этом направляющая точка стоит далеко от по-

верхности и температурный перепад (δt) внутри тела становится пре-

небрежимо малым по сравнению с температурным напором t. При этом достигается наибольшее упрощение задачи, так как тепловое состояние тела в целом вполне определяется одним значением температуры (tc ≈ tп).

Второй случай (рис. 6.5, в), противоположный предыдущему, характеризуется большой интенсивностью теплообмена тела с окружающей средой, что соответствует условию:

Bi >> 1.

Знак >> означает, что левая часть неравенства «много больше» ее правой части (обе части неравенства различаются между собой в 10 и более раз). При этом направляющая точка находится вблизи поверхности тела и, следовательно, появляется возможность пренебречь температурным напором t. Иначе говоря, этот случай характеризуется тем, что температура поверхности тела становится практически равной температуре окружающей среды (tп ≈ tс).

Третий случай (рис. 6.5, б), характеризуется средними значениями Био:

Bi ≈ 1.

В этих условиях температурный перепад является величиной того же порядка, что и температурный напор. Ни тем, ни другим пренебречь нельзя, потому задачу приходиться решать в всей ее фактической сложности.

Вышеизложенное позволяет произвести классификацию условий литья, а также выполнить качественный контроль процесса формирования отливки.

Классификация условий литья

Условия литья должны классифицироваться по тем признакам явления, которые не могут быть одновременно охвачены теоретическим анализом. Иными словами, каждый класс условий должен отличаться от других классов совокупностью признаков, требующих особого теоретического подхода.

Общими признаками являются относительные геометрические характеристики системы «отливка – зазор – форма». Выбор геометрических свойств в качестве классификационных признаков системы обусловлен следующими соображениями.

Для процесса теплообмена между отливкой и формой важное значение имеет аккумулирующая способность отдельных элементов системы «отливка – зазор – форма». Под аккумулирующей способностью понимается количество теплоты, которое потеряет или приобретет тело, если его температура изменится на определенную величину. Аккумулирующая способность определяется массой и теплоемкостью тела. Однако при оценке относительных свойств отдельных элементов системы с помощью критериальных зависимостей (отношений) в виде неравенств точное определение аккумулирующей способности отливки, зазора и формы знать не обязательно. С указанной целью вполне допустимо пользоваться массами, объемами или даже размерами (толщинами) рассматриваемых тел.

В качестве размера отливки выберем величину Х1 (половина толщины плоской отливки, радиус цилиндрической или шаровой отливки).

Толщину зазора обозначим через Хзаз. Под зазором будем условно понимать неметаллическую прослойку, заключенную между отливкой и формой. В случае кокиля зазор состоит из слоя краски или смазки, газовой прослойки и слоя окислов. В случае двухслойной формы сюда же будет относиться прослойка из песчано-глиняной смеси. Толщину стенки кокиля обозначим через Х2.

Каждая из величин Х1, Хзаз и Х2 может приобретать на практике самые различные значения. Определенные сочетания относительных размеров отливки, зазора и формы приводят к характерным условиям литья, требующим особого теоретического подхода. Рассмотрим подробнее все наиболее характерные случаи литья.

Тонкостенный кокиль. Первый частный случай теплообмена между отливкой и формой характеризуется тем, что толщины зазора и кокиля пренебрежимо малы по сравнению с толщиной отливки. Математически эти требования можно записать следующим образом:


	Хзаз	<<1 и		Х2	<<1.	(6.33)
	Хзаз
				Х1
	Х1			Х1
Из них непосредственно вытекает неравенство
	Хзаз + Х2		<<1.			(6.34)
	Х1		<<1.			(6.34)
	Х1

Из приведенных неравенств следует, что при затвердевании отливки количество теплоты, аккумулированной зазором и кокилем, пренебрежимо мало по сравнению с количеством теплоты, которую теряет отливка. В результате нагрев зазора и кокиля практически не может сказаться на процессе затвердевания отливки. Роль кокиля целиком сводится к передаче тепла от отливки окружающей среде. Это обстоятельство имеет чрезвычайно важное значение для теории, так как позволяет заменить эффект действия зазора и кокиля влиянием определенного термического сопротивления на поверхности отливки. Вместо сложной

системы «отливка – зазор – форма» допустимо рассматривать одну лишь отливку, которая охлаждается в окружающей среде, обладающей температурой tс с коэффициентом теплопередачи α1.

Массивный кокиль. Если аккумулирующая способность зазора ничтожно мала, а аккумулирующая способность кокиля соизмерима с аккумулирующей способностью отливки, при затвердевании металла часть выделившегося тепла будет аккумулирована кокилем, а часть потеряна в окружающую среду. Соответствующие условия математически записываются следующим образом:

	Хзаз	<<1 и		Х2	≈1.	(6.35)
	Х1			Х1

Отсюда можно получить соотношение
	Хзаз	+ Х2	≈1 .			(6.36)

	Х1

При решении данной задачи можно пренебречь количеством теплоты, аккумулированной зазором. Однако аккумулирующей способностью кокиля, а также потерями тепла в окружающую среду пренебречь нельзя.

Двухслойная форма. Третий случай соответствует условиям, когда аккумулирующая способность зазора и кокиля соизмерима с аккумулирующей способностью отливки. Имеем

Хзаз	≈1;	Х2	≈1;	Хзаз + Х2	≈1 .	(6.37)
		Х1
Х1				Х1

В рассматриваемом случае аккумулирующая способность зазора (состоящего из обмазки или слоя формовочной смеси) оказывает существенное влияние на процесс затвердевания отливки. При этом нельзя пренебречь ни влиянием теплоаккумулирующей способности зазора, ни влиянием теплоаккумулирующей способности кокиля. Теплообмен при-

ходится рассматривать как процесс взаимодействия между отливкой и двухслойной формой.

Неметаллическая форма. Четвертый распространенный случай, когда аккумулирующая способность зазора много больше аккумулирующей способности отливки, характеризуется требованием

Хзаз	>>1 .	(6.38)

Х1

При этом теряемая отливкой теплота практически полностью аккумулируется материалом «зазора» (понятие «зазор» имеет условный смысл, так как зазор фактически вырождается в «неограниченную» форму).

Рассматриваемые условия теплообмена очень часто встречаются на практике. При решении поставленной задачи упрощение достигается за счет пренебрежения количеством теплоты, теряемой формой с внешней поверхности. Кроме того, ряд других упрощений связан со специфическими особенностями процесса распределения тепла в неметаллической форме. Решение данной задачи будет приведено в дальнейшем.

Классификация условий литья представлена в табл. 6.1.

Таблица 6.1

Классификация условий литья по признаку относительных размеров отливки, зазора и формы

Анализ температурного поля металла, охлаждающегося в литейной форме

Отливка при своем охлаждении в форме проходит через ряд последовательных состояний, которые зависят от характера измерения температуры и других свойств металла.

Можно отметить пять основных стадий охлаждения отливки:

−первая стадия соответствует заполнению формы расплавленным металлом;

−вторая – охлаждению жидкого металла после окончания заливки;

−третья – затвердеванию металла;

−четвертая стадия – охлаждению в форме полностью затвердевшей отливки;

−пятая – охлаждению отливки после удаления из формы.

Четкое разграничение отдельных стадий позволяет составить наиболее эффективную систему дифференциальных уравнений процесса и соответствующие им условия однозначимости и затем решать поставленную задачу о затвердевании отливки.

Заполнение формы. Первая стадия охлаждения отливки связана с заполнением формы расплавленным металлом. Началом первой стадии надо считать момент соприкосновения первых капель расплава с формой, концом – момент окончания заливки. Длительность первой стадии τ1 зависит от гидродинамических условий процесса и часто может быть задана технологом.

В течение первой стадии происходит охлаждение жидкого металла и нагрев формы. В процессе охлаждения расплава может произойти его затвердевание (лучше не допускать этого). Все это должно быть учтено при составлении дифференциального уравнения процесса для первой стадии:

−τ1 − длительность первой стадии;

−ξ1 или V1 – толщина корки или объем затвердевшего металла.

Величины τ1 и ξ1 (или V1) являются начальными для второй стадии процесса.

Отвод теплоты перегрева. Во второй стадии происходит отвод теплоты перегрева от расплавленного металла. Этот процесс также может сопровождаться затвердеванием отливки. Во второй стадии, в отличие

от первой, в жидком металле отсутствует вынужденная конвекция, но может происходить более или менее интенсивная естественная конвекция, оказывающая влияние на температурное поле отливки.

Признаком, по которому определяется конец второй стадии, является достижение средней частью отливки (затвердевающей в последнюю очередь) температуры затвердевания (если металл кристаллизуется при постоянной температуре) или температуры ликвидуса (если металл кристаллизуется в интервале температур). Длительность двух первых стадий формирования отливки составляет τ2, толщина корки – ξ2 (V2).

Затвердевание металла. Третья стадия охлаждения отливки соответствует затвердеванию металла. В течение этого процесса происходит формирование отливки.

Во время затвердевания металла фронт кристаллизации перемещается от периферии внутрь отливки. Если металл затвердевает при постоянной температуре (чистые металлы, эвтектические сплавы), то отливка в каждый данный момент времени состоит из двух зон – твердой и жидкой, причем жидкая зона обладает температурой кристаллизации. Если металл затвердевает в интервале температур (сплавы), то в отливке можно различать три зоны – твердую, жидкую и переходную (жидкотвердую). В последнем случае затвердевание металла сопровождается понижением температуры от ликвидуса до солидуса.

В жидком ядре затвердевающей отливки имеется лишь слабая естественная конвекция, обусловленная неоднородным составом металла ядра и движением так называемых подвижных кристаллов, если таковые имеются.

Конец третьей стадии определяется по признаку начала снижения температуры центральной части отливки ниже температуры кристаллизации или солидуса.

Общая длительность первых трех стадий охлаждения отливки составляет τ3. В момент полного затвердевания отливки (при τ=τ3) толщи-

на затвердеваний корки ξ3=Х1 и V=V1 (где Х1 – половина толщины плоской отливки и радиус цилиндрической или шаровой отливки, V3 – ее объем). Величины τ3 и Х1 (V3) входят в состав начальных условий четвертой стадии.

Охлаждение в форме полностью затвердевшей отливки. После затвердевания всего металла начинается четвертая стадия – охлаждение в форме полностью затвердевшей отливки. При этом происходят определенные фазовые и структурные превращения, изменяются термические напряжения в металле, появляются горячие трещины и т. д. Четвертая стадия заканчивается в момент удаления отливки из формы. Концу четвертой стадии соответствует время τ4 и определенное температурное поле отливки. Условия, сложившиеся в момент окончания четвертой стадии, являются начальными для пятой стадии.

Охлаждение отливки вне формы. После удаления отливки из формы происходит ее дальнейшее охлаждение в окружающей среде (пятая стадия) – в воздухе цеха, в специальных колодцах, печах и других устройствах. В материале отливки могут происходить различные структурные превращения, изменяться напряжение и т. д. Заканчивается эта стадия при достижении комнатной температуры.

Различные стадии процесса охлаждения отливки наглядно представлены графически на рис. 6.6, на котором изображена зависимость температуры центральной (затвердевающей в последнюю очередь) части отливки от времени.

Напомним, что граница между стадиями I и II определяется длительностью процесса заливки и поэтому не зависит от хода температурной кривой. Эта длительность выбирается технологом из дополнительных соображений. Стадия IV отделяется от стадии V моментом τ4 уда-

ления отливки из формы. Выбор этого момента также целиком зависит от технолога.

Рис. 6.6. Схема расчленения процесса охлаждения отливки на стадии: а – металл кристаллизуется при постоянной температуре; б - металл кристаллизуется в интервале температур. Номера стадий

отмечены римскими цифрами

В точках τ1 и τ4 может наблюдаться некоторый перегиб температурных кривых. Заметим, что температурная кривая на рис. 6.6, б на участке затвердевания АВ может иметь различный ход в зависимости от конкретных свойств кристаллизующегося сплава.

Частные случаи затвердевания отливки

В отдельных случаях некоторые из перечисленных стадий процесса могут отсутствовать. Например, при заливке металла без перегрева или при длительной заливке, когда металл теряет свой перегрев еще в ста-

дии течения, отсутствует II стадия. Если отливки охлаждаются в форме до температуры цеха tС, то отсутствует V стадия и т. д.

В некоторых случаях влиянием отдельных стадий можно пренебречь ввиду их малой продолжительности. Например, при быстрой заливке металла в небольшие формы можно пренебречь влиянием I стадии (τ1 = 0). Если при этом перегрев металла невелик, то можно пренеб-

речь также и влиянием II стадии (τ1=τ2=0). Подобного рода условия часто встречаются на практике.

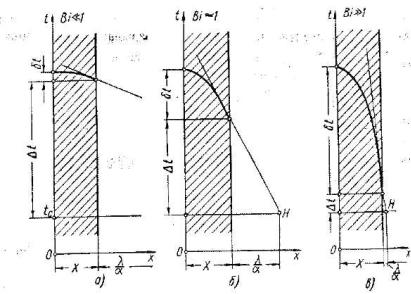
Рис. 6.7. Схема распределения температуры в сечении отливки при различной интенсивности теплообмена (металл кристаллизуется при

постоянной температуре tкр)

На рис. 6.7 приведена схема распределения температуры в сечении отливки при различных значениях интенсивности теплообмена (металл кристаллизуется при постоянной температуре tкр) и отдельные температурные кривые соответствуют различным моментам времени (аналогичная картина для твердого тела изображена на рис. 6.5). Толщина твердой корки ξ показана штриховкой для одного момента. Для других мо-

ментов величина ξ показана вертикальными волнистыми линиями. Для определенного момента обозначены величины температурного перепада δ1t и температурного напора 1t. В целом график охватывает все пять стадий охлаждения отливки (от τ=0 и t1=tзал до τ=∞ и t1=tс).

Из рис. 6.7 видно, что при средней (Bi≈1) и большой (Bi>>1) интенсивностях теплообмена наблюдается заметное взаимное наложение отдельных стадий процесса, что обусловлено наличием больших перепадов δ1t температуры в сечении отливки. Например, в момент τ, для кото-

рого штриховкой показана толщина ξ твердой корки, происходит отвод теплоты перегрева (или даже течение металла). Вместе с тем этот процесс одновременно сопровождается также затвердеванием отливки (образовалась корка толщиной ξ) и охлаждением затвердевающей корки ниже температуры tКР.

При относительно малой интенсивности теплообмена (Bi<<1) перепад температуры δ1t в сечении отливки чрезвычайно незначителен. Благодаря этому процесс отвода теплоты перегрева начинается (и заканчивается) по всей массе отливки одновременно. Процесс затвердевания происходит в условиях постоянства температуры жидкого ядра и образовавшейся корки. Практически одновременно начинается также процесс охлаждения полностью затвердевшего металла. Иными словами, любая последующая стадия начинается только после того, как закончилась предыдущая, и следовательно, каждую стадию можно изучать независимо от всех остальных (т. е. можно пренебречь взаимным наложением стадий).

Аналогичная картина получается также при затвердевании сплава в интервале температур (рис. 6.8). Разница между данным и предыдущим случаем заключается в том, что при наличии интервала tкр в отливке появляется переходная зона, содержащая одновременно жидкую фазу и выпавшие кристаллы. Ширина Δξкр переходной зоны возрастает по мере

уменьшения интенсивности теплообмена – она минимальна при Bi>>1 и охватывает весь объем отливки при Bi<<1.

Рис. 6.8. Схема распределения температуры в сечении отливки при различной интенсивности теплообмена (металл кристаллизуется в

интервале температур tкр)

Как и прежде (рис. 6.7), при средней (Bi≈1) и большой (Bi>>1) интенсивности теплообмена происходит заметное взаимное наложение различных стадий (отвод теплоты перегрева, затвердевание металла, охлаждение полностью затвердевшей корки). При малой интенсивности теплообмена (Bi<<1) наложением стадий можно пренебречь.

Особенность процесса затвердевания с малой интенсивностью охлаждения заключается в том, что благодаря наличию незначительного перепада температуры в сечении отливки выпадение твердой фазы происходит по всему объему металла практически одновременно (так называемое объемное затвердевание). При этом температура отливки равномерно и плавно понижается от tлик до tсол. Процесс затвердевания

начинается одновременно по всему объему металла после достижения температурой отливки значения tлик и заканчивается при температуре tсол (в условиях равновесного процесса). Как видим, при малой интенсивности теплообмена и наличии интервала температур кристаллизации попрежнему соблюдается правило независимости протекания отдельных стадий.

Рассмотренные частные случаи охлаждения отливки, связанные с возможностью пренебречь взаимным влиянием отдельных стадий процесса или обусловленные независимым протеканием отдельных стадий (при Bi<<1), представляют большой интерес, так как часто встречаются на практике и позволяют существенно упростить задачу.

Ясно, что самой важной стадией процесса формирования отливки является третья стадия (затвердевание металла). Эта стадия имеет место во всех случаях литья и может различаться только интенсивностью теплообмена. В соответствии с этим целесообразно выделить третью стадию процесса и изучить ее особо: необходимо получить универсальное математическое решение задачи о затвердевании металла. Полученное универсальное решение для третьей стадии можно будет затем использовать для всех частных условий литья.

Затвердевание плоской отливки при постоянной температуре кристаллизации

Постановка задачи. Будем считать, что отливка охлаждается в окружающей среде, обладающей постоянной температурой tС с коэффициентом теплопередачи α1. Величины tС и α1 определяются в зависимости от конкретных условий литья и являются известными и постоянными.

Требуется найти закон затвердевания отливки (закон продвижения фронта затвердевания во времени), линейную скорость затвердевания металла, температурное поле (включая скорость изменения температуры во времени) и количество потерянной теплоты.

Зададимся законом распределения температуры в сечении тела (отливки). В качестве температурной кривой будем использовать параболу n–го порядка. Применительно к затвердевшей корке отливки парабола имеет вид

					у	n
t = −(t	кр	− t	1п	)	у		+ t	кр ,	(6.39)
t = −(t		− t		)			+ t
					ξ
					ξ

где у – координата, отсчитываемая от фронта затвердевания в направлении к поверхности отливки; ξ − толщина корки, затвердевшей к мо-

менту τ; n – показатель, выбор которого подчиняется особым условиям.

Рис. 6.9. Схема распределения температуры в сечении отливки в моменты τ и τ + dτ (показано пунктиром)

Вместо координаты у можно применять координату х, отсчитываемую от поверхности отливки (в направлении к фронту затвердевания). Тогда получим (рис. 6.9):

						х	n
t = −(t	кр	− t	1п	) 1	−	х		+ t	кр ,	(6.40)
t = −(t		− t		) 1	−			+ t
						ξ
						ξ

где х = ξ − у.

Можно воспользоваться также координатой Z, отсчитываемой от середины отливки и направленной в сторону ее поверхности. Тогда уравнение температурного поля имеет вид:

1 −

t = −(t

кр

− t

1п

) 1

−

+ t

кр ,

(6.41)

где δ − относительная толщина затвердевшей корки:

δ =	ξ		.	(6.42)
	Х	1

Температура корки в момент τ соответствует BF. Температурная кривая для момента τ + dτ изображена пунктиром на рис. 6.9.

Расчетную формулу можно привести к безразмерному виду из (6.39)

или (6.40)

tкр − t			x n
		−			(6.43)

tкр −t1п	= 1			,
			ξ

так как у = ξ – х.

Формула (6.43) является основным выражением, по которому вычисляют температуру в сечении затвердевшей корки. Этой формулой можно пользоваться для отливки любой конфигурации, причем влияние конфигурации сказывается на величине показателя n. Подбирая показатель n, можно в каждом конкретном случае добиться того, чтобы полу-

ченное приближенное решение обладало удовлетворительной точностью.

Как видим из рис. 6.10, придавая n различные значения, можно получить серию температурных кривых, которые почти всегда позволяют с удовлетворительной для практических целей точностью приближенно описать действительную температурную кривую.

Рис. 6.10. Распределение температуры в сечении затвердевшей корки при различных показателях n: 1 – показатель n = 1/4;

2 – показатель n = 1/3; 3 – показатель n = 1/2; 4 – показатель n = 1; 5 – показатель n = 2; 6 – показатель n = 3; 7 – показатель n = 4

Чтобы упростить расчет по формуле (6.43), в табл. 6.2 приведены

tкр −t

значения безразмерной температуры tкр −t1п в зависимости от показа-

теля n и безразмерной координаты ξ для практических расчетов.

Таблица 6.2

tкр −t

Значения безразмерной температуры tкр −t1n в зависимости от

	показателя n и относительной координаты								x	(см. (6.43))
	показателя n и относительной координаты								ξ	(см. (6.43))

n						x/ξ

	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7		0,8	0,9	1
	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7		0,8	0,9	1

0,05	1,000	0,995	0,989	0,982	0,975	0,966	0,955	0,942		0,923	0,891	0

0,10	1,000	0,989	0,978	0,965	0,950	0,933	0,912	0,886		0,851	0,794	0

0,15	1,000	0,984	0,967	0,948	0,926	0,901	0,872	0,835		0,785	0,708	0

0,20	1,000	0,979	0,956	0,931	0,903	0,871	0,833	0,786		0,725	0,631	0

0,25	1,000	0,974	0,946	0,915	0,880	0,841	0,795	0,740		0,669	0,562	0

0,30	1,000	0,969	0,935	0,898	0,858	0,812	0,760	0,697		0,617	0,501	0

0,35	1,000	0,964	0,925	0,883	0,836	0,784	0,726	0,656		0,596	0,447	0

0,40	1,000	0,959	0,914	0,867	0,815	0,758	0,693	0,618		0,525	0,398	0

0,45	1,000	0,954	0,904	0,852	0,795	0,732	0,662	0,582		0,485	0,355	0

0,50	1,000	0,949	0,894	0,837	0,775	0,707	0,632	0,548		0,447	0,316	0

0,55	1,000	0,944	0,884	0,822	0,755	0,683	0,604	0,516		0,413	0,282	0

0,60	1,000	0,939	0,875	0,807	0,736	0,660	0,577	0,486		0,381	0,251	0

0,65	1,000	0,934	0,865	0,793	0,717	0,637	0,551	0,457		0,351	0,224	0

0,70	1,000	0,929	0,855	0,779	0,699	0,616	0,527	0,430		0,324	0,199	0

0,75	1,000	0,924	0,846	0,765	0,682	0,595	0,503	0,405		0,299	0,178	0

0,80	1,000	0,919	0,837	0,752	0,665	0,574	0,480	0,382		0,276	0,158	0

0,85	1,000	0,914	0,827	0,738	0,648	0,555	0,459	0,359		0,255	0,141	0

0,90	1,000	0,909	0,818	0,725	0,632	0,536	0,438	0,338		0,235	0,126	0

0,95	1,000	0,905	0,809	0,712	0,616	0,518	0,419	0,318		0,217	0,112	0

1,00	1,000	0,900	0,800	0,700	0,600	0,500	0,400	0,300		0,200	0,100	0

1,05	1,000	0,895	0,791	0,688	0,585	0,483	0,382	0,232		0,184	0,089	0

1,10	1,000	0,890	0,782	0,675	0,570	0,467	0,365	0,266		0,170	0,079	0

1,15	1,000	0,886	0,774	0,664	0,556	0,451	0,349	0,250		0,157	0,071	0

1,20	1,000	0,881	0,765	0,652	0,542	0,435	0,333	0,236		0,145	0,063	0

Продолжение табл. 6.2

n						x/ξ

	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1

1,25	1,000	0,876	0,757	0,640	0,528	0,420	0,318	0,222	0,134	0,056	0

1,30	1,000	0,872	0,748	0,629	0,515	0,406	0,304	0,209	0,123	0,050	0

1,35	1,000	0,867	0,737	0,618	0,502	0,392	0,290	0,197	0,114	0,045	0

1,40	1,000	0,863	0,732	0,607	0,489	0,379	0,277	0,185	0,105	0,040	0

1,45	1,000	0,858	0,724	0,596	0,477	0,366	0,265	0,174	0,097	0,035	0

1,50	1,000	0,853	0,715	0,586	0,465	0,354	0,253	0,164	0,089	0,032	0

1,55	1,000	0,849	0,708	0,575	0,453	0,341	0,242	0,155	0,082	0,028	0

1,60	1,000	0,845	0,700	0,565	0,442	0,330	0,231	0,146	0,076	0,025	0

1,65	1,000	0,840	0,692	0,555	0,430	0,319	0,221	0,137	0,070	0,022	0

1,70	1,000	0,836	0,684	0,545	0,420	0,308	0,211	0,129	0,065	0,020	0

1,75	1,000	0,831	0,677	0,536	0,409	0,297	0,201	0,122	0,060	0,018		0

1,80	1,000	0,827	0,669	0,526	0,399	0,287	0,192	0,114	0,055	0,016		0

1,85	1,000	0,823	0,662	0,517	0,389	0,277	0,184	0,108	0,051	0,014		0

1,90	1,000	0,818	0,654	0,508	0,379	0,268	0,175	0,101	0,047	0,013		0

1,95	1,000	0,814	0,647	0,499	0,369	0,259	0,167	0,096	0,043	0,011		0

2,00	1,000	0,810	0,640	0,490	0,360	0,250	0,160	0,090	0,040	0,010		0

2,1	1,000	0,801	0,626	0,473	0,342	0,233	0,146	0,080	0,034	0,008		0

2,2	1,000	0,793	0,612	0,456	0,325	0,218	0,133	0,071	0,029	0,006		0

2,3	1,000	0,785	0,598	0,440	0,309	0,203	0,121	0,063	0,025	0,005		0

2,4	1,000	0,776	0,585	0,425	0,294	0,189	0,111	0,056	0,021	0,004		0

2,5	1,000	0,768	0,572	0,410	0,279	0,177	0,101	0,049	0,018	0,003		0

2,6	1,000	0,760	0,560	0,396	0,265	0,165	0,092	0,044	0,015	0,002		0

2,7	1,000	0,752	0,547	0,382	0,252	0,154	0,084	0,039	0,013	0,002		0

2,8	1,000	0,744	0,535	0,368	0,239	0,144	0,077	0,034	0,011	0,002		0

2,9	1,000	0,736	0,524	0,355	0,227	0,134	0,070	0,030	0,009	0,001		0

3,0	1,000	0,729	0,512	0,343	0,216	0,125	0,064	0,027	0,008	0,001		0

3,2	1,000	0,714	0,490	0,319	0,195	0,109	0,053	0,021	0,006	0,001		0

3,4	1,000	0,699	0,468	0,297	0,176	0,095	0,044	0,017	0,004	0,000		0

3,6	1,000	0,684	0,448	0,277	0,159	0,082	0,037	0,013	0,003	0,000		0

3,8	1,000	0,670	0,428	0,258	0,144	0,072	0,031	0,010	0,002	0,000		0

Окончание табл. 6.2

n						x/ξ

	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1

4,0	1,000	0,656	0,410	0,240	0,130	0,062	0,026	0,008	0,002	0,000		0

4,2	1,000	0,642	0,392	0,224	0,117	0,054	0,021	0,006	0,001	0,000		0

4,4	1,000	0,629	0,375	0,208	0,106	0,047	0,018	0,005	0,001	0,000		0

4,6	1,000	0,616	0,358	0,194	0,095	0,041	0,015	0,004	0,001	0,000		0

4,8	1,000	0,603	0,343	0,180	0,086	0,036	0,012	0,003	0,000	0,000		0

5,0	1,000	0,590	0,328	0,168	0,078	0,031	0,010	0,002	0,000	0,000		0

5,5	1,000	0,560	0,293	0,141	0,060	0,022	0,006	0,001	0,000	0,000		0

6,0	1,000	0,531	0,262	0,118	0,047	0,016	0,004	0,001	0,000	0,000		0

6,5	1,000	0,504	0,234	0,098	0,036	0,011	0,003	0,000	0,000	0,000		0

7,0	1,000	0,478	0,210	0,082	0,028	0,008	0,002	0,000	0,000	0,000		0

7,5	1,000	0,453	0,188	0,069	0,022	0,005	0,001	0,000	0,000	0,000		0

8,0	1,000	0,430	0,168	0,058	0,017	0,004	0,001	0,000	0,000	0,000		0

8,5	1,000	0,408	0,150	0,048	0,013	0,003	0,000	0,000	0,000	0,000		0

9,0	1,000	0,387	0,134	0,040	0,010	0,002	0,000	0,000	0,000	0,000		0

9,5	1,000	0,367	0,120	0,034	0,008	0,001	0,000	0,000	0,000	0,000		0

10,0	1,000	0,348	0,107	0,028	0,006	0,001	0,000	0,000	0,000	0,000		0

Закон затвердевания. Для нахождения закона продвижения фронта затвердевания в плоской отливке составим необходимое дифференциальное уравнение теплового баланса.

Количество теплоты dQ, теряемой отливкой с поверхности F1 за время dτ, должно быть равно количеству аккумулированной теплоты dQакк, выделяющейся в затвердевшей корке вследствие понижения ее температуры, и количеству теплоты dQкр кристаллизации

dQ = dQакк + dQкр. (6.44)

Найдем каждое из перечисленных количеств теплоты. Величина dQ определяется с помощью закона теплопроводности Фурье (6.9). Чтобы воспользоваться этой формулой, необходимо найти градиент темпера-

туры на поверхности отливки. Для этого продифференцируем уравнение температурной кривой (6.39) по у:

∂t

= −n (t

−t

)

уn−1

кр

1п

ξ n .

(6.45)

∂y

Для поверхности тела у = ξ (рис. 6.9).

Отсюда следует, что

∂t

tкр

−t1п

= −n

;

(6.46)

∂y n

∂t

tкр − t1п

dQ =

F1dτ = λ1n

F1dτ ,

(6.47)

−λ1

∂y n

где λ1 – теплопроводность затвердевшего тела.

Элементарное количество аккумулированной теплоты dQакк находится путем дифференцирования выражения для Qакк. Полное количество аккумулированной теплоты Qакк может быть определено по средней

температуре затвердевшей корки
Qакк. = Vγ1С1 (tкр – tср),				(6.48)
где V – объем затвердевшей корки; γ1 − удельный вес материала корки;
С1 – удельная теплоемкость материала корки;				tср – средняя по объему
температура в момент τ.
Для плоской отливки
V = F1ξ.				(6.49)
Средняя по объему корки температура может быть найдена путем
интегрирования уравнения температурной кривой:
tкр −tср =	∫ξ (tкр −t)dV1
	0
		ξ	,	(6.50)
		∫dV1

где dV1 – элементарный объем затвердевшей корки, обладающий температурой t.

Для плоской отливки величина dV1 = F1dy.

Подставляя в предыдущее выражение значение соответствующих величин, находим

∫

кр

−t

)

F dy

1п

tкр −tср =

∫F1dy

(6.51)

yn+1

tкр −t1п

−t

(n +1) ξn

кр

1п

Здесь переменной величиной являлась координата у. Интегрирование производилось в пределах толщины затвердевшей корки. Найденная разность температуры tкр – tср представляет собой среднее понижение температуры корки.

Подставляя эту разность температуры в выражение количества аккумулированной теплоты, будем иметь:

Q		=	1	F ξγ C	(t		−t	)	.	(6.52)
			n +1
	акк			1 1 1		кр	1п

На рис. 6.9 количество теплоты Qакк определяется площадью, заключенной между горизонтальной прямой, которая отвечает температуре tкр затвердевания, и параболой n-го порядка, которая соответствует распределению температуры в сечении корки для момента τ. Чтобы определить элементарное количество dQакк, надо продифференцировать полученную формулу (6.52). Найденная таким образом величина dQакк будет равна изменению количества теплоты Qакк за время dτ. Это изме-

нение связано с перемещением фронта затвердевания на величину dξ.

Формула в правой части содержит две переменные величины – ξ и t1п.

Чтобы выполнить операцию дифференцирования, необходимо одну из указанных величин выразить через другую. Это можно сделать на основе геометрических соображений.

Действительно, касательная на поверхности отливки к температурной кривой всегда проходит через направляющую точку Н (рис. 6.9). Расстояние от поверхности отливки до направляющей точки известно, оно

λ1

равно α1 . Продолжив касательную до пересечения с горизонталью, ко-

торая соответствует температуре tкр, получим подобные треугольники СDВ и СЕН. Из этих треугольников находят необходимые связи между переменными.

Для определения величины подкасательной СD воспользуемся выражением (6.46). Из рис. 6.9 видно, что угол наклона касательной равен ω. Угол ϕ = 180-ω, следовательно

∂t

)

tgϕ = −

кр

−t

1п

(6.53)

∂y n

Из треугольника DCB находим

tgϕ =	tкр −t1п
tgϕ =	CD .	(6.54)

Из двух последних равенств следует, что

CD =	ξ .	(6.56)
	n

Теперь можно найти связь между величинами ξ и t1п. Из подобных треугольников СDВ и СЕН получается:

BD	=	HE		tкр − t1п = tкр − tc

			или	ξ	ξ	λ .	(6.56)
DC		EC	или	ξ	ξ	λ .	(6.56)
					n +	1
				n		α1
				n		α1

Отсюда имеем необходимую связь

100

tкр −t1п =	tкр −tc
				(6.57)
1 + n		λ1	.
		α ξ
		1

Подставим полученную разность температур в выражение (6.52) для количества аккумулированной теплоты:

Q =

F γ

C (t

−t

)

n +1

кр

λ1 .

(6.58)

акк

1 1

1+ n

α1ξ

Элементарное количество аккумулированной теплоты получается путем дифференцирования:

		1		+ 2n		λ1
1		1		+ 2n		α ξ
1		F1γ1C1 (tкр −tс )				α ξ
dQакк =						1		dξ .	(6.59)
dQакк =	n +1				λ		2	dξ .	(6.59)
				+ n		1
					α ξ
			1		α ξ
						1

Величина dQкр, входящая в уравнение теплового баланса, определяется из выражения

Qкр = F1γ1 ρ1dξ ,

(6.60)

где ρ1 – удельная теплота кристаллизации металла; F1 dξ − объем корки,

затвердевшей за время dτ.

Подставляя найденные значения величин dQ, dQкр, dQакк в уравнение теплового баланса (6.44), находим:

tкр −t1п

1+ 2n

λ1

λ1n

F1dτ =

F1γ1C1

(tкр −tc )

α1ξ

dξ + F1γ1 ρ1dξ .

n +1

+ n

α ξ

(6.61)

Заменив в этом уравнении разность температур tкр – t1п и произведя некоторые преобразования, получим:

101

2ξ

α1

ξ 2

nλ

dξ

а dτ =

dξ +

ξ dξ +

n(n +1)

, (6.62)

Сϑ

nC ϑ

α1

кр

+ nλ

где ϑкр – температура затвердевания, отсчитываемая от температуры tс

окружающей среды, как от нуля, (ϑкр = tкр – tс); а1 – коэффициент температуропроводности затвердевшей корки:

α1 =	λ1		.	(6.63)
	Сγ	1
	1

Полученное дифференциальное уравнение с разделяющимися переменными легко интегрируется, так как оно содержит только хорошо известные табличные интегралы. Имеем

ρ λ

ξ2

аτ =

ξ +

−

С1ϑкр

α1

n +1

α1

2nC1ϑкр

2n(n +1)

n +1

(6.64)

λ2

+C′

+ξ

α1

Постоянная интегрирования С′ находится из следующего условия:

при τ = τ2,

ξ = ξ2.

Подставляя эти значения величин в предыдущее выражение, полу-

чаем

λ2

′

= a1τ2

С ϑ

+ n +1

−

2nC ϑ

+ 2n(n +1) ξ2

+ n +1

α 2

−

ξ2

ln n

+ξ2 .

1 кр

(6.65)

Разделив искомое решение на Х12, а также подставив в него значение величины С′, окончательно будем иметь

	= A1 (δ −δ2 )+ A2 (δ 2 −δ22 )+ A3		1 +		δBi1
Fo − Fo2		ln				n
Fo − Fo2		ln	1 +	δ				,	(6.66)
				δ		2	Bi	,	(6.66)
						2	1
						n
						n

102

где

а1τ

;

Fo2 =

а1τ2

;

X12

A =

;

A =

;

A = −

;

n +1

Bi 2

Bi =

а1

;

L =

ρ1

;

δ =

;

ξ2

;

C ϑ

1 кр

ϑкр

= tкр

−tc .

Формула

(6.66) дает искомую связь между толщиной затвердевшей

корки и временем. Число переменных в этой формуле снижено до минимума путем введения их в состав критериев подобия.

Величины Fo, Fo2, δ, δ2, Bi1 и L представляют собой критерии подобия (безразмерные комбинации физических величин).

Критерий Фурье (Fo) представляет собой безразмерное или относительное время. Критерий Fo2 характеризует время, соответствующее началу третьей стадии охлаждения отливки.

Критерий δ есть относительная или безразмерная толщина корки.

Критерием δ2 определяется начальная безразмерная толщина корки для третьей стадии процесса.

Критерий Био (Bi1), как уже было установлено ранее, характеризует относительную интенсивность теплообмена между телом и окружающей средой. На этом основании критерий Bi1 можно назвать относительным или безразмерным коэффициентом теплообмена.

Критерий L является специфическим для процессов, сопровождающихся фазовыми превращениями. Его можно назвать относительной или безразмерной теплотой кристаллизации.

Решение (6.66) является наиболее общим. Путем правильного выбора показателя n точность этого решения может быть приведена в соответствие с запросами инженерной практики.

103

При расчете свойств отливки важное значение имеет скорость изменения толщины затвердевшей корки во времени (линейная скорость затвердевания), которая определяется по формуле

u =	dξ	.	(6.67)

	dτ

Эта скорость может быть найдена из общего выражения (6.66) посредством его дифференцирования.

Определим в начале безразмерную линейную скорость затвердевания (критерий линейной скорости затвердевания)

U =	dδ	(6.68)
	dFo

путем непосредственного дифференцирования формулы (6.66):

U =	dδ =	1
	dδ =	A1 + 2A2δ +	A3			.	(6.69)
	dFo		A3			.	(6.69)
	dFo		δ +		n
					n
				Bi
				Bi

Как видим, безразмерная линейная скорость затвердевания не зависит от начальных параметров τ2 и ξ2 и весьма существенно изменяется с интенсивностью теплообмена (Bi1).

Связь между U и u находим по соотношению, м/ч

dξ

U =

dδ

a τ

dτ

или

u =

U .

dFo

На основе этого соотношения получаем:

u =

dξ

A1 X1

+ 2A2ξ

A X

1 .

(6.70)

dτ

104

Рассмотрим теперь отдельные частные случаи затвердевания от-

ливки, характеризуемые различной интенсивностью теплообмена.
Большая интенсивность теплообмена (Bi >> 1)
Общая формула (6.66) принимает весьма простой вид:
				Fo – Fo2 = A2 (δ2 - δ22),			(6.71)
			1		1
где	A2	=		L +
	A2	=	2n	L +	n +1
			2n		n +1	.

Коэффициенты А1 и А3 в формуле (6.66) обратились в нуль, так как критерий Bi входит в знаменатель.

Частная формула (6.71) легко может быть преобразована к виду, при котором толщина ξ затвердевшей корки непосредственно выражается через время и другие физические величины

ξ =	2n(n +1) a1	(τ −τ2 )+ξ22	.	(6.72)
	L(n +1)+1

Если ξ2 = 0 (начальная корка отсутствует) и τ2 = 0, то из этого выражения получим

	ξ = R τ ,		(6.73)
где R =	2n(n +1) a1
		.	(6.74)
	L(n +1)+1

Формула (6.73) известна как закон квадратного корня и найдена Ламе, Клайпероном и Стефаном на основе изучения замерзания воды или промерзания влажного грунта. Она справедлива для случая затвердевания отливки в условиях бесконечно большой интенсивности процесса. При этом должны отсутствовать две предыдущие стадии теплообмена

(τ2 = 0 и ξ2 = 0).

Воспользовавшись формулой (6.66), определим безразмерную линейную скорость затвердевания металла. После дифференцирования выражения (6.66) будем иметь

105

U =	dδ	=	1	.	(6.75)
U =	dFo	=	2 A δ	.	(6.75)
			2

Отсюда определим линейную скорость затвердевания

u = dξ	=	a1		=		a1n			,.	(6.76)
		2A	ξ			1
dτ
		2			L +			ξ
							n +1

Эту частную формулу можно получить также из выражения (6.70), если в нем Bi1 = ∞. При этом коэффициенты А1 и А3 обращаются в нуль.

Для частного случая Bi >> 1 легко выразить линейную скорость затвердевания в функции времени. Из формул (6.72) и (6.76) находим

u =

dξ

a1n

dτ

2n (n +

1) a

(τ −τ2 )

+ξ22

(6.77)

L +

n +1

L(n +1)+1

Если начальная корка отсутствует (τ2 = 0 и ξ2 = 0), то

u =

dξ

a1n

(6.78)

dτ

L +

n +1

где R находится из (6.74).

Две последние формулы можно также получить путем непосредственного дифференцирования (6.72) и (6.73).

Малая интенсивность теплообмена (Bi << 1)

Чтобы получить из общего выражения (6.66) частную формулу, справедливую для малой интенсивности теплообмена, разложим натуральный логарифм формулы (6.66) в ряд. Для этого логарифм представим в виде

1 + δBi1 ln n

1 + δ2nBi1

δBi

−

= ln 1

1 +

(6.79)

106

Тогда в соответствии с формулой

ln(1 +U )=U −

U 2

U 3

−

U 4

+...,

(6.80)

которая используется для разложения логарифма в ряд, получим

δBi

δ2

δBi1

δ2

δBi1

δ2

1 +

−

1 −

−

−...

δ2 Bi1

2 Bi1

δ2 Bi1

(6.81)

1 +

Воспользуемся первым слагаемым этого ряда. Кроме того, будем

считать, что при Bi << 1 величина

δ2 Bi1

, входящая в знаменатель пер-

вого слагаемого, пренебрежимо мала по сравнению с единицей (что действительно так, ибо множители δ2 и Bi1 много меньше единицы, а показатель n несколько больше единицы). В результате можно приближенно принять, что

δBi

δ2

1 +

−

δBi

−

2 Bi1

1 +

δ2 Bi1

1 +

(6.82)

Подставив значение логарифма в общую формулу (6.66), после некоторых преобразований получим

Fo − Fo2

(δ −δ2 ).

(6.83)

При выводе (6.83) в правой части оказалось два слагаемых

Fo − Fo2

= L +

(δ −δ2 )+

(δ

−δ2

) .

(6.84)

n +1

107

Из них первое, включающее величину (δ − δ2), имеет в знаменателе критерий Bi, а второе, включающее разность (δ2 − δ22) не содержит его. Поскольку Bi << 1, то первое по абсолютной величине значительно превосходит второе слагаемое, которым возможно пренебречь по сравнению с первым. Так как при Bi<<1 направляющая точка Н (рис. 6.7 … 6.9) стремится в бесконечность, перепад температуры в сечении затвердевшей корки отливки обращается в нуль, и поэтому температурная кривая практически не отличается от горизонтальной прямой. По этой причине в формуле (6.83) не содержится показателя n.

Из выражения (6.83) следует, что толщина затвердевшей корки (при B<<1) пропорциональна времени в первой степени (линейная зависимость).

Критерий линейной скорости затвердевания для относительно малой интенсивности теплообмена определяется путем дифференцирования выражения (6.83)

U =	dδ	=	Bi1
				.	(6.85)
	dFo		L

Линейная скорость затвердевания

u =	dξ	=	a	Bi	=	a1 (tкр − tc )
			1	1			.	(6.86)
	dτ		X1	L
						γ1 ρ1

Как видим, при Bi1 << 1 линейная скорость затвердевания плоской отливки является величиной постоянной (не зависящей ни от толщины затвердевшей корки, ни от времени). Скорость оказывается прямо пропорциональной интенсивности теплообмена (критерию Bi или коэффициенту теплоотдачи α1).

Средняя интенсивность теплообмена (Bi ≈ 1)

Из общего решения уравнения (6.66) можно получить упрощенную формулу применительно к средней интенсивности теплообмена. Для этого надо воспользоваться не одним, а двумя первыми слагаемыми

108

разложения логарифма в ряд. По-прежнему будем считать, что величи-

на

δ2 Bi1

пренебрежимо мала по сравнению с единицей из–за малости

δ2 . Тогда логарифм можно будет представить в виде:

δBi1

1 −

−

1 −

1 +

(6.87)

Подстановка выражения (6.87) в (6.66) дает

Fo − Fo2 =

(δ −δ2 )+

(δ −δ2 )

(δ

−δ2 ).

2n(n +1)

n +1

Полученную формулу можно еще упростить, если принять, что квадрат разности (δ − δ2)2 мало отличается от разности квадратов (δ2 −

δ22) (такое упрощение вполне справедливо при малых значениях δ2):

Fo − Fo2

(δ −δ2 )+

(δ

−δ2

(6.88)

n +1

Критерий линейной скорости затвердевания находится посредством дифференцирования (6.88):

U =	dδ	=				1
			L		1	2	.
	dFo

				+			+ L δ
			Bi1		n
						n +1

Линейная скорость затвердевания вычисляется по формуле

u =

dξ

dτ

+ L ξ

Bi1

n +1

(6.89)

(6.90)

В данном случае u зависит от толщины затвердевшей корки. Чтобы исключить из (6.90) ξ, необходимо решить квадратное уравнение (6.88)

относительно δ. Тогда можно выразить скорость U через время τ. Однако в этом нет особой необходимости.

109

Выбор показателя n. Выбор показателя n может осуществляться различными способами:

−можно найти путем сравнения точного решения задачи (если такое имеется) с приближенным;

−можно найти экспериментально, снимая соответствующую кривую распределения температуры в сечении затвердевшей корки (этот способ дает хорошие результаты и будет использован в дальнейшем);

−можно определить на основе приближенного решения задачи методом конечных разностей;

−можно найти путем гидравлического или электрического моделирования процесса затвердевания отливки.

Для определения величины n применительно к плоской отливке воспользуемся известным решением Стефана, относящимся к случаю промерзания полуограниченного влажного грунта в условиях бесконечно большой интенсивности теплообмена. По Стефану, продвижение фронта промерзания в грунте определяется законом квадратного корня:

ξ = R τ ,

(6.91)

где R – корень трансцендентного уравнения:

λ1 (tкр − t1n )

−4αR2

λ11 (tзал

− t1n )

−4αR1

ρ1γ11

R ,

(6.92)

α1 erf

α11 erf

2 a1

где tкр – температура кристаллизации металла; t1п – температура поверхности отливки; tзал – температура заливаемого металла; λ − коэф-

фициент теплопроводности; α − коэффициент температуропроводности;

ρ − удельная теплота кристаллизации; γ1 − удельный вес.

Индекс «1» означает принадлежность физической величины затвердевшей корке, штрихом вверху обозначены величины, относящиеся к жидкому металлу.

110

Предположим, что начальная температура расплава равна температуре кристаллизации (tзал = tкр). Тогда трансцендентное уравнение (6.92) несколько упрощается (рис. 6.11):

Рис. 6.11. Распределение температуры в сечении промерзшего грунта в моменты τ и τ + dτ (показано пунктиром); начальная

температура грунта равна температуре затвердевания

λ (t

кр

− t

)

ρ γ 1

1 1

R .

exp

−

(6.93)

4a1

a1 erf

В (6.92) и (6.93) использованы следующие общепринятые обозначения:

exp(-u) = e-u;

erf (u) =	2	∫u e−u2 du (функция ошибок Гаусса);
	π
		0

erfc (u) = 1 – erf (u).

Трансцендентные уравнения (6.92) и (6.93) относительно R аналитически решены быть не могут, поэтому прибегнем к графоаналитическим приемам.

111

Обозначим левую часть (6.93) через Х, а правую через У. Имеем

		λ1 (tкр	− t1n )				R2
Х =						−
				R				,
				R	ехр		4a1	,
		α1 erf
		α1 erf		2 a1
				2 a1
Y =	ρ γ 1 π			R .
	1 1
	2
	2

Если теперь задаться вопросом различным значениям коэффициента R и построить кривые X=f(R) и Y=ϕ(R), то точка пересечения этих кривых будет соответствовать искомому значению R, так как именно этому значению отвечает равенство левой и правой частей трансцендентного уравнения (рис. 6.12).

Рис. 6.12. Зависимость величин X и Y от константы затвердевания R для стали

В качестве примера произведем необходимые вычисления для стали, чугуна и алюминия, обладающих различными температурами кристаллизации и соответствующими теплофизическими коэффициентами. Температуру t1п будем считать 20 0С. Значения функции ошибок Гаусса и экспоненты находим в специальных таблицах. Температура затвердевания для сталей и чугунов берется средней между ликвидусом и солидусом (для стали – 1480 0С, для чугуна – 1225 0С). Так, пересечение ли-

112

ний Х и Y на рис. 6.12 соответствует значению коэффициента R = 0,278 м/ч1/2 для стали, для чугуна – 0,305 м/ч1/2, для алюминия – 1,2 м/ч1/2. По вычисленным значениям R определяется показатель степени n, входящий в приближенное значение уравнения (6.66), полученное методом исключения переменных.

Выше было показано, что формула (6.91) может применяться для расчета процесса затвердевания плоской отливки только в том случае, если интенсивность теплообмена бесконечно велика (Bi>>1) и отсутствуют две первые стадии охлаждения (τ2 = 0, ξ2 = 0). При этом коэффициент пропорциональности R определяется из (6.74). По этой формуле, представляющей собой уравнение второй степени относительно n, легко вычислить искомое значение показателя n:

	1			R	2	L		1			R	2	L		R	2	(L	+1)
n = −			−							−				+
	2			2a				4			2a						2a		.	(6.94)
		1					+		1
						1							1				1

Только положительный корень имеет смысл для поставленной задачи. Вычисляем показатель и для рассмотренных сплавов. Критерий L

	ρ			64	= 0,266 ; для чугуна L
для стали имеет значение	1		=
для стали имеет значение	С ϑ		=	0,165(1480 − 20)
1		кр

= 0,332 и для алюминия L = 0,56.

Подставив полученные значения величин в расчетную формулу, найдем: для стали n = 1,33; для чугуна – n = 1,29 и для алюминия n = 1,20.

Как видим, для различных условий затвердевания плоской отливки получатся довольно близкие между собой значения показателя степени n. Наличие известной разницы между величинами n для рассмотренных металлов объясняется неодинаковыми относительными теплофизическими свойствами этих металлов (неодинаковым соотношением между

113

количеством теплоты кристаллизации ρ1 и количеством аккумулированной теплоты С1ϑкр и т. д.).

Таким образом, показатель n найден для случая Bi>>1. Для нахождения показателя n для других условий процесса теплообмена сначала рассмотрим результаты анализа влияния различных факторов на величину n. В общем случае величина n зависит от теплофизических свойств отливки, температурных условий ее охлаждения, интенсивности теплообмена и конфигурации. Рассмотрим этот вопрос подробно применительно к плоской отливке.

Из формулы (6.66) следует, что показатель n должен зависеть главным образом от критериев L, Bi и δ (величина n является безразмерной, поэтому ее также следует рассматривать как критерий подобия). Критерии Fo, Fo2 и δ2 косвенно характеризуют толщину δ затвердевшей корки, поэтому они из рассмотрения выпадают.

Соответствующая критериальная зависимость приобретает вид: n = f (L; Bi; δ).

Анализ (теоретический и экспериментальный) показывает, что характер температурной кривой мало изменяется с толщиной затвердевшей корки. Поэтому можно записать:

n = ϕ(L; Bi).

Остается выяснить влияние критериев L и Bi на величину n и таким образом решить вопрос о выборе показателя n для любых условий теплообмена.

Перепишем критерий L в виде

N =	1	=	С1 (tкр − t1п )
				.	(6.95)
	L
			ρ1

В него вместо температуры tс окружающей среды входит температура t1п поверхности отливки (температуры tс и t1п совпадают только в условиях бесконечно большой интенсивности теплообмена).

114

В нашем распоряжении имеется строгое решение Стефана, полученное для Bi>>1. Воспользовавшись этим решением, найдем зависимость между n и N. С этой целью при определении показателя n будем изменять температуру t1п, входящую в критерий N.

На рис. 6.13 приведены результаты расчета коэффициента затвердевания R для различных температур поверхности плоской отливки из стали. Резкое изменение значения R наблюдается при высоких температурах t1п. По найденному значению R вычисляется вышеизложенным способом показатель n (рис. 6.14). На этом же рисунке изображены аналогичные кривые чугуна и алюминия.

Рис. 6.13. Зависимость «константы» затвердевания R от температуры поверхности плоской стальной отливки

Рис. 6.14. Зависимость показателя n от температуры поверхности плоской стальной (кривая 1), чугунной (кривая 2) и алюминиевой

(кривая 3) отливок

115

Все кривые вычислены для значения Bi>>1. Следовательно, для этих кривых должно быть справедливо соотношение n = ψ(N). Из этого уравнения вытекает, что если изобразить полученные кривые на координатной плоскости n – N, то все они должны слиться в одну общую кривую (рис. 6.15). Как видно, все точки, относящиеся к различным металлам, хорошо укладываются на одну кривую. Это значит, что предыдущие соотношения n = ϕ(L; Bi) и n=ψ(N) являются совершенно правильными.

Рис. 6.15. Обобщенная расчетная кривая, связывающая показатель n с критерием N: 1 – железо; 2 – сталь; 3 – чугун; 4 – медь;

5 – алюминий; 6 - цинк

Кривая, изображенная на рис. 6.15, может служить основой для выбора показателя n применительно к различным условиям затвердевания металла. Однако необходимо иметь в виду, что эта кривая получена для постоянного значения Bi = ∞. Из кривых на рис. 6.15 можно сделать следующие выводы:

−большому перепаду δ1t = tкр – t1п в сечении отливки соответствуют более высокие показатели n;

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.02.2016181.83 Кб65Таблицы математической статистики.pdf
#
16.02.201635.33 Кб253Тактика ведения боя пулеметчика.doc
#
16.02.201617.03 Mб153ТЕКСТ.doc
#
16.02.2016575.49 Кб62Теор и практ антуправления.doc
#
16.02.20162.28 Mб462Теория литейных процессов том1.pdf
#
16.02.20162.4 Mб355Теория литейных процессов том2.pdf
#
30.08.2019490.5 Кб91Теория организации. Шпаргалки.doc
#
09.11.201813.83 Mб87Теория принятия решений (дополнительные главы.doc
#
22.04.2019419.84 Кб36Теормех УМК 2010 Задания на контр. работы.doc
#
22.04.20191.94 Mб57Теормех УМК 2010 Кинематика.doc
#
22.04.20191.08 Mб44Теормех УМК 2010 Статика.doc