Типовой расчет ТОЭ СЗГТУ

Задача 1.

1. Изобразим электрическую схему в соответствии с заданным вариантом:

1. Определим токи во всех резистивных элементах:

Выберем произвольно в ветвях положительное направление токов и промаркируем их:

Преобразуем поэтапно схему к одноконтурной:

Определим значение тока I₂:

Определим падение напряжения на параллельном участке цепи:

Определим значение тока I₁:

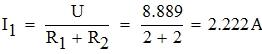
Определим значение тока I₃:

2. Проверим полученные результаты по законам Кирхгофа:

по 1-му закону Кирхгофа:

Задача 2.

1. Изобразим электрическую схему в соответствии с заданным вариантом:

1. Заменим исходную схему эквивалентной.

2. Для определения Ег проведем опыт холостого хода.

По второму закону Кирхгофа.

По второму закону Кирхгофа.

3. Для определения Rг проведем опыт короткого замыкания.

4. Определим ток в ветви 1-2.

Задача 3.

1. Изобразим электрическую схему в соответствии с заданным вариантом:

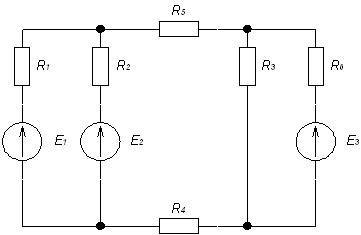
1. Произвольно зададимся направлением токов в ветвях.

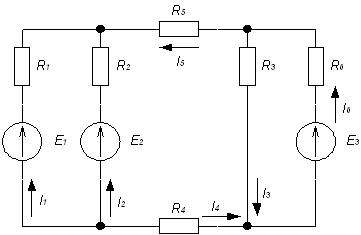
2. Пронумеруем узлы и запишем уравнения по I закону Кирхгофа.

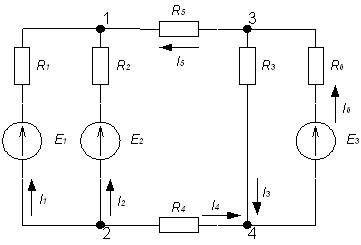
3. Определим независимые контура и зададимся направлением их обхода.

4. Запишем уравнения по II закону Кирхгофа.

Составим систему уравнений по методу контурных токов.

Выражения для сопротивлений контуров имеют вид:

Выражения для сопротивлений связи между контурами имеют вид:

Выражения для контурных ЭДС имеют вид:

Система уравнений, составленная по методу контурных токов в матричном виде имеет вид:

Решив систему уравнений, найдем значения контурных токов:

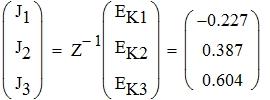
Определим значение токов ветвей:

Составим систему уравнений по методу узловых потенциалов (потенциал узла №4 будем считать равным 0В).

Выражения для собственных проводимостей узлов имеют вид:

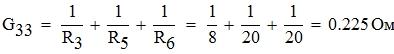
Выражения для взаимных проводимостей узлов имеют вид:

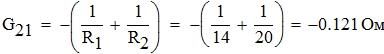
Выражения для узловых токов имеют вид:

Система уравнений, составленная по методу узловых потенциалов в матричном виде имеет вид:

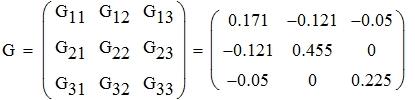
Решив систему уравнений, найдем значения узловых потенциалов:

Определим значение токов ветвей:

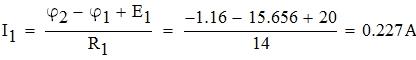
Задача 4.

1. Изобразим электрическую схему в соответствии с заданным вариантом:

1. Определим действующее и мгновенное значение тока на входе I_ВХ комплексным (символическим) методом.

Определим реактивные сопротивления элементов L и C.

Определим комплексные сопротивления ветвей.

Определим комплексное входное сопротивление цепи.

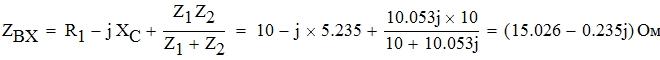
Определим действующее значение тока на входе I_ВХ

Определим мгновенное значение тока на входе I_ВХ

2. Определим как измениться ток цепи, если в ней произвести замены:

- входное синусоидальное напряжение на постоянное напряжение U₀;

Сопротивления ветвей будут чисто активными, причем ветвь с C будет эквивалентна разрыву в цепи.

Входное сопротивление ветви будет равно бесконечности.

Входной ток будет нулевым.

Мгновенное значение входного тока будет равно его действующему значению.

- реактивные элементы L и C на резистивные элементы R₃ и R₄. При этом зададимся условием U=U₀, X_L=R₃, X_C=R₄.

Сопротивления ветвей будут чисто активными.

Входное сопротивление ветви будет чисто активным.

Входной ток также будет чисто активным.

Мгновенное значение входного тока будет равно его действующему значению.

10