
Задача 1
Напряжение
постоянного тока измеряется двумя
вольтметрами – класса точности 4,0
(используется предел измерений
 )
и класса
точности
)
и класса
точности
 (используется предел измерений
(используется предел измерений
 ).
).
Показания
вольтметров составляют соответственно
 и
и

Определить, какой вольтметр предпочтительнее применять для обеспечения большей точности измерений. Указать пределы, в которых находится измеряемое напряжение.
Влиянием входного сопротивления вольтметра пренебречь.
Решение
1. Значение абсолютной погрешности для первого вольтметра вычисляется по следующей формуле:
|
|
(1.1) |
где
 приведенная погрешность измерения,
равная классу точности прибора;
приведенная погрешность измерения,
равная классу точности прибора;
 выбранный
предел измерения прибора.
выбранный
предел измерения прибора.
Тогда значение абсолютной погрешности будет равно:
|
|
(1.2) |
Относительная погрешность будет равна:
|
|
(1.3) |
2. Значение относительной погрешности для второго вольтметра будет равно:
|
|
(1.4) |
|
|
|
Тогда значение абсолютной погрешности будет равно:
|
|
|
где с, d – положительные числа, не зависящие от X;
 стандартный
предел измерения.
стандартный
предел измерения.
Вывод:
результат, измеренный с помощью второго
вольтметра, получен с большей точностью,
т.к.
 .
Истинное значение напряжения для первого
вольтметра лежит в пределах [94; 106], для
второго вольтметра - [97,5; 108,5]. [1]
.
Истинное значение напряжения для первого
вольтметра лежит в пределах [94; 106], для
второго вольтметра - [97,5; 108,5]. [1]
Задача 2
Постоянный ток измеряется миллиамперметром, имеющим следующие метрологические характеристики:
1.
Класс точности:
 .
.
2.
Внутреннее активное сопротивление:
 .
.
За
показание миллиамперметра принять
расчетное значение тока с учетом
 .
Миллиамперметр имеет пределы измерений:
1; 2; 5; 10; 20 мА.
.
Миллиамперметр имеет пределы измерений:
1; 2; 5; 10; 20 мА.
Указать
пределы, в которых находится измеряемый
ток, если на входе цепи действует
напряжение
 ,
а сопротивление нагрузки равно
,
а сопротивление нагрузки равно
 .
.
Решение
1. Рассчитаем показание миллиамперметра:
|
|
(2.1) |
2. Рассчитаем детерминированную поправку к показанием миллиамперметра:
|
|
(2.2) |
3. Рассчитаем значение абсолютной погрешности миллиамперметра, выбрав предел измерения 5 мА:
|
|
(2.3) |
|
|
(2.4) |
где
 - приведённая погрешность (класс точность
прибора);
- приведённая погрешность (класс точность
прибора);
 -
абсолютная погрешность.
-
абсолютная погрешность.
4. Измеряемый ток находится в пределах:
|
|
(2.5) |
|
|
|
Ответ:
 мА.
[1]
мА.
[1]
Задача 3
Определить пределы, в которых находится активная мощность, выделяемая в нагрузке цепи переменного тока промышленной частоты, измеряемая электромеханическим ваттметром электродинамической системы.
Метрологические характеристики ваттметра:
1.
Класс точности ваттметра:
 .
.
2.
Сопротивление последовательной обмотки
ваттметра:
 .
.
3.
Номинальный ток параллельной обмотки
ваттметра:
 .
.
Напряжение
сети
 ,
ток сети
,
ток сети
 ,
угол сдвига фазы между током и напряжением
,
угол сдвига фазы между током и напряжением
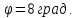
Ваттметр имеет пределы измерений 20; 40; 60 Вт.
Решение
1. Рассчитаем показание ваттметра:
|
|
(3.1) |
2. Рассчитаем детерминированную поправку к показанием ваттметра:
|
|
(3.2) |
4. Рассчитаем значение абсолютной погрешности ваттметра:
|
|
(3.3) |
|
|
(3.4) |
где
 - приведённая погрешность (класс точность
прибора);
- приведённая погрешность (класс точность
прибора);
 -
абсолютная погрешность;
-
абсолютная погрешность;
 – выбранный
предел измерения.
– выбранный
предел измерения.
5. Измеряемый ток находится в пределах:
|
|
(3.5) |
|
|
|
Ответ:
 Вт.
[1]
Вт.
[1]
Задача 4
Для измерения толщины бумажной ленты применен емкостной принцип преобразования.
Чувствительность элемент имеет размеры:
-
площадь пластин конденсатора
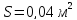 ;
;
-
зазор между пластинами
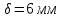 .
.
Рассчитать
и построить функцию преобразования
емкостного преобразователя. Определить
по этой характеристике пределы изменений
емкости преобразователя, если толщина
ленты
 ,
протягиваемой между пластинами,
изменяется от
,
протягиваемой между пластинами,
изменяется от
 до
до
 .
.
Диэлектрическая
постоянная воздуха
 ,
диэлектрическая постоянная бумаги
,
диэлектрическая постоянная бумаги
 .
.
Решение
1. Функция преобразования емкостного преобразователя данного типа определяется аналитической зависимостью:
|
|
(4.1) |
|
|
|
где C – емкость чувствительного элемента.
Зададим функцию преобразования таблично.
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
|
61,0 |
61,6 |
62,1 |
62,7 |
63,2 |
63,8 |
Зададим функцию преобразования графически.

Рисунок 1 – Функция преобразования емкостного преобразователя
Ответ: Пределы изменений ёмкости преобразователя [61,0; 63,8]. [1]
Задача 5
Для измерения амплитудного значения, периода и частоты следования сигнала синусоидальной формы использовался электронно-лучевой осциллограф, причем были выбраны следующие положения органов управления:
-
коэффициент отклонения
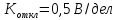 ;
;
-
коэффициент развертки
 .
.
Отклонения
луча на экране осциллографа, соответствующие
измеряемым параметрам: по вертикали
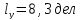 ,
по горизонтали
,
по горизонтали
 ,
а также относительная погрешность
результата измерений напряжения и
времени
,
а также относительная погрешность
результата измерений напряжения и
времени
 .
.
Определить пределы, в которых находятся амплитуда, период и частота следования сигнала.
Решение
1. Определим значение амплитуды сигнала синусоидальной формы:
|
|
(5.1) |
2. Определим значение периода сигнала синусоидальной формы:
|
|
(5.2) |
3. Определим значение частоты сигнала синусоидальной формы:
|
|
(5.3) |
4. Определим значения абсолютных погрешностей для измеренных и рассчитанных значений:
|
|
(5.4) |
|
|
(5.5) |
|
|
|
|
|
|
5. Измеренные значения находятся в пределах:
|
|
(5.6) |
|
|
|
|
|
Ответ:
 В;
В;
 мс;
мс;
 кГц.
[1]
кГц.
[1]
Задача 6
Необходимо измерить частоту или период сигнала переменного тока синусоидальной формы при помощи типового цифрового мультиметра, основные технические характеристики которого приведены в таблице 3.
Показания мультиметра:
 ;
;
 .
.
Определить
для значения частоты
 ,
какой параметр (частоту или период)
рационально измерить, исходя из требований
точности измерений.
,
какой параметр (частоту или период)
рационально измерить, исходя из требований
точности измерений.
Таблица 1

Решение
1.
Рассчитаем относительную погрешность
результата измерения частоты, выбрав
время счета
 мс:
мс:
|
|
(6.1) |
2.
Рассчитаем относительную погрешность
результата измерения периода, выбрав
цену метки времени
 мкс и множитель периода
мкс и множитель периода
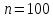 :
:
|
|
(6.2) |
Вывод:
относительная
погрешность измерения частоты гораздо
меньше, чем относительная погрешность
измерения периода. При дальнейшем
анализе видно, что погрешности измерения
частоты и периода будут равны при частоте
сигнала 1 кГц ( ,
,
 ).
При частоте сигнала меньше 1 кГц
погрешность измерения периода будет
меньше, чем погрешность измерения
частоты, а при частоте сигнала больше
1 кГц – наоборот: погрешность измерения
частоты будет меньше, чем погрешность
измерения периода.
).
При частоте сигнала меньше 1 кГц
погрешность измерения периода будет
меньше, чем погрешность измерения
частоты, а при частоте сигнала больше
1 кГц – наоборот: погрешность измерения
частоты будет меньше, чем погрешность
измерения периода.

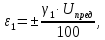


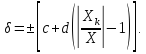






 мА,
мА, мА.
мА.



 Вт,
Вт,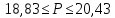 Вт.
Вт.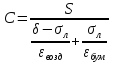
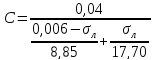


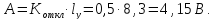






 В;
В; мс;
мс; Гц.
Гц.
