Математика(шифр 03)

№1 Решить дифференциальное уравнение первого порядка

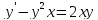
Решение:

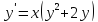
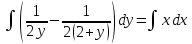
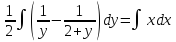
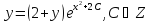
Ответ:

№2 Решить дифференциальное уравнение методом понижения порядка

Решение:

Сделаем замену

Подставим в исходное уравнение

Получили уравнение с разделяющимися переменными

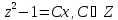
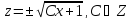
Ответ:

№3 Найти общее решение дифференциального уравнения второго порядка

Решение: 1)Выпишем характеристическое уравнение данного линейного уравнения:

Корнем данного уравнения является: .

Тогда:

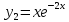
Общее решение однородного уравнения:

2)Ищем частное решение уравнения по виду правой части: . Частное решение ищем в виде:

.

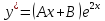
Подставим и и 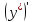в исходное уравнение:

Итак, частное решение:

Общее решение данного неоднородного уравнения:

Ответ:

№4 4 Найти область сходимости степенного ряда и исследовать сходимость на концах интервала сходимости

Решение: Составим положительный ряд из абсолютных величин членов исходного ряда:

С общим членом . По признаку Даламбера полученный ряд сходится, если предел существует и удовлетворяет условию ,

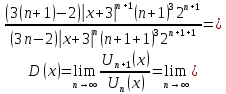
Отсюда получим , что равносильно . Получили интервал сходимости .

Изучим поведение ряда на концах полученного интервала. На правом конце (x=-1)

получаем числовой ряд .

– сходится как обобщенный гармонический ряд с показателем степени p = 2, тогда исходный ряд также сходится.

На левом конце интервала (x=-5) получается ряд: .

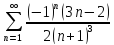Применим признак Лейбница. Так как

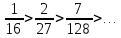, то первое условие признака Лейбница выполнено. Далее, т.к.

, то . Теперь выясним, сходится ли этот ряд абсолютно. Для этого исследуем сходимость ряда, составленного из абсолютных величин.

– сходится как обобщенный гармонический ряд с показателем степени p = 2. Значит исходный ряд сходится абсолютно.

Ответ: .

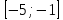№5 Разложить функцию в ряд Маклорена , определить область сходимости ряда.

Решение:

Воспользуемся тригонометрическим разложением

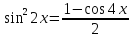
Воспользуемся известным разложением:

В разложении вместо x подставляем 4

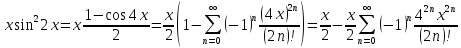
Область сходимости: .

№6 Построить область интегрирования и изменить порядок интегрирования.

Решение: Переменная в области D изменяется в промежутке: , т.е. область D заключена между вертикальными прямыми: . Пределы интегрирования по переменной показывают, что снизу область D ограничена линией , а сверху - линией .

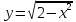D₂

D₁

Теперь поменяем порядок интегрирования, приняв за внешнюю переменную не , а . Разобьем область D горизонтальной прямой на области D₁ и D₂ . Тогда

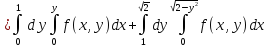
№7 Найти массу пластины, заданной неравенствами: 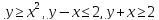если ее плотность .

Решение:

D

D₁

D₂

Массу M, рассматриваемой пластины будем находить по формуле:

Разобьем область D горизонтальной прямой на области D₁ и D₂ . Тогда

(

№8 Вычислить криволинейный интеграл по кривой

где отрезок , где

Решение:

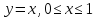Поскольку отрезок задается уравнением , то получим