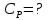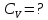контрольная работа 1 Физика вариант 2
.docxАвтономная некоммерческая организация высшего профессионального образования
«СЕВЕРО-ЗАПАДНЫЙ ОТКРЫТЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Факультет_Энергетики и машиностроения __
ФИЗИКА
Контрольная работа №1
Вариант 2
Ф.И.О. студента__Громов Алексей Андреевич
Направление подготовки:__Электроэнергетика и электротехника________ Шифр____140282
Дата выполнения работы___23.01.2015__
Проверил преподаватель__________________
Тихвин
2015 г.
103. Прямолинейное движение двух материальных точек описывается уравнениям х1=A1+ B1t2+ C1t3 и х2 = A2+ B2t2+ C2t3 , где A1 =4 м/с; B1=8 м/с2; C1=-16 м/с3; A2=2 м/с; B2=-4 м/с2; C2=1 м/с3.
|
Дано: х1=A1+ B1t2+ C1t3 х2 = A2+ B2t2+ C2t3 A1 =4 м/с; B1=8 м/с2; C1=-16 м/с3 A2=2 м/с; B2=-4 м/с2; C2=1 м/с3 |
Решение: Так как требуется найти скорость и ускорение в момент времени, то нужно определить мгновенные значения скоростей и ускорений. Мгновенная скорость v есть первая производная ее координаты по времени. |
|
a1=? a2=? |
|
|
Получим
выражения для
Определим
момент времени , в который
Откуда
Подставляя числовые значения в формулу, получим:
Ускорение точек найдем, взяв производную от скорости по времени:
Из выражений видно, что движение обеих точек происходит с постоянным ускорением:
Ответ:
t=0,3с;
a1=-32 |
|
113. Из орудия вылетает снаряд массой 10 кг со скоростью 600 м/с. Определить среднюю силу давления пороховых газов, если снаряд движется внутри ствола орудия в течение 0,005 с.
|
Дано:
|
Решение: Определим среднюю силу давления пороховых газов с помощью второго закона Ньютона для импульсов:
|
|
|
|
|
|
|
Подставляя числовые значения в формулу, получим:
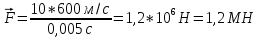
Ответ: 1,2 МН
123. С железнодорожной платформы, движущейся прямолинейно со скоростью 2,5 м/с, в направлении, противоположном ее движению, выстрелили из пушки. Масса платформы с пушкой 20 т, масса снаряда 20 кг, его начальная скорость 600 м/с. Определить скорость платформы после выстрела.
|
Дано:
|
Решение:
|
|
|
|
|
Согласно закону сохранения импульса: импульс системы остается постоянным при любых взаимодействиях внутри, или импульс системы снаряд – орудие с платформой до выстрела равен импульсу этой системы после выстрела: |
|
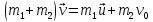
Проекция на ось
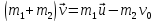
Исходя из формул следует, что
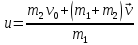
Подставим в полученную формулу числовые значения и получим:
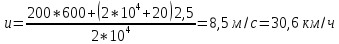
Ответ:
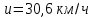
133. Молотком массой 1 кг забивают в стену гвоздь массой 75 г. Определить КПД удара.
|
Дано:
|
Решение: Коэффициент полезного действия равен отношению кинетической энергии одного тела к кинетической энергии другого. |
|
|
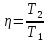
Кинетическая энергия одного тела:
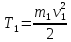
Кинетическая энергия второго тела:
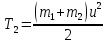
По закону сохранения импульса:
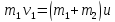
Откуда

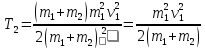
Подставим
найденное значение
 в формулу по нахождению КПД:
в формулу по нахождению КПД:
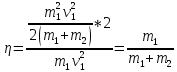
Подставим числовые выражения в полученную формулу:
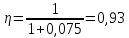
Ответ:
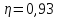
143. Тонкий стержень длиной 50 см и массой 400 г вращается с угловым ускорением 3 рад/с2 вокруг оси, проходящей через его середину, перпендикулярно длине стержня. Определить вращающий момент.
|
Дано:
|
Решение: Вращающий момент равен произведению момента инерции твердого тела на угловое ускорение.
|
|
|
Момент инерции для стержня
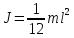
Отсюда

Подставив числовые значения в формулу, получим:
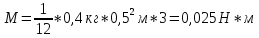
Ответ:
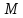 =
0,025
=
0,025
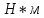
153. Определить число молей и число молекул газа, содержащегося в колбе емкостью 10 л, если температура газа равна 17 0С, а давление 50 кПа.
|
Дано:
|
Решение: Согласно уравнению Менделеева-Клапейрона
|
|
|
Тогда число молей газа
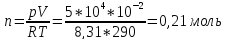
Число молекул газа равно произведению количества вещества на постоянную Авогадро:
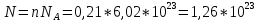
Ответ: n=0,21моль, N=1,26*1023
163. 1 кг двухатомного газа находится под давлением 80 кПа и имеет плотность 4 кг/м3. Найти полную энергию теплового движения молекул в этих условиях.
|
Дано:
|
Решение: Энергия теплового движения двухатомного газа определяется выражением:
|
|
|
Согласно уравнению Менделеева-Клапейрона
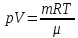
Тогда энергию теплового движения двухатомного газа можно записать в виде
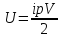
где
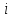 =5 – число степеней свободы двухатомного
газа.
=5 – число степеней свободы двухатомного
газа.
Объем, занимаемый газом равен отношению массы газа к его плотности
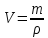
Подставим уравнение объема в уравнение энергии теплового движения:
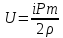
Подставим в выражение численные значения и найдем энергии. Теплового движения:
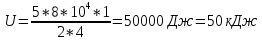
Ответ:
 =50кДж.
=50кДж.
173. Вычислить удельные теплоемкости газа при постоянном давлении и при постоянном объеме, зная, что его молярная масса равна 44·10-3 кг/моль, а показатель адиабаты равен 1,33.
|
Дано:
|
Решение: Показатель адиабаты равен отношению молярной теплоемкости при постоянном давлении к молярной теплоемкости при постоянном объеме: |
|
|
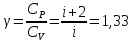
Откуда
число степеней свободы
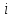 = 6
= 6
Найдем молярную теплоемкость газа при постоянном давлении:
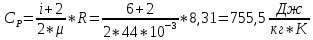
Найдем молярную теплоемкость газа при постоянном объеме:
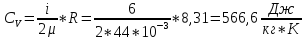
Ответ:
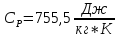
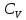 =
=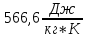

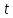 =?
(при v1=v2)
=?
(при v1=v2)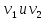 :
: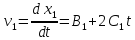
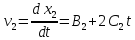
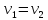 ,
для чего приравняем правые части
выражений:
,
для чего приравняем правые части
выражений: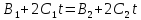
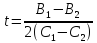


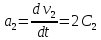
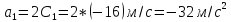
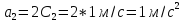
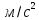 ,
a2=1
,
a2=1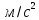
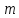 =10кг
=10кг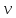 =600
м/с
=600
м/с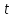 =0,005
с
=0,005
с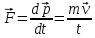
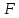 =?
=?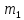 =
20т =2*104кг
=
20т =2*104кг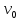 =
600 м/с
=
600 м/с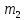 =
20 кг
=
20 кг =2,5
м/с
=2,5
м/с
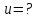
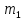 =
1кг
=
1кг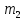 =
75г=0,075 кг
=
75г=0,075 кг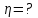
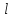 =
50 см=0,5м
=
50 см=0,5м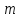 =
400г=0,4 кг
=
400г=0,4 кг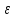 =3
рад/с2
=3
рад/с2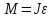
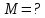
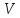 =
10л=10-2 м3
=
10л=10-2 м3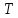 =
170С=290К
=
170С=290К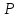 =50кПа=5*104Па
=50кПа=5*104Па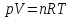
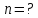
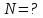
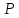 =
80кПа=8*104Па
=
80кПа=8*104Па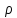 =
4кг/м3
=
4кг/м3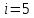
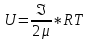
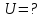
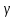 =
1,33
=
1,33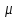 =
44*10-3кг/моль
=
44*10-3кг/моль