
- •Федеральное агентство по образованию
- •Предисловие
- •Введение
- •Глава 1. Линейные пространства § 1. Введение
- •§ 2. Определение линейного пространства
- •I и II операции называются соответственно сложением и умножением на число и удовлетворяют следующим восьми условиям:
- •Примеры конкретных линейных пространств
- •§ 4. Линейная зависимость
- •§ 5. Базис и координаты
- •§ 6. Размерность
- •§ 7. Подпространства
- •Глава 2. Евклидовы пространства § 1. Введение
- •§ 2. Определение евклидова пространства
- •§ 3. Длина вектора
- •§ 4. Неравенство Коши-Буняковского
- •§ 5. Неравенство треугольника
- •§ 6. Угол между векторами
- •§ 7. Ортонормированный базис
- •Глава 3. Линейные операторы § 1. Определение линейного оператора
- •§ 2. Примеры линейных операторов
- •Примеры линейных операторов
- •§ 3. Действия над линейными операторами
- •Глава 4. Преобразование координат § 1. Замена базиса
- •§ 2. Ортогональные преобразования
- •§ 3. Матрица оператора при замене базиса
- •Глава 5. Несовместные системы линейных уравнений и метод наименьших квадратов § 1. Задача о проекции вектора и перпендикуляре к нему
- •§ 2. Несовместные системы линейных уравнений
- •§ 3. Метод наименьших квадратов
- •Глава 6. Собственные векторы и собственные числа § 1. Определение собственных векторов и собственных чисел
- •§ 2. Вычисление собственных векторов и собственных чисел в конечномерном пространстве
- •§ 3. Собственные векторы симметричных операторов
- •Глава 7. Квадратичные формы и их приведение к каноническому виду § 1. Приведение квадратичной формы к каноническому виду
- •§ 2. Приведение двух квадратичных форм к каноническому виду
- •§ 3. Малые колебания механических систем
- •Глава 8. Элементы теории метрических пространств § 1. Определение метрического пространства
- •§ 2. Сходимость. Полные метрические пространства
- •§ 3. Принцип сжимающих отображений
- •Библиографический список
- •191186, Санкт-Петербург, ул. Миллионная, 5
§ 2. Сходимость. Полные метрические пространства
Введем некоторые понятия теории метрических пространств, которые будут использованы в дальнейшем.
Пусть
![]() означает некоторую точку метрического
пространства
означает некоторую точку метрического
пространства![]() ,
а
,
а![]() – положительное число.
– положительное число.
Определение.
Совокупность
точек
![]() пространства
пространства![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]()
называется
замкнутым
шаром и
обозначается символом
![]() .
.
Точка
![]() называется центром этого шара, а число
называется центром этого шара, а число![]() – радиусом шара.
– радиусом шара.
Определение.
Совокупность
точек
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
,
называется
открытым
шаром и
обозначается символом
![]() .
.
Открытый шар
радиуса
![]() с центром в точке
с центром в точке![]() называют
называют![]() –окрестностью
точки
–окрестностью
точки
![]() и обозначают символом
и обозначают символом![]() .
.
Определение.
Точка
![]() называетсяточкой
прикосновения множества
называетсяточкой
прикосновения множества
![]() ,
если любая ее окрестность содержит хотя
бы одну точку из
,
если любая ее окрестность содержит хотя
бы одну точку из![]() .
.
Совокупность всех
точек прикосновения множества
![]() называетсязамыканием
этого множества
и обозначается символом
называетсязамыканием
этого множества
и обозначается символом
![]() .
.
Определение.
Точка
![]() называетсяпредельной
точкой множества
называетсяпредельной
точкой множества
![]() ,
если любая ее окрестность содержит
бесконечно много точек из
,
если любая ее окрестность содержит
бесконечно много точек из![]() .
.
Определение.
Точка
![]() ,
принадлежащая
,
принадлежащая![]() называетсяизолированной
точкой
этого множества, если в достаточно малой
ее окрестности
называетсяизолированной
точкой
этого множества, если в достаточно малой
ее окрестности
![]() нет точек из
нет точек из![]() ,
отличных от
,
отличных от![]() .
.
Пусть
![]() – последовательность точек в метрическом
пространстве
– последовательность точек в метрическом
пространстве![]() .
.
Определение.
Последовательность
![]() сходится к точке
сходится к точке![]() ,
если
,
если
 .
.
Следующая теорема устанавливает связь между понятиями предела и точкой прикосновения множества.
Теорема.
Для того чтобы точка
![]() была точкой прикосновения множества
была точкой прикосновения множества![]() ,
необходимо и достаточно, чтобы существовала
последовательность
,
необходимо и достаточно, чтобы существовала
последовательность![]() точек из
точек из![]() ,
сходящаяся к
,
сходящаяся к![]() .
.
Пусть в метрическом
пространстве
![]() имеется два множества
имеется два множества![]() и
и![]() .
.
Определение.
Множество
![]() называется плотным в множестве
называется плотным в множестве![]() ,
если
,
если![]() .
В частности, множество
.
В частности, множество![]() называется всюду плотным (в пространстве
называется всюду плотным (в пространстве![]() ),
если его замыкание
),
если его замыкание![]() совпадает со всем пространством
совпадает со всем пространством![]() .
.
Например, множество рациональных чисел всюду плотно на числовой прямой.
Пространства, в которых имеется счетные всюду плотные множества, называют сепарательными.
Определение.
Множество
![]() называетсязамкнутым,
если оно содержит все свои предельные
точки или, что то же самое, если оно
совпадает со своим замыканием:
называетсязамкнутым,
если оно содержит все свои предельные
точки или, что то же самое, если оно
совпадает со своим замыканием:
![]() .
.
Определение.
Последовательность
![]() точек метрического пространства
точек метрического пространства![]() называетсяфундаментальной,
если для любого
называетсяфундаментальной,
если для любого
![]() существует такое число
существует такое число![]() ,
что для всех
,
что для всех![]() и
и![]() выполняется неравенство
выполняется неравенство![]() .
.
Нетрудно заметить, что всякая сходящаяся последовательность является фундаментальной. Однако обратное утверждение верно не во всяком метрическом пространстве.
Определение.
Если в
метрическом пространстве
![]() любая фундаментальная последовательность
сходится, то это пространство называетсяполным.
любая фундаментальная последовательность
сходится, то это пространство называетсяполным.
Например, евклидовы
пространства
![]() ,
,![]() ,
а также пространство
,
а также пространство![]() являются полными.
являются полными.
§ 3. Принцип сжимающих отображений
Вопрос о существовании и единственности решений алгебраических, трансцендентных, дифференциальных и других типов уравнений можно сформулировать в виде вопроса о существовании и единственности неподвижной точки при некотором отображении соответствующего метрического пространства в себя. Одним из критериев существования и единственности неподвижной точки при такого рода отображениях является так называемый принцип сжимающих отображений.
Отображение
![]() метрического пространства
метрического пространства
![]() в себя называется сжимающим
отображением,
если существует такое число
в себя называется сжимающим
отображением,
если существует такое число
![]() ,
что для любых двух точек
,
что для любых двух точек![]() и
и![]() пространства
пространства
![]() выполняется неравенство
выполняется неравенство
![]() .
.
Точка
![]() называетсянеподвижной
точкой отображения
называетсянеподвижной
точкой отображения
![]() ,
если выполняется равенство
,
если выполняется равенство
![]() .
.
Можно показать, что имеет место следующее утверждение.
Теорема (Принцип
сжимающих отображений).
Всякое сжимающее отображение, определенное
в полном метрическом пространстве
![]() ,
имеет одну и только одну неподвижную
точку.
,
имеет одну и только одну неподвижную
точку.
Принцип сжимающих отображений можно использовать для доказательства существования и единственности решений для уравнений различных типов. Следует отметить, что принцип сжимающих отображений позволяет не только доказать существование и единственность решения, но и дает метод нахождения приближенного решения. Этот метод называют методом итераций или методом последовательных приближений.
Рассмотрим применение этого метода к отысканию приближенного решения уравнения
![]() ,
(8.1)
,
(8.1)
где функция
![]() определена на промежутке
определена на промежутке![]() и удовлетворяет условию Липшица
и удовлетворяет условию Липшица
![]() ,
(8.2)
,
(8.2)
с константой
![]() и отображает промежуток
и отображает промежуток![]() в себя.
в себя.
В этом случае
![]() есть сжимающее отображение и, согласно
сформулированной выше теореме
последовательность чисел
есть сжимающее отображение и, согласно
сформулированной выше теореме
последовательность чисел
![]() ,
,
![]() ,
,![]() ,…,
,…,![]() …
…
сходится к единственному корню уравнения (8.1).
Если функция
![]() имеет на промежутке
имеет на промежутке![]() производную
производную![]() и при этом выполняется неравенство
и при этом выполняется неравенство
![]() ,
(8.3)
,
(8.3)
где
![]() – некоторая постоянная, то легко видеть,
что условие сжатости (8.2) выполнено.
– некоторая постоянная, то легко видеть,
что условие сжатости (8.2) выполнено.
Рассмотрим примеры.
Пример 1.
На промежутке
![]() найти действительный корень уравнения
найти действительный корень уравнения
![]() .
.
Записав данное уравнение в виде (8.1), получим
![]() .
.
Легко проверяется,
что производная
![]() на промежутке
на промежутке![]() принимает только положительные значения
и удовлетворяет условию (8.2).
принимает только положительные значения
и удовлетворяет условию (8.2).
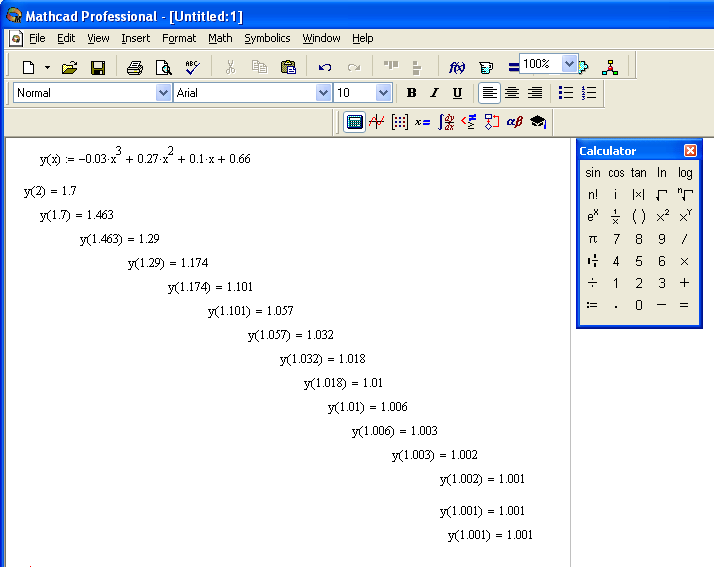
Используя метод
итераций и положив в первом шаге
![]() ,получим с
помощью Mathcad
Professional
,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
,получим с
помощью Mathcad
Professional
,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
Пример 2.
На промежутке
![]() найти действительный корень уравнения
найти действительный корень уравнения
![]() .
.
Как и в предыдущем примере запишем данное уравнение в виде
![]() .
.
В этом примере
производная
![]() на промежутке
на промежутке![]() принимает только отрицательные значения,
но условие (8.2) по прежнему выполняется.
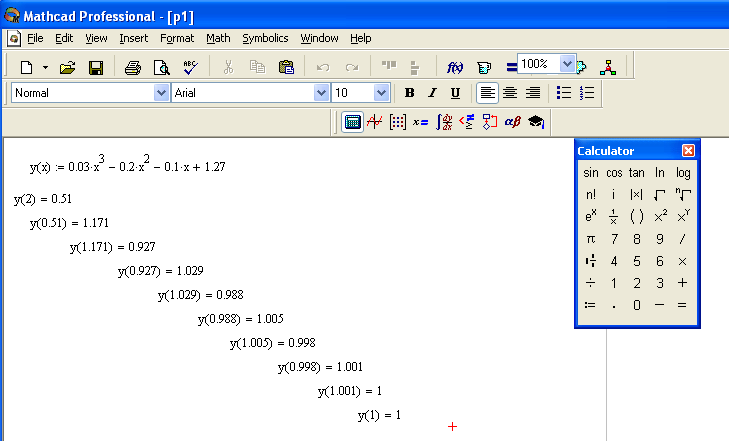
Используя метод итераций и положив
вначале
принимает только отрицательные значения,
но условие (8.2) по прежнему выполняется.
Используя метод итераций и положив
вначале![]() будем производить вычисления с помощьюMathcad
Professional.
будем производить вычисления с помощьюMathcad
Professional.
Геометрически
метод итераций можно пояснить следующим
образом. Построим на плоскости
![]() графики функций
графики функций![]() и
и![]() .
Каждый вещественный корень
.
Каждый вещественный корень![]() уравнения (8.1) является абсциссой точки
пересечения кривой
уравнения (8.1) является абсциссой точки
пересечения кривой![]() с прямой
с прямой![]() (рис.3).
(рис.3).

Рис.3
Отправляясь от
некоторой точки
![]() ,
построим ломаную линию
,
построим ломаную линию![]() («Лестница»), звенья которой попеременно
параллельны оси
(«Лестница»), звенья которой попеременно
параллельны оси![]() и оси
и оси![]() ,
так что вершины
,
так что вершины![]() лежат на кривой
лежат на кривой![]() ,
а вершины
,
а вершины![]() на прямой
на прямой![]() .
Общие абсциссы точек
.
Общие абсциссы точек![]() и
и![]() ,
,![]() и
и![]() ,
,![]() и
и![]() … представляют собой последовательные
приближения
… представляют собой последовательные
приближения![]() к корню
к корню![]() .
.
Возможен также
(рис.4) другой вид ломаной
![]() («Спираль»). Легко заметить, что решение
в виде «лестницы» получается, если
производная
(«Спираль»). Легко заметить, что решение
в виде «лестницы» получается, если
производная![]() положительна, а решение в виде спирали,
если
положительна, а решение в виде спирали,
если![]() отрицательна.
отрицательна.
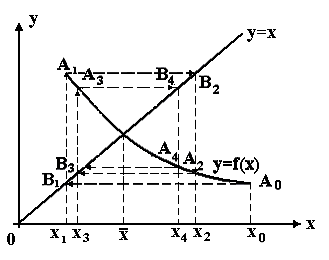
Рис.4
Если
![]() ,
то процесс итерации может быть расходящимся
(рис.5).
,
то процесс итерации может быть расходящимся
(рис.5).
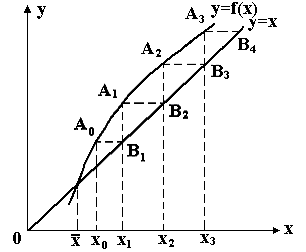
Рис. 5
Пусть теперь
требуется решить уравнение
![]() ,
причем примем для определенности, что
,
причем примем для определенности, что![]() ,
,![]() и на
и на![]() выполнено неравенство
выполнено неравенство
![]() ,
(8.4)
,
(8.4)
где
![]() и
и![]() – некоторые постоянные. Введем в
рассмотрение функцию
– некоторые постоянные. Введем в
рассмотрение функцию
![]() ,
,
где
![]() – некоторая постоянная и заметим, что
решение уравнения
– некоторая постоянная и заметим, что
решение уравнения![]() равносильно решению уравнения
равносильно решению уравнения![]() .
.
Так как
![]() ,
то, используя (8.4) будем иметь
,
то, используя (8.4) будем иметь
![]() .
.
Выберем теперь
число
![]() так, чтобы выполнялось неравенство
(8.3), т.е. потребуем выполнения двух
равенств
так, чтобы выполнялось неравенство
(8.3), т.е. потребуем выполнения двух
равенств
![]() ,
,![]() (8.5)
(8.5)
Решая систему
(8.5) двух уравнений относительно
![]() и
и![]() ,
получим
,
получим
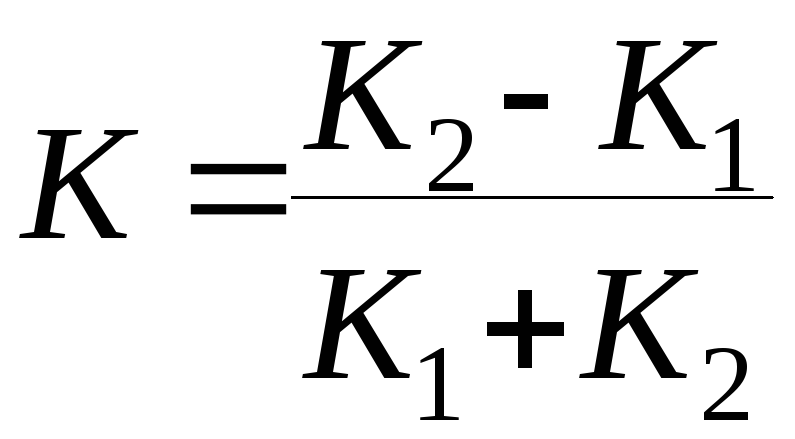 ,
,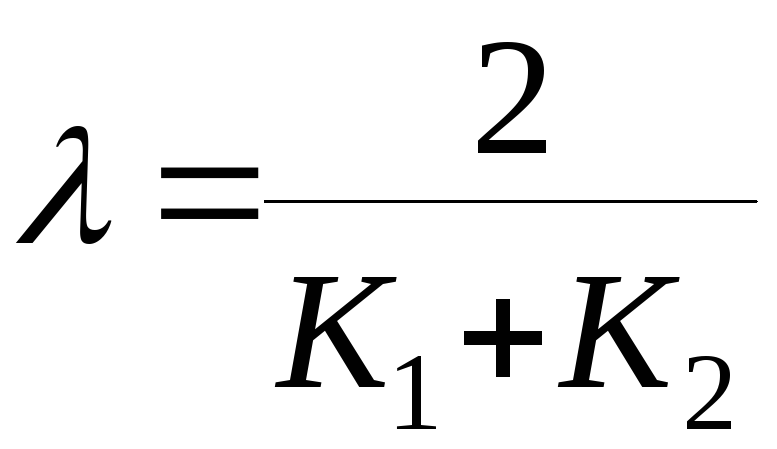 (8.6)
(8.6)
и заметим, что
условие
![]() выполнено.
выполнено.
Пример. Требуется найти приближенное значение корня уравнения
![]()
на промежутке
![]() .
.
Легко проверяется,
что
![]() ,
а
,
а![]() .
Выпишем производную
.
Выпишем производную![]() и заметим, что на промежутке
и заметим, что на промежутке![]() выполняется неравенство
выполняется неравенство
![]() ,
,
а тогда в соответствии с равенствами (8.6), получим
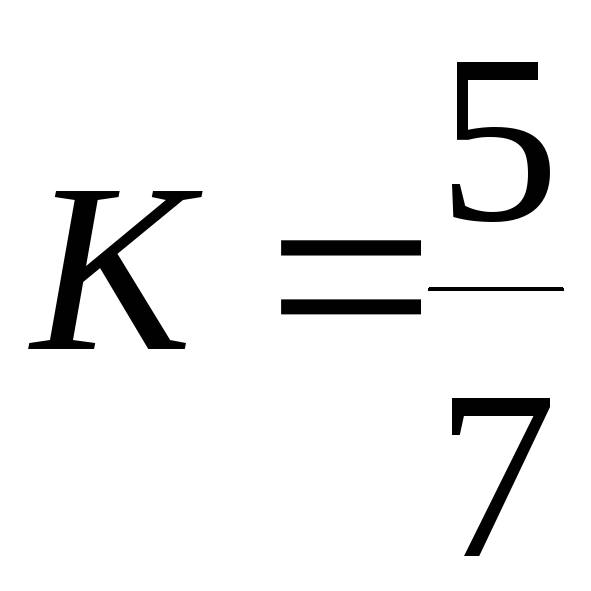 ,
,
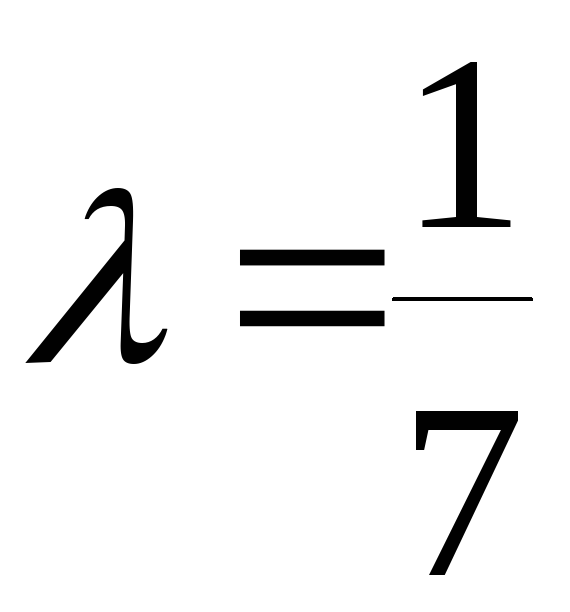 .
.
Введем в рассмотрение функцию
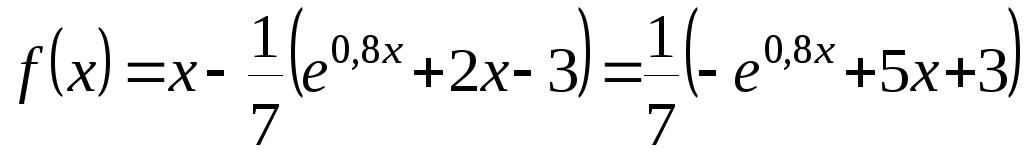
и используя метод
итераций положим сначала
![]() ,
а затем, производя вычисления с помощьюMathcad
Professional,
получим
,
а затем, производя вычисления с помощьюMathcad
Professional,
получим
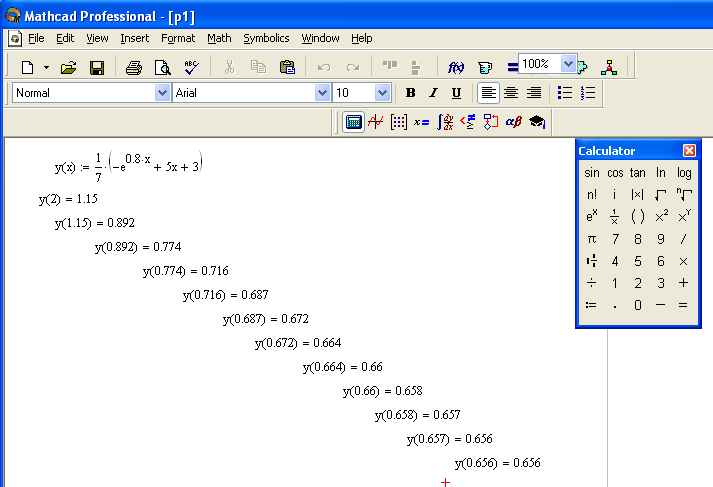
То есть для получения искомого решения проделали 12 шагов.
