§ 3. Малые колебания механических систем

Из курса «Теоретическая механика» известно, что положение механической системы с степенями свободы задается с помощьюобобщенных координат.

В случае голономных связей уравнения Лагранжа второго рода имеют вид:

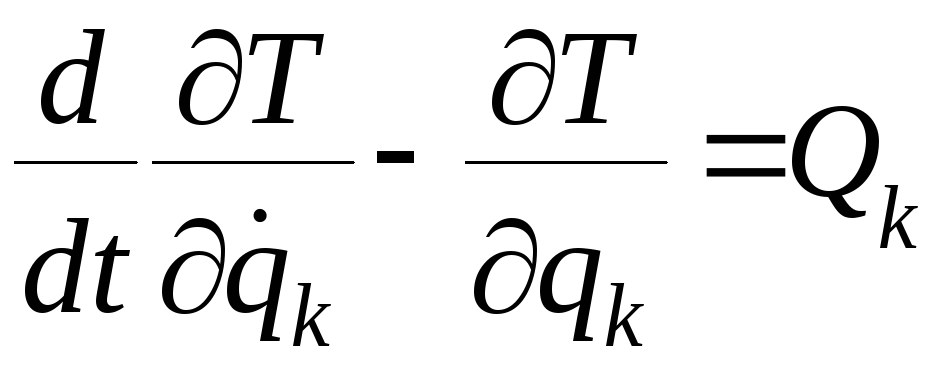,, (7.23)

где – обобщенные силы, а– кинетическая энергия системы, равная половине суммы произведений масс точек системы на квадрат их скоростей, то есть выражается в виде некоторой квадратичной формы относительно обобщенных скоростей

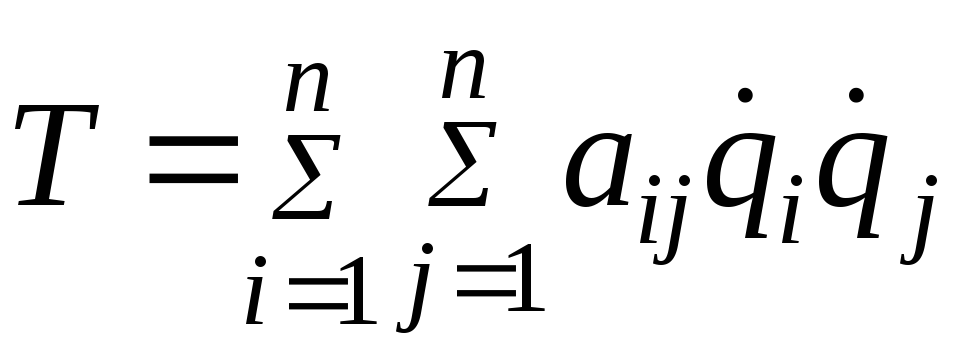, (7.24)

коэффициенты которой зависят от координат .

Для консервативных действующих сил элементарная работа равна уменьшению потенциальной энергии , которую также можно считать выраженной через обобщенные координаты, при этом

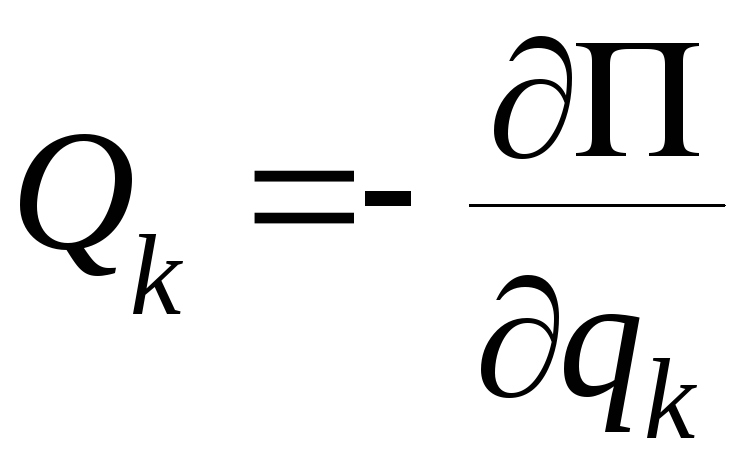,. (7.25)

Пусть точка означает состояние равновесия рассматриваемой системы. В состоянии равновесия, а тогда кинетическая энергия системы равна нулю и все ее частные производные потакже равна нулю, ибо они представляют собой линейные формы от. Отсюда следует, что левые части уравнений Лагранжа обращаются тождественно в нули и величиныудовлетворяют уравнениям

, ,

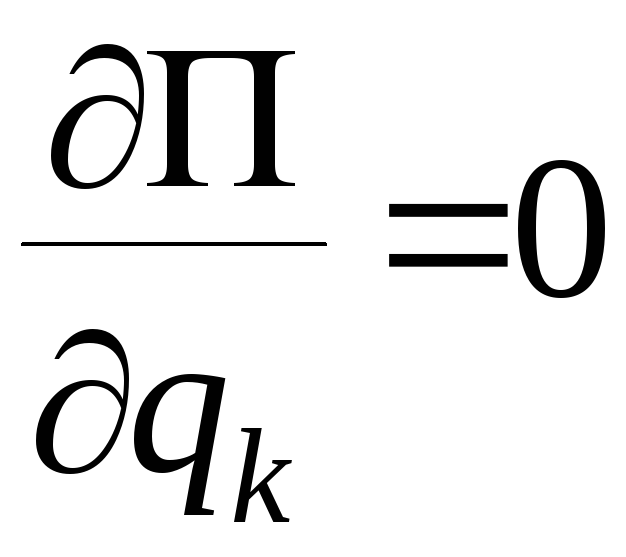то есть положения равновесия системы возможны только в стационарных точках потенциальной энергии. Можно показать, что точка минимума потенциальной энергии отвечает устойчивому положению равновесия. Рассмотрим такую точку. Без ограничения общности можно считать, что в этой точке и само значение потенциальной энергии также равно нулю. Если ограничиться изучением движения системы в малой окрестности нулевой точки, то коэффициенты квадратичной формыможно считать постоянными, равными своим значениям в нулевой точке. Если потенциальную энергиюразложить в ряд Тейлора в окрестности точкипо переменными отбросить члены выше второго порядка, то получим квадратичную форму относительно координатс постоянными коэффициентами (линейные члены относительнобудут отсутствовать, так как все частные производные отпов положении равновесия равны нулю), то есть

.

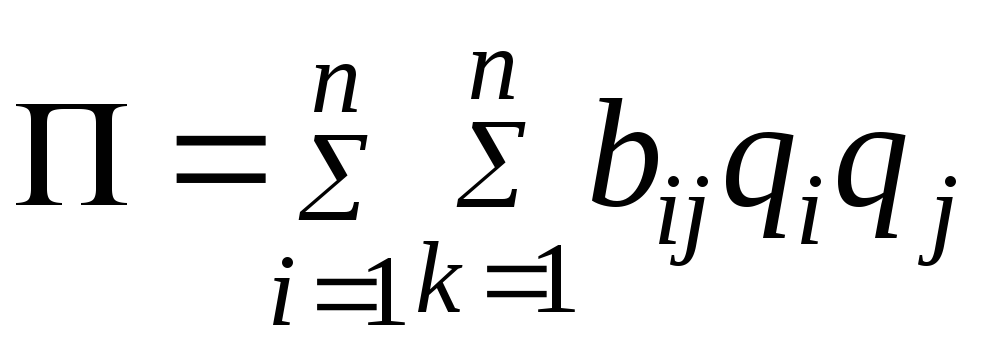Так как обе квадратичные формы иявляются положительно определенными, то существует линейное преобразование координатв координаты

, ,,

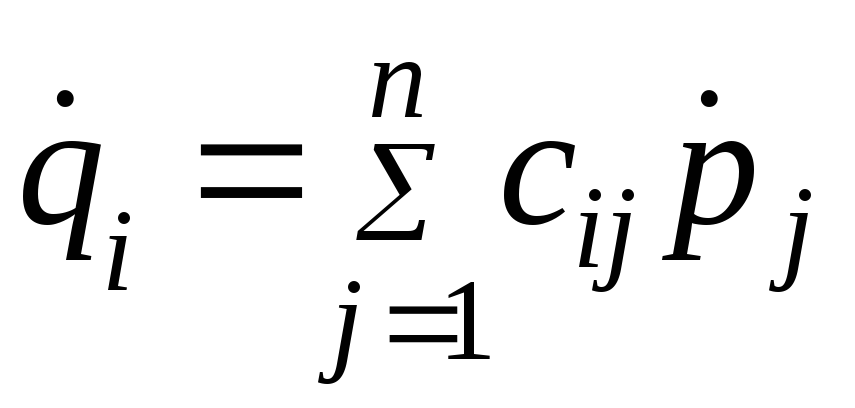приводящие квадратичные формы ик виду

,

.

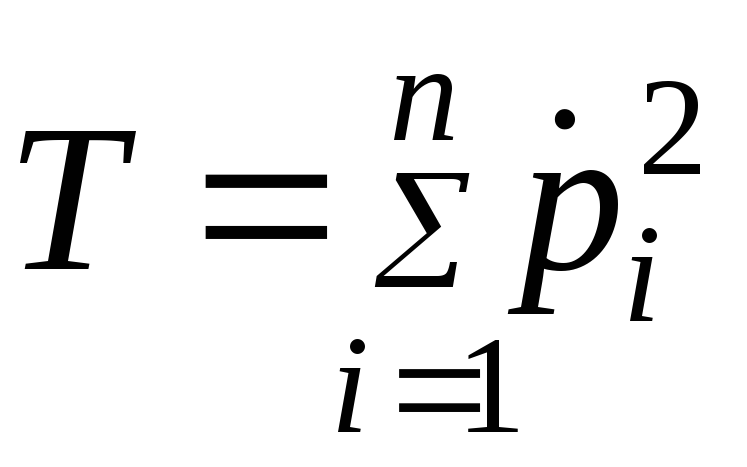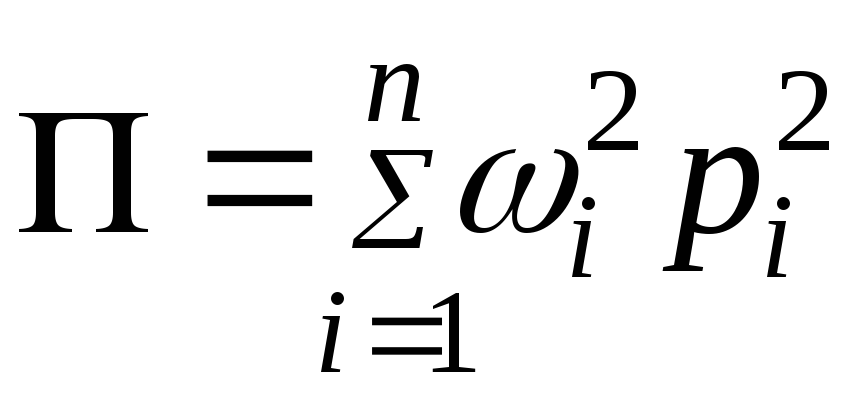В обобщенных координатах уравнения Лагранжа (7.23) с использованием примут вид

, ,

решения которых могут быть записаны в виде

,

где константы иопределяются из начальных условий. Величиныназываютсясобственными частотами системы. Следовательно, каждая из координат совершает гармонические колебания с собственной частотой.

Глава 8. Элементы теории метрических пространств § 1. Определение метрического пространства

Потребности науки и техники потребовали изучения значительно более общего понятия пространства по сравнению с эвклидовым пространством. Ниже мы рассмотрим основные понятия теории метрических пространств, то есть множеств, состоящих из элементов произвольной природы, на которое накладывается только одно требование: должно быть определено понятие расстояния между его элементами, удовлетворяющее некоторым условиям.

Определение. Метрическим пространством называется всякое множество элементов произвольной природы вместе с однозначной, неотрицательной, действительной функцией, определенной для любых элементовииз, удовлетворяющих следующим трем условиям:

1. тогда и только тогда, когда ;

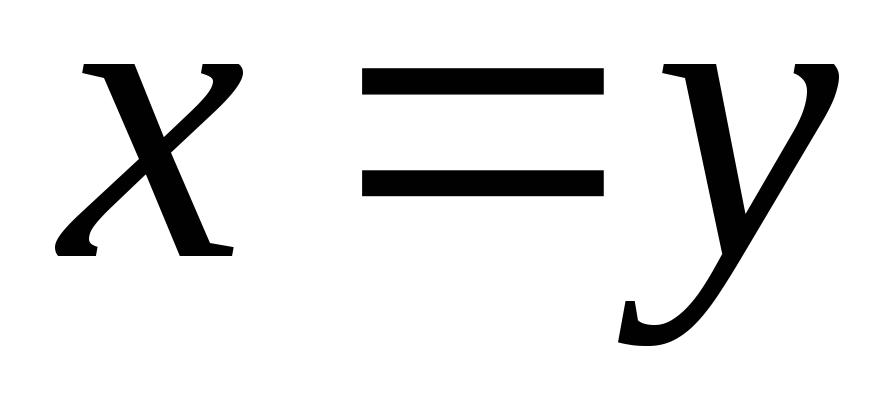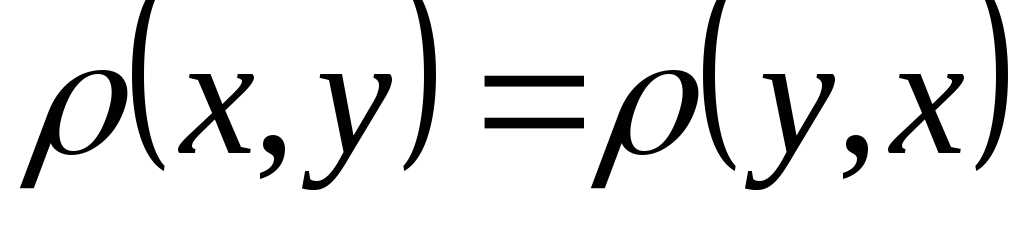2. аксиома симметрии;

3. для любых трех элементов 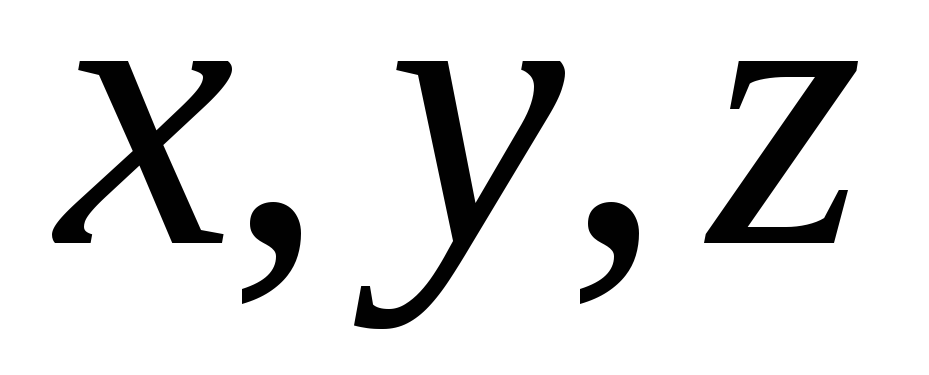выполняется неравенство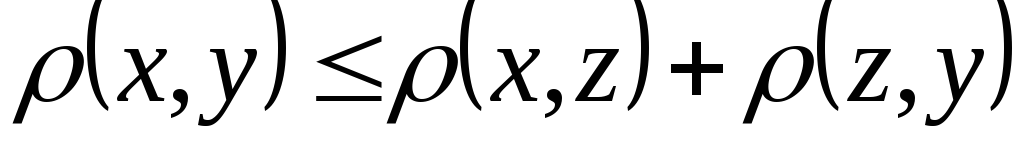аксиома треугольника.

Определение. Элементы иметрического пространстваназывают точками, функцию– расстоянием между точкамии, а само метрическое пространство, т.е. паруобозначают одной буквой.

Рассмотрим примеры.

Пример 1. Множество действительных чисел с расстоянием

образует метрическое пространство .

Пример 2. Множество всевозможных наборов из упорядоченных чисел вида,, принимаемых за точки,расстояния между которыми определяется равенством

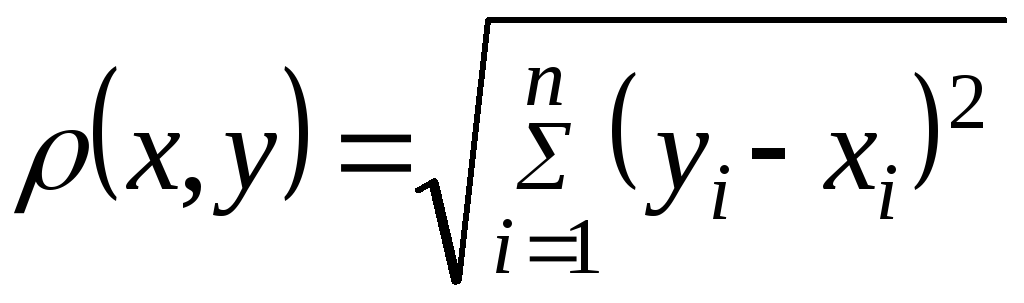
называется -мерным арифметическим евклидовым пространством.

Пример 3. Множество, точками которого является всевозможные последовательности

вещественных чисел, удовлетворяющие условию

,

а расстояние определяется равенством

,

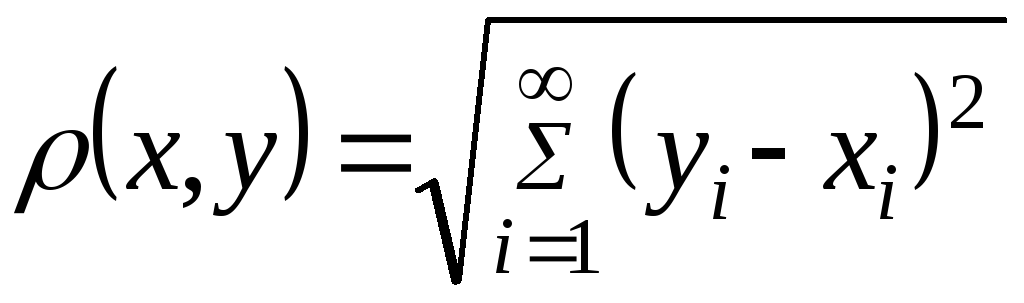является метрическим пространством, которое обозначают символом .

Пример 4. Множество всех непрерывных действительных функций определенных на промежутке , причем расстояние для любых двух элементовиопределено по формуле

,

т.е. в этом случае расстояние есть максимальное отклонение одной функции от другой. Это метрическое пространство обозначают символом .

Пример 5. Как и примере 4, рассмотрим множество всех функций непрерывных на , но расстояние определим иначе, а именно, положим

.

Такое метрическое пространство называют пространством непрерывных функций с квадратичной метрикой и обозначают символом .

Пример 6. Если для множества функций, рассмотренных в примерах 4 и 5, определять расстояние с помощью равенства

,

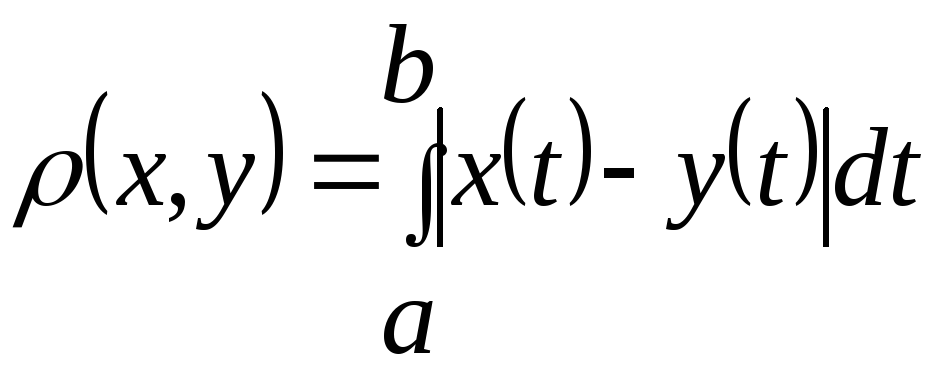то получим метрическое пространство, которое обозначают символом .

Из трех последних примеров следует, что метрические пространства, хотя и состоящие из одних и тех же элементов, но с различными определениями расстояний, следует считать различными.