§ 3. Метод наименьших квадратов

На практике часто возникает такая задача: известно, что величина линейно зависит от величинтак, что имеет место равенство

,

но коэффициенты неизвестны. Для их определения произведено с одинаковой точностьюзамеров (здесь) величины, то есть известны числаи соответствующие замеры величин, то есть известны числа. Это значит, что должны выполнятьсяуравнений системы (5.6). Но вследствие неизвестных ошибок при измерениях эта система будет, вообще говоря, несовместной. Возникает задача по определению коэффициентовтак, чтобы каждое уравнение удовлетворялось приблизительно, но с общей наименьшей погрешностью. Если за меру погрешности принять среднее квадратичное из отклонений величин

,

от известных величин , т.е. выражение (5.7), то придем к задаче, решенной в§ 2.

Пример

В «Основах химии» Д.И. Менделеева приводятся экспериментальные данные о растворимости азотно-кислого натрия в зависимости от температуры воды. В 100 частях воды растворялось следующее число условных

частей при соответствующих температурах

Температура воды	4°	10°	15°	21°	29°	36°
Число условных частей	71,0	76,3	80,6	85,7	92,9	99,4

Из теоретических соображений следует, что количественная сторона этого процесса может быть описана уравнением

, (5.14)

где – температура в градусах,– растворимость в условных частях на 100 частей воды, аи– неизвестны. Если подставить в уравнение (5.14) вместоисоответствующие числа из данной таблицы, то получим систему из шести уравнений

,

которая несовместна. В согласии с изложенным в п. 2 введем в рассмотрение 3 вектора

,,,

а затем вычислим 5 скалярных произведений

, ,,,

.

Система уравнений (5.11) в нашем случае примет вид

,

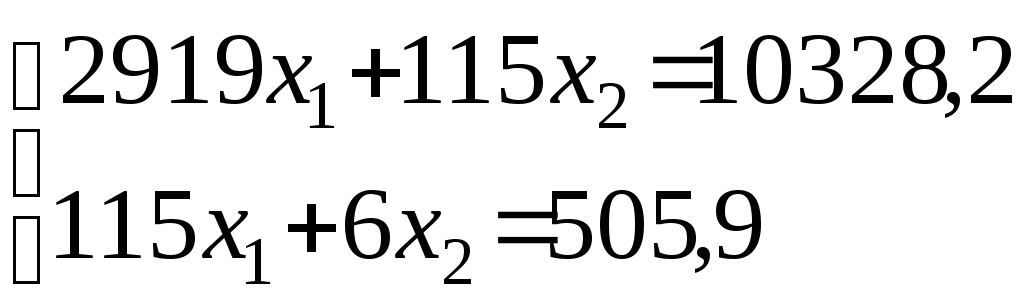решив которую получим ;, так что искомая зависимость примет вид

. (5.15)

Если подставить в уравнение значения температуры воды из данной таблицы, то получим числа условных частей

,

что свидетельствует о неплохом совпадении с экспериментальными данными.

Глава 6. Собственные векторы и собственные числа § 1. Определение собственных векторов и собственных чисел

Пусть в линейном пространстве задан линейный оператор.

Определение. Подпространство линейного пространстваназываетсяинвариантным относительно оператора , если для всякого вектора из подпространстваследует, что вектортак же принадлежит.

Рассмотрим некоторые примеры.

Пример 1. Для оператора подобия (линейный оператор , переводящий каждый векторв, где– фиксированное число, называется оператором подобия) каждое подпространство является инвариантным.

Пример 2. Пусть – базис в трехмерном пространстве, а– фиксированные числа. Определим оператордля векторов базиса условиями

, ,,

а для любого другого вектора условием

.

Этот оператор называется диагональным. Каждое подпространство, порожденное некоторыми из базисных векторов , является инвариантным для диагонального оператора.

Особую роль играют одномерные инвариантные подпространства оператора .

Определение. Всякий (ненулевой) вектор, принадлежащий одномерному инвариантному подпространству оператора называетсясобственным вектором оператора , то есть векторназываетсясобственным вектором оператора , если операторпереводит векторв коллинеарный ему вектор:

,

где число называетсясобственным значением (собственным числом) оператора , соответствующим собственному вектору.