6.3 Способы и точность определения площадей земельных участков

Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного кадастра.

В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют следующие способы определения площадей:

• аналитический - площадь- вычисляется по результатам измерений линии на местности, результат нм измерении линий и углов на местно­сти или по их функциям (координатам вершин фигур);

• графический - площадь вычисляется по результатам измерений линий или координат на плане (карте);

• механический - площадь определяется по плану с помощью спе­циальных приборов (планиметров) или приспособлений (палеток). Иногда эти способы применят комбинированно (например, часть линейных величин для вычисления площади определяют по плану, а часть берут из результатов измерений на местности).

Площади можно также определить на ЭВМ по цифровой модели местности по специальной программе.

При аналитическом способе определения площадей применяются формулы геометрии, тригонометрии и аналитической геометрии. При определении площадей небольших участков (для учета площадей, занятых строениями, усадьбами, площадей вспашки, посева) их разбивают на простейшие геометрические фигуры, преиму­щественно треугольники, прямоугольники, реже - трапеции. В этом случае площади участков определяются как суммы площадей отдель­ных фигур, вычисляемых по линейным элементам - высотам и ос­нованиям.

Если по границам участка выполнены геодезические измерения, то площадь всего участка или его части можно вычислить по приведенным применительно к следующим фигурам участков:

1) треугольник. Площадь треугольника определяется по сторонам 1, и 1₂, углу β₂ заключенному между ними, по формуле

Р=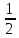 (I₁1₂ sin β₂); (1)

2) четырехугольник. В зависимости от элементов, известных в четырехугольнике, могут быть использованы различные формулы для расчета, в связи с чем приведем пример, характеризу­ющий это многообразие.

Пусть в четырехугольнике измерены все стороны и один угол при вершине 2. В таком случае площадь тре­угольника 1-2-3 может быть вычислена по формуле (1). При этом полезно вычислить длину 1_1-3 , используя теорему косинусов:

Площадь треугольника 1-3-4 может быть вычислена по формуле:

где - полупериметр.

Общая площадь четырехугольника

При наличии координат вершин полигона площади треугольни­ка и четырехугольника удобно вычислять соответственно по следу­ющим формулам:

(2)

Если полигон имеет более четырех углов, то площадь его быстрее и с хорошим контролем можно получить по координатам Х_i и У_i его вершин или по приращениям координат ΔХ, и ΔУ после увязки по­лигона, например по следующим формулам:

(3)

Координаты вершин полигона для определения площади участка как в государственной, так и в местной системах могут быть полу­чены любым из известных геодезических способов: триангуляцион­ными или линейно-угловыми построениями; проложением полиго­нометрических или теодолитных ходов; угловыми, линейными и полярными засечками; спутниковыми приемниками для определе­ния местоположения и т. д.

Кроме того, когда требуется определить только площадь или гра­ницы участка в его частной системе координат, можно применять так называемый способ изолированных базисов. Суть его заключается в том, что координаты точек объекта определяют засечками с изоли­рованных друг от друга базисов, расположенных в удобных местах внутри (рис.2, а) или вблизи (рис.2, б) участка.

Для приведе­ния результатов измерений в одну систему координат необходимо, чтобы было выполнено условие перекрытия, т. е. со смежных бази­сов должно быть определено несколько (минимум две) общин точек.

Для каждой из п общих точек смежных базисов, например Ь, и Ь₂, можно записать два уравнения связи вида:

Рис. 2. Определение координат точек участка с изолированных базисов, находящихся: а - внутри участка; б - вблизи участка

Хj⁽¹⁾=х_j⁽²⁾cos φ_1,2 -Y_j²sin φ_{1,2 +} х_с¹;

Yj⁽¹⁾= х_j⁽²⁾sin φ_1,2 + у_j²cos φ_1,2 + Y _с^{1 (4)}

из которых по методу наименьших квадратов определяется угол φ_{1,2 ,} разворота систем координат и координаты Х_с¹и Y _с¹ начала коорди­нат системы 2 в системе 1. Установив параметры преобразования ко­ординат, в правые части этих формул подставляют координаты и у₁⁽²⁾ остальных (т - п) точек, определенных со второго базиса, пе­реводя их тем самым в первую систему.

Аналогичным образом реша­ется задача для всех точек, определяемых с базисов Ь_З, Ь₄ и т. д.

При графическом способе определения площадей участок на плане делят на простейшие геометрические фигуры.

При разбивке участка на простейшие фигуры можно принять много вариантов, однако точность вычисления площади участка при различных вариантах не будет одинаковой. Площадь треугольника графическим способом вычисляется точнее площадей определяемых

разбивкой на прямоугольники, трапеции и другие фигуры.

Механический способ определения наиболее целесообразно применять для участков с ломаными линиями. Можно оп­ределить площади прямолинейными и криволинейными палетками. При определении площадей по плану графическим или механическим ^­ способом (с помощью планиметра и палеток) необходимо учитывать деформацию бумаги (плана). Величина деформации может характеризоваться коэффициентом q, определенным в двух взаимоперпендикулярных направлениях по следующей формуле:

q = , (5)

где L_о - теоретическая длина линии, значащаяся на плане (например, длина стороны квадрата координатной сетки); - результат измерения этой линии по плану.

В настоящее время механические планиметры заменили электронные (цифровые). Представляют интерес цифровые планиметры, например фирмы Topcon, которая предлагает несколько моделей цифровых планиметров, позволяющих проводить измерения площадей по картам или другим материалам с точностью ±0,2 % .

Если для определения площадей используются пункты государственной геодезической сети, то полученные площади чаще всего имеют немного преуменьшенное значение, потому что координаты пунктов относятся не к поверхности Земли, а к поверхности принятого референц – эллипсоида. На больших высотах этой разницей не всегда можно пренебречь.

Переход от площади Р₀ на поверхности референц – эллипсоида к площади Р на поверхности Земли на высоте Н может быть выпол­нен по формуле

Р=Ро,(6 ) где R - радиус Земли, равный 6 370 км.

Пользуясь координатами пунктов, планами (картами) в проекции Гаусса-Крюreра, площади участков Р_пР и размеры получаются всегда больше их горизонтальных проекций, и это увеличение возрастает по мере удаления от осевого меридиана зоны.

Для приведения площади к горизонтальной проекции используют формулу:

², (7) где У_m - средняя ордината участка (расстояние от осевого меридиа­на зоны до середины участка).

Приведенный способ изолированных базисов свободен от попра­вок за переход от поверхности референц-эллипсоида и проекции Га­усса-Крюгера, так как координаты точек базисов и границ участков определяются в частной системе, на физической поверхности Земли.

Иногда возникает необходимость получения площадей физиче­ской (топографической) поверхности участка Р_Ф, которая тем боль­ше отличается от площади горизонтального проложения участка Р _г.п, чем больше угол наклона v или уклон i местности. Для получения площади физической поверхности участка его разбивают на части с одинаковыми скатами, т. е. с равностоящими, и более или менее прямыми горизонталями. На каждой из этих частей в перпендику­лярном направлении к горизонталям определяют угол наклона или уклон и вычисляют площадь Р_Ф на физической поверхности земли по следующим формулам:

Р_ф=Р _г.п ;

Р_ф=Р _г.п (8).

Например, уже при угле наклона v = 2,9 (уклоне i = 0,05) поправка составит 1 : 800, или 12,5 м² на 1 га.

Требования к точности определения площади земельных участков зависят от многих факторов: хозяйственной значимости (сельскохозяйственные угодья, лесные угодья, городская территория и т. п.), местоположения (центр города, его окраина и т. п.), экологической обстановки (химическая загрязненность земли, атмосферы и т. п.), наличия и ценности недвижимости. Все эти и другие возмож­ные факторы влияют на нормативную стоимость земли, которая в основном и является исходной для расчета требуемой точности оп­ределения площади земельных участков.

Достижение требуемой точности возможно лишь при правильном выборе способа определения площади участка. Очевидно, что наивысшая точность может быть достигнута при аналитическом способе определения площади. При этом способе площадь участка определяется по результатам измерений на местности и погрешность в определении площади зависит от погрешностей этих измерений. Так, погрешность m_p площади треугольника и прямоугольника, вычисляемую по измеренным высоте h с погрешностью т_h и основанию 1 с погрешностью m_i , определяют по формуле (9). При одинаковой относительной погрешности измерения h и l

(9)

(10) Например, при Р =1 га (10 000 м²) и 1/S = 1/2 000 т_Р=7 м². Из выражений (23.3) для полигона с п вершинами можно получить фор­мулу погрешности площади вида

(11)

где m - средняя квадратическая погрешность определения коорди­нат х и у точек вершин полигона при условии, что

D_i - расстояние от начала координат до i-й точки вершины пол тона (в частном случае - от одной из вершин, принятой за начало координат).

Для прямоугольника со сторонами а и Ь формула (11) примет вид

(12)

а для квадрата со стороной а (13)

Например, если для участка размером 100 х 100 м и площадью 1 га определять координаты со средней квадратической погрешностью 0,02 м, то погрешность площади будет равна 2 м².

Для погрешности площади участка, определяемой по топографическому плану (карте), с учетом погрешностей измерений на м мости и погрешностей составления топографического плана мо использовать формулу следующего вида:

	Погрешность m, м2, для масштабов
Площадь Р, м2
	1:500	1:1000	1:2000
400	3,0	6,0	12,0
600	3,6	7,3	14,6
1200	5,2	10,4	20,8
2 500	7,5	15,0	30,0
10 000	15,0	30,0	60,0

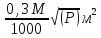= (14)

где М -знаменатель численного масштаба плана; Р - площадь участка.

В таблице приведены величины средних квадратических погреш­ностей, вычисленных по формуле (14) для различных площадей участков по планам различных масштабов.

Приведенные формулы являются приближенными, так как не учитывают возможных погрешностей исходных данных и зависимо­сти между входящими в них величинами. Однако они вполне доста­точны для предварительных (проектных) расчетов.

5.4 Понятие о геоинформационных системах

Появление современных высокопроизводительных компьютеров с их возможностью переработки, хранения и выдачи огромного количества информации предопределило возникновение нового направления в хозяйственной и управленческой деятельности челове­ка и новой науки - геоинформатики.

Первоначально понятие «геоинформационные системы» (ГИС) расшифровывалось как «географические информационные системы», поскольку оно появилось в недрах географической науки. Сейчас область использования далеко вышла за пределы географии и приставка «гео» свидетельствует лишь о том, что информация свя­зана с Землей и деятельностью человека на ней.

Таким образом, под геоинформационной системой чаще всего понимают компьютерное хранилище знаний о территориальном взаимодействии природы и общества, обеспечивающее сбор, хранение, обработку и визуализацию (зрительное представление) многих видов информации о явлениях в окружающем человека пространстве и во времени. К их числу относится информация из областей гeографии, информатики, гeодезии, картографии, земельного учета, управления, права, экологии и других наук.

Геоинформационные системы подразделяются:

• по территориальному охвату - на общенациональные и региональные;

• по целям использования – многоцелевые, специализированные, информационно-справочные, для нужд планирования, управления и др;

• по тематике - водных ресурсов, использования земель, лесопользования, туризму и др.

Особенно активно развиваются системы, ориентированные на кадастр.

Источниками информации для ГИС в основном являются гeoгpaфические и топографические карты и планы, аэрокосмические материалы, нормативные и правовые документы.

Современные ГИС, как правило, являются цифровыми и создаются с использованием специального программного обеспечения и объема данных, называемого базой данных.

База данных с цифровой карты включает в себя два варианта информации: пространственную, определяющую местоположение объекта, и семантическую (атрибутивную), описывающую свойства объекта.

Многoобразная пространственная информация в ГИС организуется в виде отдельных тематических слоев, отвечающих решению различных задач. Каждый слой может содержать информацию, относящуюся только к одной или нескольким темам. Например, для задач развития гoродской территории набор из отдельных слоев может включать в себя данные: о землевладениях и недвижимости; об объектах транспорта, образования, здравоохранения, культуры; инженерных сетях; рельефе; геодезических сетях и других объектах городского хозяйства.

Для представления карт и планов в компьютере используется пря­моугольная система координат. Каждая точка описывается одной парой координат: Х, У. Пользуясь координатной системой, можно представить точки, линии и полигоны в виде списка координат. При этом для представления земной поверхности на плоскости используются различные картографические проекции, например проекции Гаусса- Крюгера.

Данные с карты, плана вводятся в компьютер путем цифрования. Цифрование может быть выполнено либо путем оцифровки каждой характерной точки объекта, либо путем сканирования всего листа карты электронным сканером. Ввод в базу данных компьютера может также осуществляться с электронных геодезических приборов. Описательные характеристики объектов могут вводиться с клавиатуры компьютера.

Данные аэро- и космических съемок, записанные в цифровом виде, также могут быть введены в компьютер, минуя бумажную стадию.

5.5 . Геоинформационные системы в кадастре

Любой вид кадастра (земельный, градостроительный, водный лесной и др.) является геоинформационной системой, поскольку содержит совокупность достоверных и необходимых сведений о природном, хозяйственном и правовом положении земель и недр на базе картографической информации. Картографическая информации служит и для оценки количества, качества и стоимости земель, регистрации землепользования и землевладения, текущего контроля за землепользованием.

Информационная основа кадастра создается в результате инвентаризации земель и кадастровых съемок. Эти работы могут охватывать как большие территории (город, район, населенный пункт и т. п.), так и небольшие земельные участки.

Чтобы разместить большое количество сведений в единой информационной системе, кадастровая информация делится на элементарные слои, каждый из которых самостоятельно используется для решения конкретной задачи.

Для автоматизированной системы кадастра, основанной на применении ГИС, используются цифровые кадастровые карты, планы. Все объекты, представленные на кадастровой карте, плане, имею пространственную привязку, т. е. их положение определено в том системе координат, которая принята при создании карты. Описательные данные объекта (земельного участка) составляют содержание базы данных информационной системы. Для обозначения и связи объектов этой базы данных используются идентификаторы (кадастровые номера) участков.

Таким образом, цифровая кадастровая карта, представляя собой совокупность метрических (графических) и семантических (описательных) данных, является картографической частью информационной системы кадастра.

Определяя местоположение земельных участков, их границы площади, она используется как инструмент управления земельными ресурсами.

Таким образом, государственный земельный кадастр является геоинформационной системой, обеспечивая сбор, хранение и в земельной информации потребителям.