Курсовая Кинематика сложног движения точки

Таким образом, элементарная работа силы равна произведению элементарного перемещения на проекцию силы на это перемещение.

Поскольку ds = \dr\, то, согласно (15.85), d'A=\F\\dr\Qosa, или

Следовательно, элементарная работа силы равна скалярному произведению векторов силы и дифференциала радиус-вектора точки ее приложения.

Если скалярное произведение записать в аналитическом виде, то формулу (15.87) можно представить в следующем виде:

Полная работа силы. Полную работу силы F на перемещении точки из положения Мо в положение М определяют как предел суммы ее элементарных работ, т. е.

где d'Ak — работа силы F на k-м элементарном перемещении, на которые разбита криволинейная дуга МОМ.

Так как сумма (15.89) является интегральной суммой определения криволинейного интеграла, то

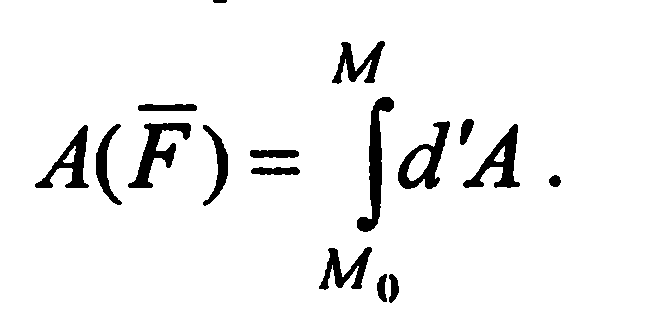
Используя различные формулы для определения элементарной работы, получаем

или

Если же сила является функцией времени, то, согласно (15.88), работа силы F на промежутке времени от 0 до t, соответствующем точкам М0 и А/, определяется выражением

Работа силы зависит от характера движения точки приложения силы. Так, А = 0, если сила приложена к неподвижной точке или к точке, скорость которой во время движения равна нулю (например, в МЦС).

Работа равнодействующей силы. Рассмотрим систему сил (F1F2...FN), приложенную к рассматриваемой точке. Эта система имеет равнодействующую R*, причем