Типы алгоритмов Линейные алгоритмы

Алгоритм, который содержит лишь указания о безусловном выполнении некоторой последовательности действий, без повторений или разветвлений (простое следование) называют линейным.

Рис. 10.1. Схематическое изображение линейного алгоритма

Рассмотрим задачу, которую можно формализовать с помощью линейного алгоритма.

1. Задача 1. При острых и хронических бронхитах; снижении аппетита, ухудшении пищеварения врач, в частности, рекомендует пациенту принимать травы душицы. Способ ее применения и дозы представлены на упаковке в виде текста следующего содержания: 10 г травы (2 ст. ложки) душицы помещают в эмалированную посуду, заливают 200 мл (1 стакан) кипяченной воды комнатной температуры, закрывают крышкой и настаивают на кипящей водяной бане 15 мин. Охлаждают при комнатной температуре 45 мин., процеживают, остаток отжимают в процеженный настой. Настой доливают кипяченной водой до 200 мл. Принимают в теплом виде по 1/2 стаканы 2 раза в день за 15 мин. до еды.

Реализация приведена задача изображена на рис.10.2

Рис. 10.2. Структурная схема линейного алгоритма

Разветвленные алгоритмы

Алгоритм, в котором предполагается проверка определенного утверждения называют разветвленным.

Разветвление– это такая форма организации действий, при которой в зависимости от выполнения или невыполнения некоторого условия осуществляется та или иная последовательность действий.

Условие– это любое утверждение или вопрос, который допускает лишь две возможные ответа “так” (истинное утверждение) или “нет” (утверждение ошибочное).

Для выполнения определенного указания S нужно сначала определить ошибочно или истинно утверждения Р. Если утверждение Р истинно, то выполняем указание S1 и на этом указание S заканчивается. Если же утверждение Р ошибочное, то выполняется указание S2 (или она не предусмотрена условием задачи) и на этом указание S заканчивается (рис 10.3 и 10.4).

Рис. 10.3. Полная форма разветвления. Рис. 10.4. Неполная форма разветвления

Рассмотрим задачу, которая формализована с помощью разветвленного алгоритма.

Задача 2. При диагностике заболевания желудочно-кишечного тракта определяют кислотность среды Рн, пользуясь следующими критериями: PH<7 - среда кислая, PH=7 - среда нейтральная, PH>7 - среда щелочная.

Реализация данной задачи изображена на рис. 10..5.

Р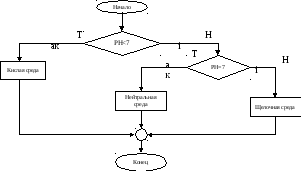ис. 10.5. Структурная схема разветвленного алгоритма

Циклические алгоритмы

Алгоритмы, в которых предусмотрено многоразовое повторение некоторой последовательности действий называют циклическими.

Цикл– это форма организации действия, при котором та самая последовательность действий выполняется несколько раз до тех пор, пока выполняется некоторое условие. Различают два типа циклов:

Цикл-ПОКА.

В структуре цикл-ПОКА для выполнения указания S сначала необходимо определить, истинно или ошибочно утверждения Р. Если Р истинно, то выполняется указание S1 и снова возвращаются к определению истинности утверждения Р. Если же утверждение Р ошибочно, то выполнение указания S считается законченным (рис. 10.6).

Цикл-ДО

В структуре цикл-ДО сначала выполняется указание S1, а потом определяется истинность утверждения Р. Если утверждение Р ошибочно, то снова выполняется указание S1 и определяется истинность утверждения Р. Если утверждение Р истинно, то выполнение указания S считается законченным (рис. 10.7).

Рис. 10.6. Цикл – ПОКА Черт. 10.7. Цикл – ДО

Рассмотрим задачу, которая формализована с помощью разветвленного алгоритма.

Задача 3. Подать графическим способом алгоритм определения значений давления крови в аорте в диапазоне 0≤ t ≤1 (c), с шагом ∆t=0.1 (c). Р₀ - начальное значение давления крови, х - гидравлическое сопротивление аорты, k - эластичность аорты.

Согласно условию задачи одно и то же действие выполняется многократно при последовательно возрастающем значении t.

Реализация данной задача изображена на рис. 10.8.

Рис. 10.8. Структурная схема циклического алгоритма.