2.3. Метод хорд в форме «ложного» положения. Расчетная формула метода хорд в форме «ложного» положения имеет вид :

,   n=0,1,…; ( 13 )

c - фиксированная точка (одна из границ интервала локализации изолированного корня ).

На практике для монотонной сходимости метода необходимо :

1. 1-ая производная f(x) должна быть знакопостоянна на интервале локализации [ a , b ] изолированного корня ;

2. 2-ая производная f(x) должна быть знакопостоянна на интервале локализации [ a , b ] изолированного корня ;

3. за начальное приближение x₀ выбирается та граница интервала локализации , на которой произведение функции на ее 2-ю производную меньше нуля ( f( c)f^’’(c) < 0 , где с – одна из границ интервала ) .

4. за неподвижную точку ( точку «ложного положения» ) c выбирается та граница интервала локализации , на которой произведение функции на ее 2-ю производную больше нуля

( f( c)f^’’(c) > 0 , где с – одна из границ интервала ) .

 

Критерий окончания итерационного процесса. При заданной точности

>0 вычисления следует вести до тех пор пока не окажется выполненным неравенство

. ( 14 )

3. Решение нелинейных уравнений итерационными методами в среде системы Mathcad.

Найти приближенное значение изолированного корня нелинейного уравнения

x³- cos(x)+1 = 0 c точностью ε=10^{- 9}.

Задание нелинейной функции

Настройка системы Mathcad

, так как ε=10^{- 9} - заданная точность.

Количество цифр в результате после разделяющей точки произвести на вкладке Результат диалогового окнаКоличество десятичных позиций командыФормат  Результат.

Установить равным 10 (по умолчанию равно 3) , что на 1 больше порядка величины TOL – для возможности округления конечного результата .

- индексацию элементов начинать с нуля ( по умолчанию ORIGIN=0 ) .

Локализация изолированного корня

Построение графика функции

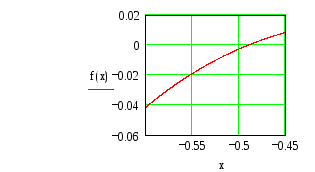
Интервал локализации изолированного корня

Проверка существования изолированного корня на интервале [ a ,b ] локализации корня

Проверка на знакопостоянство 1-ой и 2-ой производной функции f(x) на интервале [ a ,b ] локализации корня.

Создание функций 1-ой и 2-ой производной функции f(x).

Построение графиков 1-ой и 2-ой производной функции f(x)

В том случае , если условия закопостоянства производных на интервале [ a ,b ] не выполняются , то необходимо уменьшить его величину и задать новые значения a и b .

Метод Ньютона

Задание количество итераций

Правило выбора и задание х₀

Выполнение итераций

Проверка критерия окончания итерационного процесса .

1 - да , 0 – нет.

Значение корня

Корень с точностью ε=10^{- 9} найден за 6 итераций .

Метод простой итерации

Задание количество итераций

Преобразование нелинейного уравнения к виду метода простой итерации ( разрешение относительно х ) , то есть приведение к виду х= φ(х).

Построение 1-ой производной функции φ(х)

Проверка сходимости метода

Системная ошибка при построении графика .

Задание начального приближения

Выполнение итераций

Проверка критерия окончания итерационного процесса .

1 - да , 0 – нет.

Значение корня

Корень с точностью ε=10^{- 9} найден за 48 итераций .

Метод простой итерации с итерационным параметром

Построение графика 1-ой функции f(x)

Вычисление значения модуля и определение знака итерационного параметра α

Задание количество итераций

Задание начального приближения

Выполнение итераций

Проверка критерия окончания итерационного процесса .

1 - да , 0 – нет.

Значение корня

Корень с точностью ε=10^{- 9} найден за 48 итераций .