Тема 3. Векторна алгебра

Варіант 1

1) Знайти координати точки , якщо вектормає координату

кінця вектора .

2) Знайти проекцію вектора на вектор.

3) Знайти векторний добуток векторів і.

Варіант 2

1) Знайти координати точки , якщо вектормає координату початку.

2) Знайти проекцію вектора на вектор.

3) Знаючи, що і, знайти.

Варіант 3

1) Записати координати напрямного вектора, що йде бісектрисою другого октанта.

2) За яких умов на івекторитапаралельні?

3) Знайти змішаний добуток векторів і.

Варіант 4

1. Записати координати одиничного напрямного вектора, що йде бісектрисою третього октанта.

2) За яких умов на івекторитапаралельні?

3) Знайти змішаний добуток векторів і.

Варіант 5

1. Вектор, довжина якого дорівнює 3, має однакові координати. Знайти його.

2. Дано вектори і. Знайти кут, який утворює векторз віссю.

3. Вектори івзаємно перпендикулярні. Знаючи, що, обчислити .

Варіант 6

1. До однієї точки прикладені дві сили і, що діють під кутом 120⁰, причому ,. Знайти величину рівнодійної.

2. Дано два вектори і. Знайти проекції на координатні осі вектора.

3. Задані вектори . Знайти координати вектора

.

Варіант 7

1. Знайти довжину вектора , якщоі.

2. Обчислити площу паралелограма, побудованого на векторах .

3. Задані і. Знайти скалярний добуток.

Варіант 8

1. Знайти одиничний вектор, який перпендикулярний до векторів і.

2. Дано вершини чотирикутника А(2; -1; 2), В(2; 5; 0), С(-3; 2; 1),

D(-4; -4; 3). Знайти кут між діагоналями цього чотирикутника.

3. Задані координати точок А(4; 1; 4), В(3; 4; 1), С(5; 4; 3). Знайти координати векторного добутку .

Варіант 9

1) При яких значеннях івекториіколінеарні.

2) Визначити, при якому значенні t вектори івзаємно перпендикулярні.

3) Обчислити площу трикутника з вершинами А(4; 2; 3), В(5; 1; 2),

С(6; 5; 8).

Варіант 10

1. Знайти довжину вектора , якщоі.

2. Задані вершини трикутника А(0; -1; 4), В(-3; -1; 0), С(4; -1; 1). Визначити його внутрішній кут при вершині В.

3. Вектори іутворюють кут 120⁰, . Обчислити.

Варіант 11

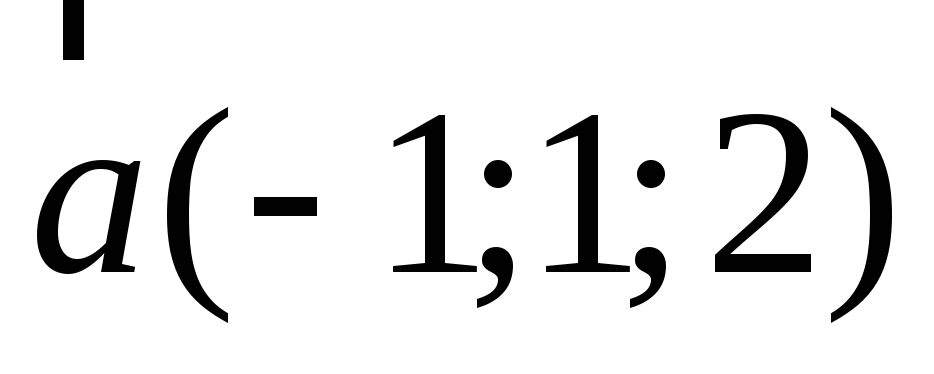1. При яких значеннях векториі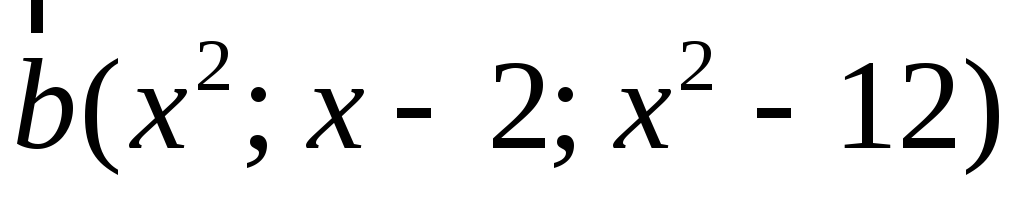колінеарні.

2. Вектор , перпендикулярний до векторіві, утворює з віссю ОУ тупий кут і має довжину. Знайти його координати.

3. Обчислити мішаний добуток векторів .

Варіант 12

1. Дано точки А(-1; 3; -3), В(4; 3; 6), С(2; 0; 3), D(4; 3; -3). Знайти проекцію вектора на вектор.

2. Дано три вектори і. Обчислити проекцію векторана вектор().

3. Визначити, якою трійкою є трійка векторів, лівою чи правою .

Варіант 13

1. При яких значеннях векториіперпендикулярні.

2. Знайти кут між ненульовими векторами і, якщо,і справедлива рівність.

3. З’ясувати лінійну залежність векторів .

Варіант 14

1. Визначити при яких значеннях івекториіколінеарні.

2. Вектори іутворюють кут 30⁰, причому . Знайти кут між векторамиі.

3. Знайти об’єм паралелепіпеда, побудованого на векторах ,.

Варіант 15

1. Заданий вектор . Знайти координати вектора, який лежить у площині ХОУ і перпендикулярний до вектора, якщо.

2. Знайти кут між діагоналями паралелограма, побудованого на векторах і

3. Знайти об’єм паралелепіпеда, побудованого на векторах ,.

Варіант 16

1) Знайти координати точки , якщо вектормає координату кінця.

2) Знайти проекцію вектора на вектор.

3) Знайти векторний добуток векторів і.

Варіант 17

1) Знайти координати точки , якщо вектормає координату початку.

2) Знайти проекцію вектора на вектор.

3) Знаючи, що і, знайти.

Варіант 18

1) Записати координати напрямного вектора, що йде бісектрисою третього октанта.

2) За яких умов на івекторитапаралельні?

3) Знайти змішаний добуток векторів і.

Варіант 19

1) Записати координати одиничного напрямного вектора, що йде бісектрисою п’ятого октанта.

2) За яких умов на івекторитапаралельні?

3) Знайти довжини діагоналей паралелограма побудованого на векторах .

Варіант 20

1) Вектор, довжина якого дорівнює 1, має однакові координати. Знайти його.

2) Дано вектори і. Знайти косинус кута, який утворює векторз віссю.

3) Вектори івзаємно перпендикулярні. Знаючи, що, обчислити .

Варіант 21

1) До однієї точки прикладені дві сили і, що діють під кутом 120⁰, причому ,. Знайти величину рівнодійної.

2) Дано два вектори і. Знайти проекції на координатні осі вектора.

3) Задані вектори . Знайти координати вектора

.

Варіант 22

1) Знайти довжину вектора , якщоі.

2) Обчислити площу паралелограма, побудованого на векторах .

3) Задані і. Знайти скалярний добуток.

Варіант 23

1) Знайти одиничний вектор, який перпендикулярний до векторів і.

2) Дано вершини чотирикутника А(2; -1; 2), В(2; 5; 0), С(-3; 2; 1), D(-4; -4; 3). Знайти кут між діагоналями цього чотирикутника.

3) Задані координати точок А(4; 1; 4), В(3; 4; 1), С(5; 4; 3). Знайти координати векторного добутку .

Варіант 24

1) При яких значеннях івекториіколінеарні.

2) Визначити, при якому значенні t вектори івзаємно перпендикулярні.

3) Обчислити площу трикутника з вершинами А(4; 2; 3), В(5; 1; 2),

С(6; 5; 8).

Варіант 25

1. Знайти довжину вектора , якщоі.

2. Задані вершини трикутника А(0; -1; 4), В(-3; -1; 0), С(4; -1; 1). Визначити його внутрішній кут при вершині В.

3. Вектори іутворюють кут 120⁰, . Обчислити.

Варіант 26

1. При яких значеннях вектори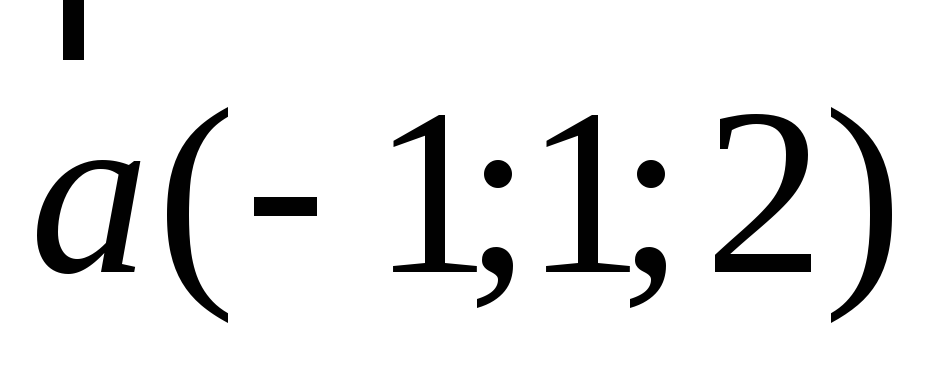іколінеарні.

2. Вектор , перпендикулярний до векторіві, утворює з віссю ОУ тупий кут і має довжину. Знайти його координати.

3. Обчислити мішаний добуток векторів .

Варіант 27

1) Дано точки А(-1; 3; -3), В(4; 3; 6), С(2; 0; 3), D(4; 3; -3). Знайти проекцію вектора на вектор.

2) Дано три вектори і. Обчислити проекцію векторана вектор().

3) Визначити, якою трійкою є трійка векторів, лівою чи правою .

Варіант 28

1) При яких значеннях векториіперпендикулярні.

2) Знайти кут між ненульовими векторами і, якщо,і справедлива рівність.

3) З’ясувати лінійну залежність векторів .

Варіант 29

1) Визначити при яких значеннях івекториіколінеарні.

2) Вектори іутворюють кут 30⁰, причому . Знайти кут між векторамиі.

3) Знайти об’єм паралелепіпеда, побудованого на векторах ,.

Варіант 30

1)Заданий вектор . Знайти координати вектора, який лежить у площині ХОУ і перпендикулярний до вектора, якщо.

2) Знайти кут між діагоналями паралелограма, побудованого на векторах і

3) Знайти об’єм паралелепіпеда, побудованого на векторах ,.