
- •Міністерство освіти і науки україни львівський національний аграрний університет
- •Вища математика
- •Львів 2015
- •Розрахунково-графічна робота №1
- •Тема 1. Матриці та визначники
- •Тема 2. Ранг матриці. Системи лінійних рівнянь
- •Тема 3. Векторна алгебра
- •Тема 4. Комплексні числа
- •Тема 5. Аналітична геометрія на площині
- •Тема 6. Аналітична геометрія в просторі
- •Розрахунково-графічна робота №2
- •Тема 7. Границі функцій
- •Тема 8. Похідна та її застосування
- •Тема 9. Невизначений інтеграл
- •Тема 10. Визначений інтеграл
- •Розрахунково-графічна робота №3
- •Тема 11. Функції багатьох змінних
- •Тема 12. Кратні і криволінійні інтеграли
- •Тема 13. Диференційні рівняння
- •Тема 14. Ряди
- •Розрахунково-графічна робота №4
- •Тема 15. Теорія ймовірностей
- •Бібліографічний список
- •Додатки
Тема 14. Ряди
Варіант 1
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 2
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 3
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
![]() ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 4
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 5
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 6
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 7
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 8
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 9
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 10
1.
Записати кілька перших членів ряду

2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Тейлора функцію
![]() за степенями
за степенями![]() .
.
5. Знайти три перших (відмінних від нуля) члени розвинення в ряд розв'язку рівняння, які задовольняють початкові умови
![]() .
.
Варіант 11
1.
Записати кілька перших членів ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Тейлора функцію
![]() за степенями
за степенями![]() .
.
5. Знайти три перших (відмінних від нуля) члени розвинення в ряд розв'язку рівняння, які задовольняють початкові умови
![]() .
.
Варіант 12
1.
Записати кілька перших членів ряду
 .
.
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Тейлора функцію
![]() за степенями
за степенями![]() .
.
5. Знайти три перших (відмінних від нуля) члени розвинення в ряд розв'язку рівняння, які задовольняють початкові умови
![]() .
.
Варіант 13
1.
Записати кілька перших членів ряду
 .
.
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Тейлора функцію
![]() за степенями
за степенями .
.
5. Знайти три перших (відмінних від нуля) члени розвинення в ряд розв'язку рівняння, які задовольняють початкові умови
![]() .
.
Варіант 14
1. Перевірити чи виконується необхідна умова збіжності ряду
 .
.
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Тейлора функцію
![]() за степенями
за степенями![]() .
.
5. Знайти три перших (відмінних від нуля) члени розвинення в ряд розв'язку рівняння, які задовольняють початкові умови
![]() .
.
Варіант 15
1. Перевірити чи виконується необхідна умова збіжності ряду
 .
.
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Тейлора функцію
![]() за степенями
за степенями![]() .
.
5. Знайти три перших (відмінних від нуля) члени розвинення в ряд розв'язку рівняння, які задовольняють початкові умови
![]() .
.
Варіант 16
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.Обчислити
з точністю до
![]() інтеграл
інтеграл .
.
Варіант 17
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
![]() .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 18
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 19
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 20
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 21
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 22
Написати найпростішу формулу
 го
члена ряду
го
члена ряду
![]()
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.Знайти інтервал та область збіжності ряду
 .
.Розвинути в ряд Маклорена функцію
 .
.Обчислити з точністю до
 інтеграл
інтеграл .
.
Варіант 23
1.
Написати найпростішу формулу
![]() го
члена ряду
го
члена ряду
![]()
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Маклорена функцію
![]() .
.
5.
Обчислити з точністю до
![]() інтеграл
інтеграл .
.
Варіант 24
Написати найпростішу формулу
 го
члена ряду
го
члена ряду
![]()
Дослідити ряди на збіжність: а)
 ;
б)
;
б)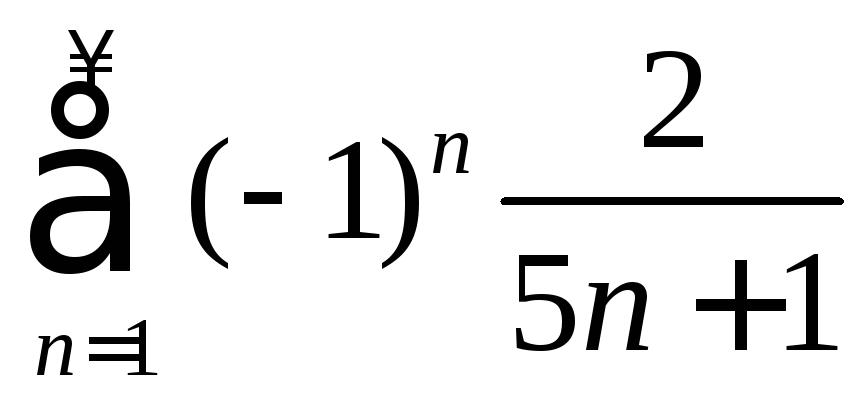 .
.Знайти інтервал та область збіжності ряду
 .
.Розвинути в ряд Маклорена функцію
 .
.Обчислити з точністю до
 інтеграл
інтеграл .
.
Варіант 25
1.
Записати кілька перших членів ряду

2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Тейлора функцію
![]() за степенями
за степенями![]() .
.
5. Знайти три перших (відмінних від нуля) члени розвинення в ряд розв'язку рівняння, які задовольняють початкові умови
![]() .
.
Варіант 26
1.
Записати кілька перших членів ряду

2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Тейлора функцію
![]() за степенями
за степенями![]() .
.
5. Знайти три перших (відмінних від нуля) члени розвинення в ряд розв'язку рівняння, які задовольняють початкові умови
![]() .
.
Варіант 27
Записати кілька перших членів ряду

Дослідити ряди на збіжність: а)
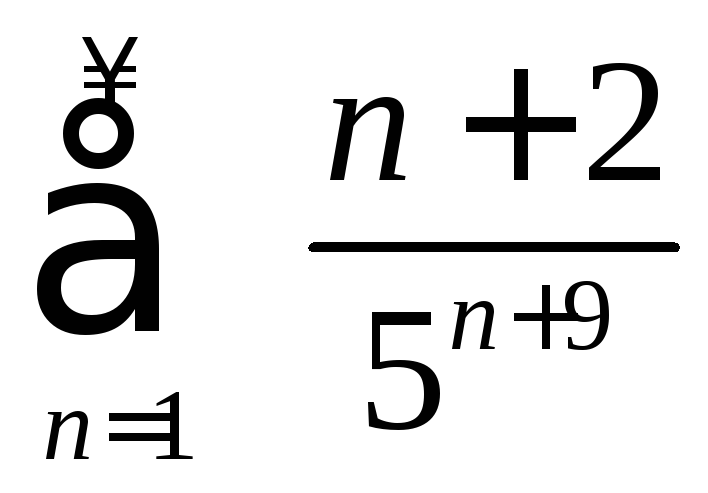 ;
б)
;
б) .
.Знайти інтервал та область збіжності ряду
 .
.Розвинути в ряд Тейлора функцію
 за степенями
за степенями .
.Знайти три перших (відмінних від нуля) члени розвинення в ряд розв'язку рівняння, які задовольняють початкові умови
![]() .
.
Варіант 28
1.
Записати кілька перших членів ряду
 .
.
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Тейлора функцію
![]() за степенями
за степенями .
.
5. Знайти три перших (відмінних від нуля) члени розвинення в ряд розв'язку рівняння, які задовольняють початкові умови
![]() .
.
Варіант 29
1. Перевірити чи виконується необхідна умова збіжності ряду
 .
.
2.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.
3.
Знайти інтервал та область збіжності
ряду
 .
.
4.
Розвинути в ряд Тейлора функцію
![]() за степенями
за степенями![]() .
.
5. Знайти три перших (відмінних від нуля) члени розвинення в ряд розв'язку рівняння, які задовольняють початкові умови
![]() .
.
Варіант 30
Перевірити чи виконується необхідна умова збіжності ряду
![]() .
.
Дослідити ряди на збіжність: а)
 ;
б)
;
б) .
.Знайти інтервал та область збіжності ряду
 .
.Розвинути в ряд Тейлора функцію
 за степенями
за степенями .
.Знайти три перших (відмінних від нуля) члени розвинення в ряд розв'язку рівняння, які задовольняють початкові умови
![]() .
.
