
- •Розрахунок електричного поля паралельних проводів Постановка задачі Розрахунок електричного поля паралельних проводів
- •Таблиця 8.1
- •Визначення ємнісних коефіцієнтів
- •Визначення часткових ємностей
- •Розрахунок поля півсферичного електрода
- •Розрахунок магнітного поля двопровідної лінії Постановка задачі
- •Визначення напруженості поля паралельних проводів
- •Визначення сили взаємодії проводів при короткому замиканні в мережі
- •Побудова графічної картини напруженості поля паралельних проводів
- •Визначення сили взаємодії трьох проводів зі струмами
Розрахунок електричного поля паралельних проводів Постановка задачі Розрахунок електричного поля паралельних проводів
Завдання
Лінія
передачі складається з трьох паралельних
проводів. Радіус кожного проводу рівний
 (рис. 8.29). Висоти підвісу проводів:
(рис. 8.29). Висоти підвісу проводів: ,
, ,
, .
Відстані між проводами по горизонталі:
.
Відстані між проводами по горизонталі: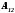 ,
, ,
, .
Потенціали проводів:
.
Потенціали проводів: ,
, ,
, .
.
Визначимо для кожного проводу:
1)
потенціальні коефіцієнти
 ;
;
2) ємнісні
коефіцієнти
 ;
;
3) часткові
ємності
 ;
;
4) лінійні
заряди на одиницю довжини
 .
.

Розрахунок електростатичного поля системи заряджених тіл проведемо за числовими даними, наведеними в табл. 8.1.
Таблиця 8.1
|
|
|
|
|
|
|
|
|
|
|
6 |
1.9 |
1,6 |
6.5 |
6.2 |
6.7 |
24 |
-4 |
-21 |
Визначення потенціальних коефіцієнтів
Найкоротші відстані між проводами у просторі рівні гіпотенузам прямокутних трикутників, де одним катетом є різниця висот підвісу проводів, а другим – відстань між проводами по горизонталі:
Відстань між проводом 1 і дзеркальним зображенням проводу 2 рівна гіпотенузі прямокутного трикутника, одним катетом якого є сума висот підвісу проводів, а другим – відстань між проводами по горизонталі (рис. 8.29):
Аналогічно визначаються відстані між проводом 1 і дзеркальним зображенням проводу 3; проводом 2 і дзеркальним зображенням проводу 3:
Потенціальні коефіцієнти проводів на одиницю довжини лінії визначаємо за формулами (8.63):
Одержані значення потенціальних коефіцієнтів дають можливість визначити потенціали проводів за відомими їхніми лінійними зарядами на одиницю довжини з системи рівнянь (8.62).
Якщо необхідно визначити лінійні заряди проводів, коли відомі їхні потенціали, то зручно користуватись системою рівнянь:
 (8.69)
(8.69)
Визначення ємнісних коефіцієнтів
Розв’яжемо
систему рівнянь (8.62) відносно лінійних
зарядів
 :
:

У системі
рівностей (8.69, а)
позначено через
 детермінант (визначник) системи рівнянь
(8.62), який складається з потенціальних
коефіцієнтів
детермінант (визначник) системи рівнянь
(8.62), який складається з потенціальних
коефіцієнтів :
:
(8.70)
Прирівнявши
у перших рівняннях систем (8.69) і (8.69, а)
коефіцієнти перед потенціалами
 ,
, і
і ,
одержуємо вирази для визначення ємнісних
коефіцієнтів
,
одержуємо вирази для визначення ємнісних
коефіцієнтів :
:
Оскільки,
відповідно до (8.63, а)
симетричні потенціальні коефіцієнти
 рівні, тобто:
рівні, тобто:
 ;
;
 ;
; ,
,
то, відповідно, будуть рівні та симетричні ємнісні коефіцієнти:
Шляхом
аналогічного прирівнювання у других і
третіх рівняннях систем (8.69) і (8.69, а)
коефіцієнтів перед потенціалами
 ,
, і
і ,
одержимо:
,
одержимо:
Визначення часткових ємностей
Систему
рівнянь (8.69) часто записують у такій
формі, щоб у правих частинах рівнянь
були не потенціали
 проводів, а різниці потенціалів між
проводами та між проводами і землею.
Тоді зв’язок між потенціалами
проводів, а різниці потенціалів між
проводами та між проводами і землею.
Тоді зв’язок між потенціалами і лінійними зарядами
і лінійними зарядами проводів за допомогою часткових ємностей
проводів за допомогою часткових ємностей виразиться
рівняннями:
виразиться
рівняннями:
 (8.71)
(8.71)
Розкривши
дужки в правих частинах рівнянь системи
(8.74) і, враховуючи, що потенціал землі
 ,
одержуємо:
,
одержуємо:
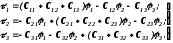 (8.71,
а)
(8.71,
а)
Прирівнюючи
у відповідних рівняннях систем (8.71, а)
і (8.69) коефіцієнти перед потенціалами
 ,
, і
і ,
одержуємо:
,
одержуємо:
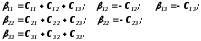
Враховуючи
обчислені значення ємнісних коефіцієнтів
 і рівність симетричних коефіцієнтів
(
і рівність симетричних коефіцієнтів
( ,
,
 ,
, )
з останніх рівнянь визначаємо значення
часткових ємностей проводів:
)
з останніх рівнянь визначаємо значення
часткових ємностей проводів:

 ,
м
,
м ,
м
,
м ,
м
,
м ,
м
,
м ,
м
,
м ,
м
,
м ,
кВ
,
кВ ,
кВ
,
кВ ,
кВ
,
кВ