
ФПП лаб
.pdf
Министерство образования и науки Российской Федерации НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
53 |
№ 3075 |
Ф 503 |
|
ФИЗИКА ТВЕРДОГО ТЕЛА
Методическое руководство к лабораторным работам по физике для студентов
I – II курсов РЭФ, ФТФ, ФЭН
всех специальностей и всех форм обучения
НОВОСИБИРСК
2006
УДК 539.2(076.5) Ф 503
Составили:
д-р. тех.наук, проф. А.А. Корнилович, канд. физ.-мат. наук, доц. В.Н. Холявко, канд. тех. наук, доц. Е.И. Уваров,
канд. физ.-мат. наук, ст. преп. А.П. Буриченко, канд. тех. наук, доц. В.И. Ознобихин
Рецензент: доктор физ.-мат. наук, проф. О.В. Кибис
Работа подготовлена кафедрой прикладной и теоретической физики
© Новосибирский государственный технический университет, 2006
2
Р А Б О Т А № 40
ОПРЕДЕЛЕНИЕ ШИРИНЫ ЗАПРЕЩЕННОЙ ЗОНЫ ПОЛУПРОВОДНИКА
Ширина запрещенной зоны может быть найдена с помощью измерений электропроводности или постоянной Холла в зависимости от температуры, а также из спектрального распределения фототока полупроводника.
Цель работы
Определить ширину запрещенной зоны полупроводника по температурной зависимости электропроводности. Сравнить полученный результат с табличным.
Зависимость электропроводности от температуры
Электропроводность полупроводника равна сумме собственной и примесной электропроводности:
σ = σi |
+ σпр . |
(1) |
При высоких температурах σi |
>> σпр . Электропроводность собст- |
|
венного полупроводника |
|
|
σi = nieμn + pieμ p , |
(2) |
|
где e – заряд электрона, ni , μn , pi , μ p – концентрации и подвижности электронов и дырок соответственно.
3

E 
0
|
Для того чтобы найти зависимость электро- |
||
|
проводности от температуры, необходимо выяс- |
||
Ε0 |
нить, как изменяются |
концентрации носителей |
|
заряда и их подвижности с изменением темпера- |
|||
|
туры. Рассмотрим чистый полупроводник, не со- |
||
Рис. 1 |
держащий примесей. Пусть ширина его запре- |
||
щенной зоны равна |
E0 . Примем наинизший |
||
|
|||
уровень зоны проводимости за начало отсчета энергии (рис. 1).
Для участия в электрическом токе валентный электрон должен перейти из связанного состояния в валентной зоне в свободное состояние в зоне проводимости. Очевидно, что минимальная энергия, необходимая для такого перехода, равна ширине запрещенной зоны E0 , назы-
ваемой также энергией ионизации атома полупроводника. Эта энергия может быть сообщена электрону за счет теплового движения. Концентрация электронов в зоне проводимости
|
∞ |
|
|
|
∞ |
E −EF |
−1 |
4π(2mn )3 / 2 |
|
|
||
|
|
|
|
|
|
|
||||||
n = |
∫ |
f |
F |
dz = |
∫ |
e kT |
+ 1 |
|
|
E1/ 2dE , |
(3) |
|
|
3 |
|||||||||||
i |
|
|
|
|
h |
|
|
|||||
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где dz – число разрешенных состояний в интервале энергий dE ; fF –
функция Ферми; mn – эффективная масса электрона; EF – энергия
Ферми.
Так как в собственных полупроводниках число электронов, переходящих в зону проводимости, обычно значительно меньше числа состояний в зоне проводимости, то лишь малая часть состояний занята электронами. (Заметим, что число разрешенных энергетических уровней в два раза меньше числа доступных квантовых состояний.) В этом случае функция Ферми переходит в функцию Больцмана:
EF −E |
|
fF = fB = e kT . |
(4) |
Заменяя fF в (3) и интегрируя, получаем
n = |
2 |
(2πm kT )3 / 2 |
|
EF |
|
|
|
|
|
||||
|
n |
e kT . |
(5) |
|||
|
|
|||||
i |
|
h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
Аналогично для концентрации дырок получаем
|
|
|
3 / 2 |
|
|
E0 |
+EF |
|
|
|
|
|
|
|
|
|
|||
pi |
= |
2(2πmp kT ) |
|
e |
− |
kT |
. |
(6) |
|
h3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
В собственном полупроводнике ni = pi . Тогда из (5) и (6) находим
|
|
|
|
|
|
|
3 / 2 |
|
|
|
|
|
|
|
2 2π m m kT |
|
E0 |
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
( |
n p |
) |
|
e− 2kT . |
|
|||
n = |
n p = |
|
(7) |
||||||||
|
|
|
|
|
|||||||
i |
i i |
|
|
h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим зависимость подвижности от температуры. По определению дрейфовая подвижность равна отношению дрейфовой скорости к напряженности электрического поля
μn |
= |
vn |
= |
aτn |
= |
eετn |
= |
eτn |
, |
(8) |
ε |
ε |
mnε |
|
|||||||
|
|
|
|
|
mn |
|
||||
где τn – время свободного пробега электрона (время релаксации). Время релаксации τn равно отношению длины свободного пробега
к скорости теплового движения электрона:
τn = λ vT . |
(9) |
В случае рассеяния носителей заряда на колебаниях решетки (на акустических фононах)
λ = A / T , |
(10) |
||||
|
|
|
|
|
|
vT = |
3kT |
|
|||
|
. |
(11) |
|||
m |
|||||
|
|
n |
|
||
Из (9), (10), (11) получаем выражение для подвижности электронов:
μ |
n |
= |
|
eA |
|
T −3 / 2 |
= BT |
−3 / 2 . |
(12) |
|
|
|
|
||||||||
3km |
||||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
n |
|
|
|
|
|
|
Аналогично для подвижности дырок |
|
|
|
|||||||
|
|
|
|
μ p = CT −3 / 2 . |
|
(13) |
||||
|
|
|
|
|
5 |
|
|
|
||

Из (2), (7), (12), (13) получаем выражение для электропроводности собственного (беспримесного) полупроводника
si = s0e− E0 2kT . |
(14) |
Логарифмируем (14): |
|
ln si = ln s0 - DE0 2kT . |
(15) |
Следовательно, изменение проводимости при изменении температуры определяется из
|
|
DE0 |
|
1 |
|
|
D ln si |
= - |
2k |
D |
|
. |
(16) |
|
||||||
|
|
T |
|
|
||
Ширину запрещенной зоны полупроводника определяем из (16):
|
DE = - |
2kD ln si |
, |
|
(17) |
|||||||
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
D(1/ T ) |
|
|
|||||
|
|
|
|
|
|
|
||||||
где k = 8,6 ×10−5 |
эВ/К, D ln s = ln s |
- ln s = ln s2 , |
|
|||||||||
|
|
i |
|
2 |
1 |
|
s1 |
|
||||
|
|
|
|
|
|
|||||||
|
D(1 T ) =1 T 2 -1 T1 . |
|
|
|||||||||
Значения ln s1 , |
ln s2 , 1 T1 , 1 T2 |
определяются по графику зависимо- |
||||||||||
сти ln s от 1 T . |
|
|
|
|
|
|
|
|
|
|
|
|
Вычисление электропроводности проводится по рабочей формуле |
||||||||||||
|
|
|
si = |
|
I |
|
|
l |
. |
|
(18) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
U34 S |
|
|
||||||
Описание экспериментальной установки
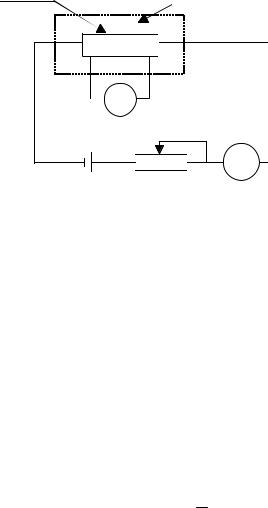
Для определения температурной зависимости электропроводности полупроводника используется принципиальная схема, показанная на рис. 2.
Для определения электропроводности полупроводника измеряются ток и напряжение между контактами 3 и 4. Для снятия температурной характеристики образец помещается в термостат или нагревательную
6
образецОбразец |
рмостат |
|
Термостат |
11 |
2 |
2 |
|
3 |
4 |
V
R
EЕ
mA
Рис. 2
печь. Температура измеряется с помощью термопары либо термометра сопротивления (терморезистора). Чтобы исключить влияние термоЭДС между контактами 3 и 4, измерения проводят при двух противоположных направлениях тока и одной и той же температуре. Значения поперечного сечения образца и расстояния между контактами 3 и 4 приведены в паспорте установки.
Задание к работе
1. Измерить электропроводность σi полупроводникового образца при комнатной температуре.
2.Включить электропечь и измерить зависимость электропроводности σi от температуры образца T .
3.Вычислить среднеквадратичное отклонение электропроводности при комнатной температуре.
4. Построить график зависимости ln σ от 1 .
T
5. Определить ширину запрещенной зоны E0 полупроводника
графически.
6. Сравнить полученный результат с табличным.
7

Контрольные вопросы
1.Какова цель работы?
2.Как вы будете измерять напряжение между контактами 3 и 4?
3.В каких осях вы будете строить график?
4.Как по графику будете определять ширину запрещенной зоны полупроводника?
5.Получите формулу зависимости концентрации носителей заряда
всобственном полупроводнике от температуры.
6. Постройте график зависимости ln σi |
от |
1 |
для случая рассеяния |
|
|||
|
|
T |
|
носителей заряда на акустических фононах.
7. Получите формулу зависимости электропроводности от температуры в случае собственной проводимости.
8. Постройте график зависимости ln n от 1 для области собствен-
T
ной проводимости, области насыщения (истощения) и области вымораживания (области низких температур).
9. Постройте график ln σ от 1 для областей, указанных в п. 8.
T |
|
|
|
10. Как изменяется вид графика ln σ = f |
1 |
|
при увеличении кон- |
|
|||
T |
|
||
центрации примеси?
11.Как объяснить тот факт, что в области насыщения при нагревании образца электропроводность уменьшается?
12.Сравнивая полученное значение ширины запрещенной зоны с табличным значением, сделайте вывод.
ЛИТЕРАТУРА
1.Епифанов Г.И. Физика твердого тела. – М.: Высш. шк., 1996. – Гл. 7,
пп. 2–7.
2.Савельев И.В. Курс общей физики. – М.: Наука, 1982. – Т.3. § 51–55, 57–
59, 1989, § 43.
3. Корнилович А.А. Физика в примерах : Учеб. пособие, Новосибирск: Изд-
во НГТУ, 1994. Гл. 16.
8
РАБОТА № 41
ИЗУЧЕНИЕ ЭФФЕКТА ХОЛЛА, ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ
ИПОДВИЖНОСТИ НОСИТЕЛЕЙ ЗАРЯДА
ВПОЛУПРОВОДНИКЕ
Цель работы
На основании измерений постоянной Холла и электропроводности определить концентрацию и подвижность носителей заряда в полупроводнике. Сравнить полученные результаты с табличными.
Эффект Холла
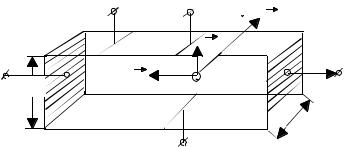
Эффект Холла состоит в следующем. Пусть по полупроводнику, имеющему форму прямоугольной пластины, протекает электрический ток (рис. 1). Контакты: 1, 2 – токовые, 3, 4 – холловские, находящиеся на одной эквипотенциальной поверхности; 3, 5 либо 4, 5 служат для измерения электропроводности.
R
Если образец поместить в однородное магнитное поле B , перпендикулярное направлению тока, то между контактами 3 и 4 возникнет разность потенциалов. Это явление называется эффектом Холла, а по-
перечная разность потенциалов εX – |
ЭДС Холла. |
|
|
5 |
3 |
В |
|
|
|
B |
|
|
F |
|
I |
|
|
2 |
|
v |
|
|
|
-–e |
|
|
|
h 1 |
|
|
|
|
|
d |
|
|
4 |
|
|
Рис. 1 |
|
|
|
9 |
|
|
|

Опыт показывает, что ЭДС Холла пропорциональна индукции магнитного поля B , величине тока I , протекающего через пластину, и обратно пропорциональна ее толщине d :
εX = RIB d . |
(1) |
Коэффициент пропорциональности R называется постоянной Холла.
Рассмотрим механизм появления ЭДС Холла в примесном элек-
тронном полупроводнике. Допустим, |
что все свободные электроны |
||
движутся с одинаковой дрейфовой скоростью v в магнитном поле |
R |
||
B . |
|||
На электроны действует магнитная сила |
|
||
R |
R |
R |
(2) |
FM |
= ev × B . |
||
Под действием этой силы электроны смещаются к верхней грани пластины (рис. 1) так, что между верхней и нижней гранями возникает поперечное холловское электрическое поле EX . Отклонение электро-
нов будет продолжаться до тех пор, пока электрическое поле EX не
уравновесит отклоняющее действие магнитного поля. При этом электрическая сила станет равной магнитной силе:
eEX = evB . |
(3) |
Умножим равенство (3) на число электронов n в единице объема (т.е. на концентрацию электронов):
neEX = nevB . |
(4) |
Известно, что nev есть плотность тока j , равная отношению тока I к сечению образца S = hd . Поэтому
EX |
= |
1 |
|
IB |
. |
(5) |
|
|
|||||
|
|
ne hd |
|
|||
Заменим напряженность холловского электрического поля из соотношения
EX = εX h . |
(6) |
10 |
|
