
- •Министерство образования и науки рф
- •Глава 1. Уровни энергии. Взаимодействие элеКтромагнитного излучения с веществом
- •1.1. Многоэлектронные атомы
- •1.2. Молекулы
- •1.3. Электронные состояния в полупроводниках
- •1.4. Оптические переходы в полупроводниках
- •1.5. Люминесценция
- •1.6. Спонтанное и вынужденное излучение.
- •1.7. Форма и ширина спектральной линии
- •Глава 2. Усиление и генерация
- •2.1. Характеристики неравновесных состояний квантовых систем. Отрицательная температура
- •2.2. Принцип работы квантовых усилителей и генераторов
- •2.3. Возбуждение активного вещества (накачка)
- •2.5. Трехуровневые схемы
- •2.6. Четырехуровневая схема
- •2.7. Оптические резонаторы
- •2.8. Добротность резонатора.
- •2.9. Условие самовозбуждения и насыщение усиления
- •2.10. Свойства лазерного излучения
- •Глава 3. Лазеры
- •3.1. Классификация лазеров
- •3.2. Твердотельные лазеры
- •3.2.1. Рубиновый лазер
- •3.2.2. Лазеры на кристаллах и стеклах,
- •3.3. Жидкостные лазеры
- •3.4. Газовые лазеры
- •3.4.1. Атомарные газовые лазеры
- •3.4.2. Молекулярные лазеры
- •3.4.3. Эксимерные лазеры
- •3.5. Полупроводниковые лазеры.
- •3.5.1. Принцип работы полупроводниковых лазеров
- •3.5.2. Инжекционный лазер на гомопереходе
- •3.5.3. Инжекционный лазер на гетеропереходе
- •3.5.4. Лазеры на квантовых ямах
- •3.5.5. Квантово-какскадные лазеры
- •3.5.6. Полупроводниковые лазеры с электронной накачкой
- •Глава 4. Некогерентные источники
- •4.1. Светодиоды
- •4.2. Спектр излучения светодиодов
- •4.3. Фотоприемники
- •4.4. Фотодиоды
- •Глава 5. Приборы управления световыми
- •5.1. Электрооптические, магнитооптические и пьезооптические эффекты
- •5.2. Оптические модуляторы
- •5.3. Дефлекторы
- •Список литературы
- •Оглавление
- •Глава 1. Уровни энергии. Взаимодействие
- •Глава 2. Усиление и генерация электромагнитного
- •Глава 3. Лазеры . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
- •Глава 4. Некогерентные источники излучения.
- •Глава 5. Приборы управления световыми потоками . . . . . . 97
1.2. Молекулы
В общем случае полная энергия любой молекулы является суммой четырех вкладов:
электронной энергии Ее, определяемой движением электронов вокруг ядер;
колебательной энергии Еv, обусловленной колебаниями ядер;
вращательной энергии Еr, связанной с вращением этой молекулы;
поступательной энергии.
Вклад последний не рассматривается, поскольку он обычно не квантуется. Оценим, используя общие соображения, по порядку величины разность энергий электронных (∆Ее), колебательных (∆Еv) и вращательных (∆Еr) уровней.
Порядок величины ∆Ее определяется из соотношения
![]() ,
(1)
,
(1)
где m - масса электрона, а - характерный размер молекулы.
Для гомоядерной двухатомной молекулы, с атомами массой М, разность энергий ∆Еv между двумя колебательными уровнями определяется соотношением
![]() .
(2) Разность ∆Еr
вращательных
уровней можно выразить через разность
энергий ∆Еv
колебательных уровней
.
(2) Разность ∆Еr
вращательных
уровней можно выразить через разность
энергий ∆Еv
колебательных уровней
![]() .
(3)
.
(3)
Поскольку отношение m/M ≈ 10-4, то расстояния по энергии между вращательными уровнями должны быть приблизительно в сто раз меньше, чем между колебательными. Расстояния между колебательными уровнями, в свою очередь, должны составлять около одной сотой величины ∆Ее.
Согласно квантовомеханическим представлениям, как колебательная, так и вращательная энергия молекулы квантуется.
На
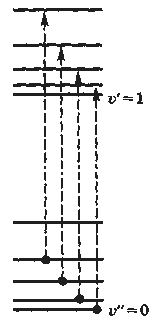
рис. 1.1. показана упрощенная структура
колебательных (а) и вращательных (б)
уровней энергии, принадлежащих двум
последовательным электронным и
колебательным состояния молекулы,
соответственно. Таким образом,
рассматриваемая полная энергия
системы является суммой электронной,
колебательной и вращательной энергий.
Отметим, что в отличие от случая
колебательных уровней, расстояния между
 соседними
вращательными уровнями не являются
по
соседними
вращательными уровнями не являются
по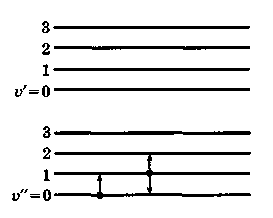 стоянной
величиной.
стоянной
величиной.
(а) (б)
Рис. 1.1. а). Колебательные уровни энергии, относящиеся к двум различным электронным состояниям молекулы. Стрелками показаны разрешенные переходы, начинающиеся с уровней v″=0 и v″=1. б). Вращательные уровни энергии, принадлежащие двум последовательным колебательным состояниям молекулы.
1.3. Электронные состояния в полупроводниках
Энергетическое состояние электронов в идеальном кристалле полупроводникового материала, где атомы расположены в строгом порядке, определяемом кристаллической решеткой, описывается уравнением Шредингера:
![]() ,
(1)
,
(1)
где потенциал взаимодействия U(r) также обладает периодичностью решетки.
Внешние электроны атомов делокализованы по всему кристаллу, а соответствующие волновые функции могут быть записаны в виде волновых функций Блоха:
![]() ,
(2)
,
(2)
где
![]() обладает
теми же свойствами периодичности, что
и кристаллическая решетка,
обладает
теми же свойствами периодичности, что
и кристаллическая решетка,
![]() - волновой вектор плоской волны
- волновой вектор плоской волны![]() .
.
При
подстановке выражения (2) в уравнение
Шредингера оказывается, что получаемые
собственные значения энергии электрона
Е
являются функцией волнового вектора
![]() и
образуют зоны разрешенных значений.
Рассмотрим только наиболее высокую
заполненную зону, называемую валентной
(относящиеся
к ней величины обозначаются индексом
v),
и
следующую, лежащую выше, называемую
зоной
проводимости (соответствующие
величины имеют индекс с).
В
приближении
параболической зоны соотношение
между Е
и
и
образуют зоны разрешенных значений.
Рассмотрим только наиболее высокую
заполненную зону, называемую валентной
(относящиеся
к ней величины обозначаются индексом
v),
и
следующую, лежащую выше, называемую
зоной
проводимости (соответствующие
величины имеют индекс с).
В
приближении
параболической зоны соотношение
между Е
и
![]() имеет
вид параболы. Это приводит к формам
валентной зоны и зоны проводимости,
изображенным на рис. 1.2.
имеет
вид параболы. Это приводит к формам
валентной зоны и зоны проводимости,
изображенным на рис. 1.2.
Действительно, энергия Ес в зоне проводимости, измеренная вверх относительно ее нижнего края, или дна (см. рис. 1.2, а), может быть записана в виде:
![]() ,
(3а)
,
(3а)
где
![]() - так называемая эффективная масса
электрона вблизи дна зоны проводимости.
Аналогично энергияЕv
в
валентной зоне, замеренная вниз
относительно ее верхнего края, или
потолка (см. рис. 1.2, а), может быть записана
в виде:
- так называемая эффективная масса
электрона вблизи дна зоны проводимости.
Аналогично энергияЕv
в
валентной зоне, замеренная вниз
относительно ее верхнего края, или
потолка (см. рис. 1.2, а), может быть записана
в виде:
![]() ,
(3б)
,
(3б)
где
![]() - эффективная масса электрона вблизи
потолка валентной зоны.
- эффективная масса электрона вблизи
потолка валентной зоны.
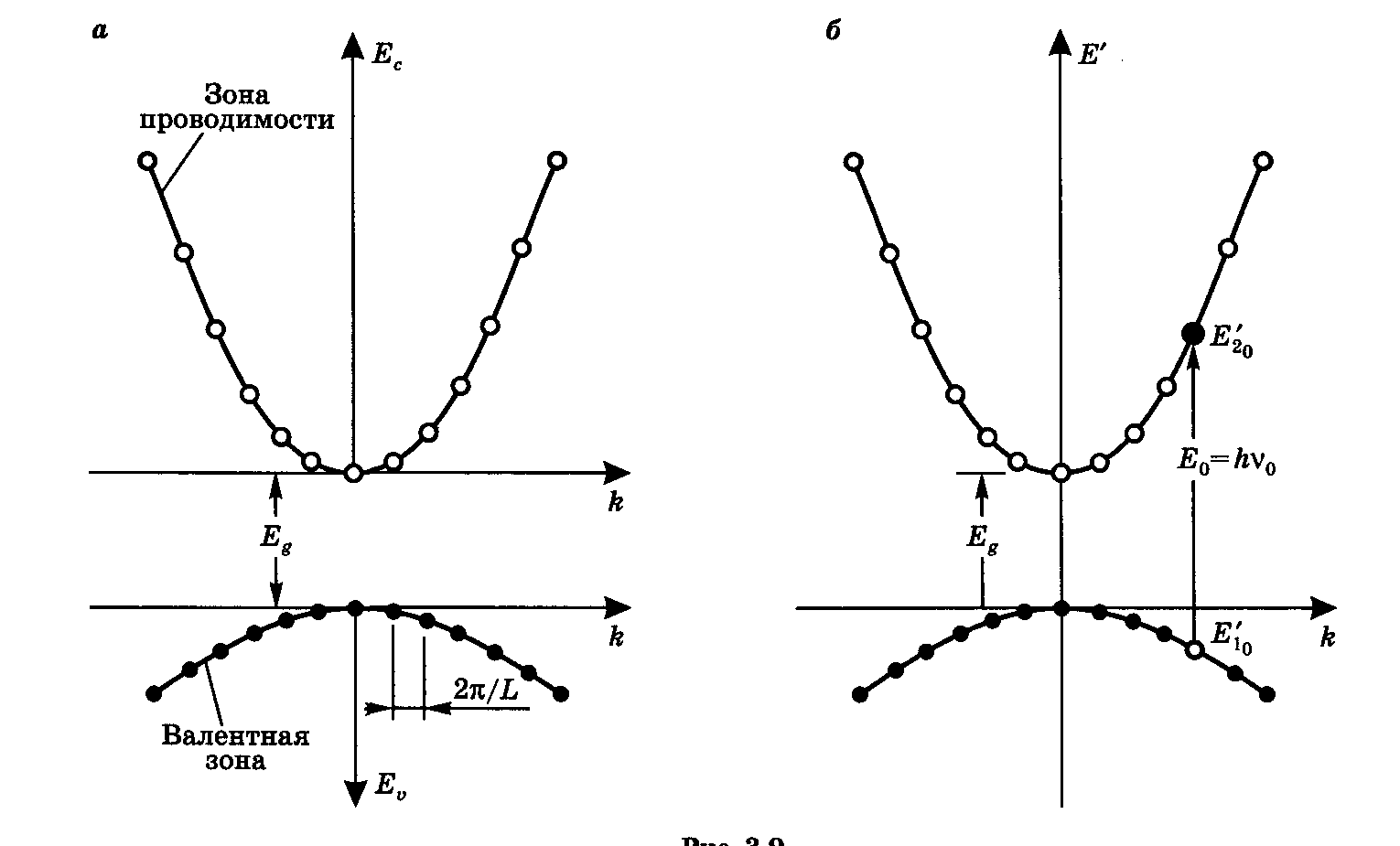
Рис. 1.2. Зависимость Е(k) в объемном полупроводнике: а) положительные отсчеты энергии производятся вверх относительно дна зоны - в зоне проводимости, и вниз относительно потолка зоны - в валентной зоне; б) положительный отсчет энергии производится вверх относительно потолка валентной зоны - как в валентной зоне, так и в зоне проводимости. (Разрешенные состояния в валентной зоне обозначены точками, а в зоне проводимости - окружностями).
В некоторых случаях, особенно когда рассматривается конкретный переход, оказывается более удобным отсчитывать эти энергии в одном направлении и относительно одного и того же уровня, например, вверх относительно потолка валентной зоны (рис. 1.2,6). Если через Е' обозначить энергию в этой системе отсчета, то энергии в зоне проводимости и в валентной зоне будут, очевидно, определяться соотношениями:
Е'с=Еg+Еc, (4а)
Е'v= -Еv, (46)
где Еg - ширина запрещенной зоны, или энергетическая щель.
Эту
простую одномерную модель легко обобщить
на трехмерный случай. Обозначив через
![]() ,
,
![]() и
и
![]() компоненты
волнового вектора электрона
компоненты
волнового вектора электрона
![]() ,
и полагая, что его эффективная масса,
т. е., другими словами, кривизна зоны,
одинакова вдоль направлений х,
у и
z,
опять
получаем соотношения (3) и (4), в которых
теперь k2
= kх2
+ kу2
+
kz2.
,
и полагая, что его эффективная масса,
т. е., другими словами, кривизна зоны,
одинакова вдоль направлений х,
у и
z,
опять
получаем соотношения (3) и (4), в которых
теперь k2
= kх2
+ kу2
+
kz2.
Таким
образом, соотношения (3) и (4) позволяют
достаточно просто описать разрешенные
значения энергий электронов в
полупроводнике в приближении параболической
зоны. Отметим, что в этом приближении
электрон рассматривается как свободная
частица с импульсом
![]() (действительно,
для свободной частицыЕ=р2/2т),
а
свойства полупроводника как реальной
квантовой системы учитываются путем
введения таких параметров, как ширина
запрещенной зоны Еg
и
эффективные массы тс
и
тv..
(действительно,
для свободной частицыЕ=р2/2т),
а
свойства полупроводника как реальной
квантовой системы учитываются путем
введения таких параметров, как ширина
запрещенной зоны Еg
и
эффективные массы тс
и
тv..
