
ФИЗИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОНИКИ
.pdf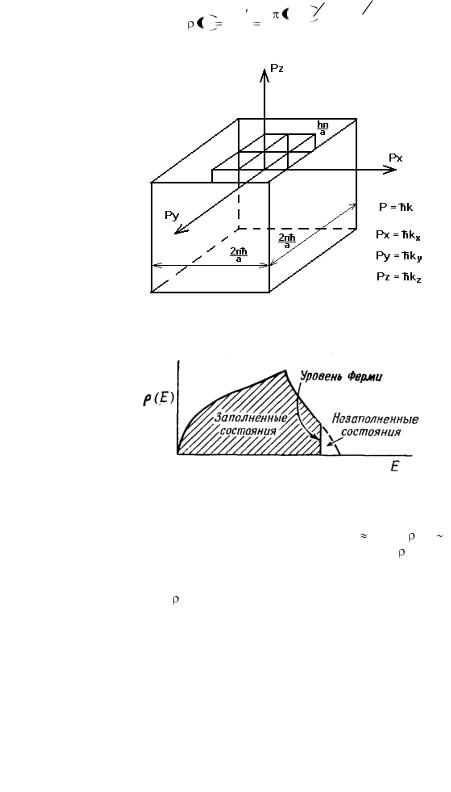
отсюда
E |
dN |
|
4 2m * |
32 gi L3 E |
12 |
. |
(4.49) |
dE |
|
|
h3 |
|
|||
|
|
|
|
|
|
Рис. 4.15. Зона Бриллюэна для простой кубической решетки
Рис. 4.16. Заполнение состояний электронами (твердое тело с почти заполненной зоной)
Вдали от границ зоны Бриллюэна, когда m* const, |
(Е) Е1/2. По |
мере увеличения числа электронов ЕF растет, растет и |
(Е) до тех пор, |
пока сфера Ферми в пространстве импульсов (рис. 4.17) не коснется зоны Бриллюэна.
После чего (Е) будет уменьшаться, при этом сфера Ферми искажается (рис. 4.17).
51
|
|
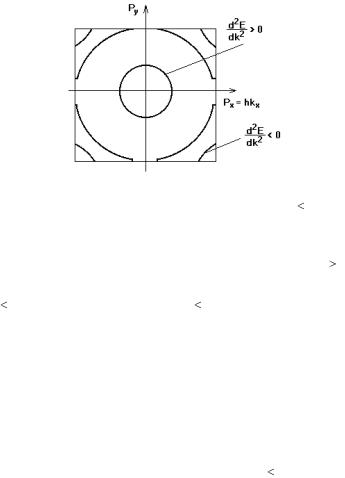
Рис. 4.17. Искажение сферы Ферми при |
d 2 E |
0 |
|
|
|||||
|
|
dk 2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Различают электронные участки сферы Ферми, где |
|
d 2 E |
0 |
и где |
|||||||
|
dk 2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d 2 E |
0 |
(m*>0) и дырочные, где |
d 2 E |
0 |
(m*<0). |
|
|
|
|
|
|
dk 2 |
dk |
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
4.9. Электроны и дырки
Итак, в пространстве импульсов, по мере заполнения электронами импульсного пространства, число состояний увеличивается, увеличивается число состояний и вдали от границ зоны Бриллюэна, сфера Ферми представляет собой сферу и m*>0. При приближении к границам (у потолка зоны Бриллюэна) плотность состояний уменьшается, вид поверх-
ности Ферми изменяется, появляются участки |
d 2 E |
0 . |
||
dk |
2 |
|||
|
|
|||
Такие участки называются дырочными поверхностями Ферми. Электроны ведут себя как фиктивные частицы, обладающие массой и зарядом, противоположными по знаку массе и заряду электрона. Эти частицы называются дырками. Зона, заполненная электронами, не может проводить ток, так как в ней нет свободных состояний. Это относится и к полностью пустой зоне, так как там нет носителей зарядов.
Но проводимость пустой зоны может быть создана путем введения на ее нижние уровни некоторого числа электронов. Поэтому, по аналогии, проводимость в полностью заполненной зоне можно добиться путем удаления некоторого числа электронов с ее верхних уровней. Для этого нужно ввести в рассмотрение фиктивную заряженную частицу,
52
являющуюся зеркальным отражением электрона и обладающую массой и зарядом, противоположным по знаку массе и заряду электрона, находящегося вблизи потока зоны, т.е. дырку. Она заполняет энергетические состояния в заполненной зоне так же, как реальные электроны заполняют энергетические состояния в пустой зоне. Введение группы дырок на верхние уровни зоны эквивалентно образованию почти заполненной зоны, так как дырки аннигилируют с электронами, расположенными вблизи потолка зоны. Дырка представляет собой вакансию электрона, следовательно, ее энергию следует отсчитывать в направлении от потолка зоны вниз. Дырка в середине зоны означает, что кристалл находится в возбужденном состоянии по сравнению с кристаллом, где дырка находится у потолка зоны. Дырка, перемещающаяся вверх (по энергии), соответствует электрону, перемещенному вниз. Эти особенности поверхности Ферми подтверждаются экспериментальными исследованиями.
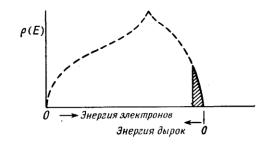
Рис. 4.18. Состояния, занимаемые дырками в почти заполненной зоне
Методы исследования электронных структур
1.Рентгеновские спектры твердых тел.
2.Циклотронный резонанс (метод, позволяющий измерять m*).
3.Эффект де-Гааза – Ван Альфена (в магнитном поле поверхности Ферми).
4.Аномальный скин-эффект.
5.Электронная удельная теплоемкость.
6.Магнитосопротивление кристалла.
53
5. ФИЗИЧЕСКИЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
Класс полупроводников определяют следующие понятия: а) имеют ковалентную связь между атомами.
б) кристаллическая структура типа алмаза.
в) зонная структура (при Т = 0 К): валентная зона (ВЗ) полностью заполнена электронами; зона проводимости (ЗП) полностью свободна; (при Т = 0 К) между ними имеется узкая запрещенная зона Еg.
5.1. Собственные полупроводники (электроны и дырки)
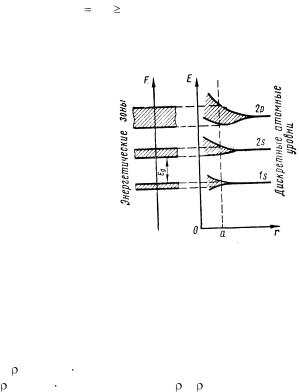
Химически чистые полупроводники называются собственными полупроводниками. К ним относятся чистые элементы (Ge, Si, Sn, и др.) и многие химические соединения (GaAs, InAs, InSb и др., на молекулу GaAs приходится 8 валентных электронов, образующих ковалентную связь). Для них (при T = 0 K) далее будет показана зонная структура. C повышением температуры до величины, при которой тепловая энергия электронов E kT E g , электроны переходят из ВЗ в ЗП. Это приво-
дит к появлению в ЗП свободных электронов, а в ВЗ свободных уровней, на которые могут переходить другие электроны этой зоны.
Рис. 5.1. Расщепление дискретных атомных уровней
Если приложить к такому кристаллу электрическое поле Е, то в нем возникает движение электронов в ЗП и ВЗ, приводящее к появлению электрического тока. Кристалл становится проводящим. Чем уже Еg и больше Т, тем больше электронов в ЗП, тем большая проводимость. Так, у Ge Еg=0,66 эВ и при Т=293 К концентрация электронов n=1019 м-3 и =0.48 Ом м. Для сравнения: у алмаза Еg=5,2 эВ (Т=293 К) и n=104 м-3,
=108 Ом м, но при Т=600 К и C= Ge (при Т=293 К).
54
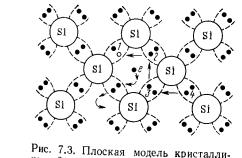
Итак, проводимость полупроводников является проводимостью возбужденной. Она появляется под действием внешних факторов: нагревания, облучения светом и ионизированного излучения.
5.1.1. Дырочные примеси в полупроводниках
Рассмотрим более подробно поведение электронов в ВЗ, в которой возникают свободные уровни вследствие перехода части электронов в ЗП. Эти свободные состояния у потолка ВЗ, как мы рассмотрели в предыдущей теме, эквивалентны зарядам +e с массой mр, численно равной отрицательной массе электрона mn, ранее занимавшего данное состояние вблизи потолка ВЗ. Поэтому ток, создаваемый дырками, будет совпадать как по величине, так и по направлению с током, созданным электронами, почти полностью заполненной ВЗ. На языке ковалентной связи: электрон, перешедший в ЗП – аналогично тому, что атом потерял одну связь, появилась дырка, т.е. при внешнем возбуждении (теплота, облучение) произошла генерация (рис. 5.2) – образовались свободные электрон и дырка.
Рис. 5.2. Процессы генерации и рекомбинации носителей заряда в собственном полупроводнике
Место дырки 1 и 2 может быть занято электронами 3 и 4. Следовательно, дырки 1 и 2 переходят в места 3 и 4, и т. д. В электрическом поле электроны движутся против поля Е, а дырки – вдоль поля Е. Но так как заряд у них разного знака, то токи их складываются. Вследствие теплового движения электрон из ЗП может встретиться с дыркой и происходит процесс, обратный генерации, т.е. исчезает свободный электрон
идырка – это процесс рекомбинации.
5.2.Примесные полупроводники (донорные и акцепторные)
Полупроводники любой степени чистоты всегда содержат примесные атомы, создающие свои энергетические уровни, получившие название примесных уровней. Эти уровни могут располагаться как в разре-
55
шенных, так и в запрещенных зонах. В ряде случаев примеси вводят сознательно для придания полупроводнику необходимых свойств. Рассмотрим типы примесных уровней.
5.2.1. Донорные уровни
Эти уровни создаются примесями атомов, имеющими валентность выше валентности чистого полупроводника. Так, если в решетке Ge (валентность – 4) вводится As (валентность – 5), для установления связей As отдает 4 электрона, 5-й электрон в образовании связей не участвует
(рис. 5.3).
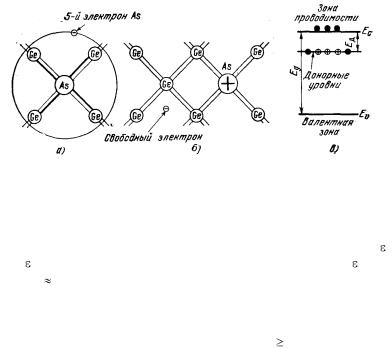
Рис. 5.3. Примесный полупроводник n-типа: а) и б) появление свободного электрона,
в) энергетический донорный уровень
Он продолжает оставаться в поле атома As, ослабленного в Ge в = 16 раз ( Ge=16), а энергия его связи с атомом As уменьшается в 2 = 256 раз, т.е. ЕД 0,01 эВ, при такой энергии он отрывается от атома As, превращаясь в электрон проводимости. На языке зонной теории: между заполненной ВЗ и свободной ЗП располагаются энергетические уровни пятого элемента As. Эти уровни размещаются около дна ЗП на расстоянии ЕД. При сообщении таким электронам энергии ЕД они переходят в ЗП. Образующиеся при этом дырки локализуются у атома As и в проводимости не участвуют. Таким образом, примеси, являющиеся источником электронов в проводимости, называются донорными, а их уровни – донорными уровнями. Полупроводники с донорными примесями называются донорными полупроводниками или полупроводниками n-типа.
5.2.2. Акцепторные примеси
Уровни, создаваемые примесями атомов, валентность которых ниже валентности основного полупроводника, называются акцепторными
56
уровнями. Так если в кристалл Ge ввести примеси In (3-валентного), для образования связи с четырьмя ближайшими соседями Ge, у атома In не хватает одного электрона (рис. 5.4). Такая дефектная связь представляет собой дырку. При Т > 0 К это место может занять любой соседний электрон, для этого нужно ему сообщить Еа 0,01 эВ (Еа = акт).
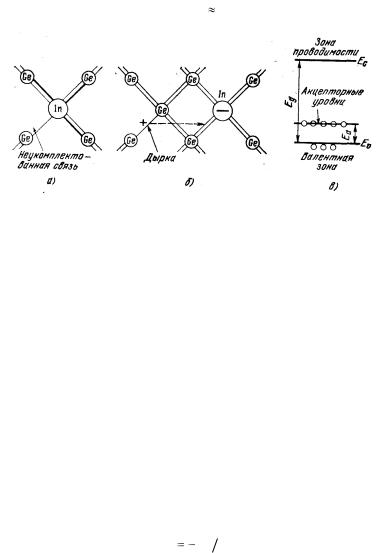
Рис. 5.4. Примесный полупроводник р-типа:
а) и б) появление дырки; в) энергетический акцепторный уровень
На языке зонной теории это означает: вблизи потолка ВЗ на расстоянии Еа появляются свободные уровни. Это приводит к тому, что при относительно невысоких температурах электроны из ВЗ переходят на примесные уровни. Связываясь со свободными связями, они в электропроводности не участвуют, а появившиеся в ВЗ дырки становятся носителями положительного заряда и создают электропроводность. Итак, примеси, захватывающие электроны из ВЗ полупроводника, называются акцепторными, а энергетические уровни этих примесей – акцепторными уровнями. Полупроводники, содержащие такие примеси, называются дырочными, или полупроводниками р-типа.
5.3.Положение уровня Ферми и концентрация носителей
вполупроводниках
5.3.1. Собственные полупроводники
Если обозначить концентрацию электронов – n, а дырок – р, то для собственных полупроводников n=р, так как число дырок в ВЗ равно числу электронов в ЗП. Как показывают расчеты, при Т=0 К энергия Ферми
E F E g 2 , |
(5.1) |
т.е. уровень Ферми располагается посередине ЗЗ. При повышении Т он смещается вверх к дну ЗП, если mp>mn, и вниз к потолку ВЗ, если mp<mn
(рис. 5.5).
57
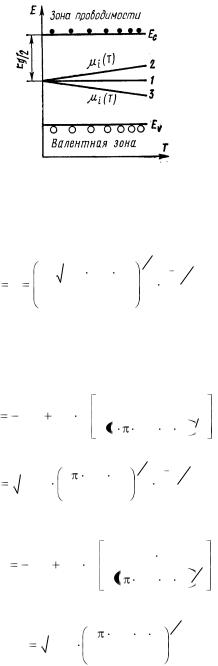
Рис. 5.5. Положение уровня Ферми в собственном полупроводнике:
1 – Т=0 К; 2 – Т>0 К, mp>mn; 3 – Т>0 К, mp<mn
Однако это смещение незначительно, и им обычно пренебрегают. Расчет дает:
|
|
|
|
|
|
3 |
2 |
|
|
|
|
2n m |
|
m |
|
Eq |
|
||||
|
p |
n |
kT |
|
|
|||||
n p |
|
|
|
|
|
|
e 2kT , |
(5.2) |
||
|
|
|
|
|
|
|
||||
|
h 2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
т.е. n = f (Еg,Т), а также и для р.
5.3.2. Примесные полупроводники
Электронный полупроводник
Ef |
EД |
|
kT |
ln |
NД h3 |
, |
|
2 |
2 |
2 2 mn k T 3 2 |
|||||
|
|
|
|||||
где NД – концентрация донорских примесей и
|
|
|
|
2 mn kT |
3 |
2 |
EД |
|
|
|
|
|
|||
n 2N |
|
|
|
|
e kT . |
||
Д |
|
h 2 |
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Дырочный полупроводник
E F |
Ea |
|
kT |
ln |
|
Na |
h3 |
|
, |
|
2 |
2 |
|
|
|
|
3 |
||||
|
2 2 |
m |
p |
k T 2 |
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
где Na – концентрация акцепторной примеси и
|
|
2 |
mp |
k T |
3 |
2 |
|
|
|
|
. |
||||
p 2Na |
|
|
|
|
|||
|
h 2 |
|
|
||||
|
|
|
|
|
|
|
|
58 |
|
|
|
|
|||
(5.3)
(5.4)
(5.5)
(5.6)
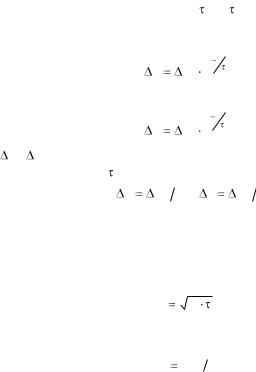
5.4. Неравновесные носители заряда
При Т > 0 К идут процессы генерации свободных носителей заряда. Если бы этот процесс был единственным, то концентрация носителей возрастала бы со временем. Однако, наряду с этим, возникает процесс рекомбинации свободных носителей. Он состоит в том, что свободные электроны при встрече с дыркой занимают ее место, и пара исчезает. При любой Т между генерацией и рекомбинацией устанавливается равновесие, которому соответствует равновесная концентрация носителей. Такие носители называются равновесными. Помимо теплового возбуждения, генерация носителей может происходить под действием света, ионизации, инжекции носителей через контакт. Это приводит к появлению дополнительных носителей, которые называются неравновесными. Каждый неравновесный носитель, возникнув в полупроводнике, живет ограниченное время, до рекомбинации. Поэтому вводят понятия времени жизни носителей: n и p электронов и дырок. Как показывает теория, концентрация избыточных носителей через время t после выключения возбужденной генерации (например света) равна
|
|
|
t |
|
n |
n0 |
e |
n |
(5.7) |
|
||||
и |
|
|
|
|
|
|
|
t |
|
p |
p0 |
e p , |
(5.8) |
|
где n0, p0 – концентрация электронов и |
дырок к моменту выключения |
||
возбуждения. Если t = , то из (5.7) и (5.8) |
следует: |
|
|
n |
n 0 e и p |
p0 e . |
(5.9) |
Таким образом, среднее время жизни избыточных носителей равно времени, в течение которого их концентрация уменьшается в е раз. Свободные носители заряда диффундируют в объеме полупроводника за время своей жизни на расстояние L, которое называется диффузионной длиной носителей. Расчеты дают:
L D , |
(5.10) |
где D – коэффициент диффузии носителей, связанный с их подвижностью u соотношением Эйнштейна:
D kTu q . |
(5.11) |
Процесс перехода из ЗП в ВЗ может происходить через всю запрещенную зону Еg (межзонный переход) или на примесный уровень Еn, а затем с него в ВЗ – рекомбинация в примесный уровень (рис. 5.6).
59

Рис. 5.6. Схема межзонной рекомбинации (1) и рекомбинации через локальный уровень (2 и 3)
При обоих типах рекомбинаций выделяется одна и та же энергия Еg, но в первом энергия выделяется сразу (1), а во втором – по частям
(2) и (3). Выделенная энергия может происходить или в виде кванта h или в виде тепла (фононов). В первом случае рекомбинацию называют
излучательной, а во втором безизлучательной. Как показывает расчет и опыт, межзонная излучательная рекомбинация может иметь место для полупроводника с узкой ЗЗ при комнатной температуре и выше. В случае широкой ЗЗ основной механизм – безизлучательный. Для арсенида галия GaAs доля излучательной рекомбинации может достигать 50% от общего числа рекомбинаций, поэтому он является основным материалом для светодиодов и источников когерентного излучения (полупроводниковых лазеров).
5.5. Собственная проводимость полупроводников
Полупроводники высокой степени очистки (1атом на 108-109атомов полупроводника) в области не слишком высоких температур обладают электрической проводимостью, обусловленной собственными носителями n и p. Эту проводимость называют собственной проводимостью полупроводника. Удельная электропроводность определяется из проводимости электронов n = un ni q и дырок p = up pi q, где un и up – подвижность электронов и дырок.
un = vn / E,
где vn = qE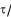 mn – скорость дрейфа; Е – напряженность электрического поля (аналогично для дырок). Так как n = p, то полная проводимость
mn – скорость дрейфа; Е – напряженность электрического поля (аналогично для дырок). Так как n = p, то полная проводимость
= n+ p=q n (un+up). |
(5.12) |
60
