основы твёр-го тела

меньше электронов способно преодолеть ее. Высота потенциального барьера соответствует ширине запрещенной зоны. По ширине запрещенной зоны можно провести классификацию твердых тел на металлы, диэлектрики и полупроводники. Если ширина запрещенной зоны Eg > 2 ÷3 эВ, то твердое тело называется диэлектриком. При

абсолютном нуле температуры диэлектрик имеет полностью заполненную валентную зону и пустую зону проводимости. В случае, когда валентная зона заполнена частично, или наблюдается перекрытие зон, при этом запрещенная зона отсутствует Eg → 0 , такое твердое тело

является металлом. Промежуточное положение занимают полупроводники. Различие между полупроводниками и диэлектриками чисто условное. Можно сказать, что полупроводники – это диэлектрики с Eg < 2 эВ, у которых при низкой температуре все состояния в

валентной зоне заполнены электронами.

2.2. Приближение слабой связи.

а. Свободный электронный газ в металлах.

Для описания поведения электронов в твердом теле в рамках классической электронной теории металлов Друде – Лоренца используют понятие свободного электронного газа, когда каждый атом металла отдает в общее пользование по одному валентному электрону. Эти свободные электроны подобны идеальному газу

20

невзаимодействующих и не имеющих размеров молекул из молекулярной физики. При этом кулоновское отталкивание всеми другими электронами металла уравновешивается притяжением ядрами (ионами) атомов. Свободные электроны участвуют в хаотическом (тепловом) движении и сталкиваются с ионами кристаллической решетки, что приводит к установлению теплового равновесия между электронным газом и кристаллической решеткой. При этом средняя скорость теплового движения электронов аналогична средней скорости молекул идеального газа. Таким образом, рассматривать электронный газ по аналогии с идеальным возможно только при выполнении условий термодинамического равновесия.

Если электрон движется со скоростью υ, то его импульс

Эта формула выражает зависимость кинетической энергии от волнового числа, которая называется дисперсионной зависимостью (законом дисперсии). Для свободного электрона закон дисперсии квадратичен. Но движение электрона в кристалле нельзя считать свободным. Электрон в этом случае будет являться квазичастицей, обладающей определенными значениями основных параметров –

квазиимпульса, квазиволнового числа и эффективной массой,

отличающейся от массы покоя электрона.

б. Периодичность кристалла. Функция Блоха. Граничные условия Кармана-Борна. Зоны Бриллюэна.

В рамках приближения слабой связи описывают состояние квазисвободного электрона, движущегося в периодическом поле кристаллической решетки. Так как идеальном кристалле атомы расположены в узлах кристаллической решетки, образуя строго периодическую структуру, то потенциальная энергия электрона V (r)

также зависит от пространственных координат, т.е. обладает трансляционной симметрией:

21

где r – радиус-вектор электрона, ai (i =1,2,3) - векторы трансляций.

Решением уравнения Шредингера (2.0) в случае периодического потенциального поля является функция Блоха ψk (r)

где A – нормировочный множитель. Волновая функция (2.4а) описывает движение свободного электрона с импульсом (2.1) и энергией (2.2). Рассмотрим подробнее граничные условия для решения уравнения Шредингера, связанные с периодичностью расположения атомов в кристаллической решетке. Пусть кристалл имеет форму параллелепипеда с размерами Lx , Ly , Lz по осям x, y, z соответственно.

Для кубической решетки с периодом a

где Nx, N y , Nz – число атомов на соответствующих ребрах кристалла. Следствием периодичности расположения атомов в кристалле для

22

Таким образом, компоненты волнового вектора kr изменяются дискретноr , следовательно, дискретно меняются компоненты импульса pr = hk , и в соответствии с этим энергия электронов в разрешенной зоне

оказывается квантованной.

Из формул (2.5), (2.9) можно получить пределы изменения k

состояний, соответствующих различным значениям k , т.е. равное числу атомов в кристалле. Учет принципа Паули позволяет заключить, что в разрешенной зоне может находиться 2N квантовых состояний, что подтверждает сделанное ранее предположение. Если аналогично обычному пространству координат (x, y, z) рассматривать пространство

квазиволновых векторов ( kx , ky, kz ) или пространство квазиимпульсов

( px , py, pz ), то из формул (2.10) – (2.12) видно, что эти пространства

являются обратными по отношению к пространству координат. Значениям квазиволнового вектора (квазиимпульса) в интервалах, определяемых формулами (2.10) – (2.12) в пространстве квазиволнового вектора (квазиимпульса) соответствует некоторая область, называемая первой зоной Бриллюэна. Первая зона Бриллюэна является ячейкой Вигнера – Зейца в обратном пространстве. Принцип ее построения рассмотрен в параграфе 1.1. На рисунке 1.3 приведена первая зона Бриллюэна для типичных полупроводников – кремния и германия.

Вторая (следующая) зона Бриллюэна состоит из двух участков: от π a до

зоны Бриллюэна. Каждая зона Бриллюэна содержит все возможные значения квазиимпульса. Все зоны Бриллюэна дают состояния,

23

физически эквивалентные состояниям первой зоны Бриллюэна, и всю зонную схему кристалла можно представить в пределах одной — приведенной зоны Бриллюэна (рис. 2.3).

В приведенной зоне Бриллюэна используются преимущественно две верхние разрешенные зоны – валентная зона и зона проводимости,

имеет решения не при всех значениях энергии. Области разрешенных энергий чередуются с зонами запрещенных энергий. В модели слабой связи это объясняется брэгговским отражением электронных волн в кристалле. Рассмотрим этот вопрос подробнее. Пусть электронная волна отражается от системы кристаллических плоскоcтей, перпендикулярныхr r

вектору обратной решетки G , в обратном направлении k0 = −k1 .

24

Эта функция описывает скопление отрицательного заряда на положительных ионах, где потенциальная энергия E1 – наименьшая. Аналогично, из формулы (2.16а) получаем:

Эта функция описывает такое распределение электронов, при котором они располагаются преимущественно в областях, соответствующих серединам расстояний между ионами. При этом потенциальная энергия E2 будет больше. Функции ψ2 будет соответствовать энергия E2 > E1 .

Таким образом, одному и тому же значению k на границе зон

границу первой зоны, а энергия E2 – нижнюю границу второй зоны.

Это означает, что при распространении электронных волн в кристаллах возникают области значений энергии, для которых не существует решений уравнения Шредингера, имеющих волновой характер. Таким образом, приближение свободных электронов, как и приближение

25

сильной связи, приводит к возникновению разрешенных и запрещенных энергетических зон.

в. Обоснование использования приближения слабой связи.

Рассмотрим, насколько оправдано описанное приближение. Как известно из квантовойr механики, движение свободного электрона с волновым вектором k можно описать с помощью волнового пакета, представляющего собой суперпозицию плоских волн с непрерывно меняющимися значениями k в пределах от k − k до k + k

k − k

Движение волнового пакета характеризуется групповой скоростью

υгр = ddkω , равной скорости перемещения, например, его максимума.

Найдем координату максимума из условия x − ddkω t = 0:

Следовательно, скорость движения электрона равна групповой скорости волнового пакета. Мы получили, что движение электрона в кристалле описывается волновой функцией (2.4), которая является набором волновых функций с разными значениями k . Таким образом, движение электрона в кристалле можно описать волновым пакетом, составленным из блоховских волновых функций, групповая скорость которого равна средней скорости движения электрона в кристалле. Этот важный вывод придает квантовомеханический смысл методу эффективной массы, рассмотренному далее.

г. Эффективная масса электрона в кристалле.

Движение свободного электрона под действием внешней силы F подчиняется второму закону Ньютона, однако особенности движения электронов в кристалле обусловлены их взаимодействием с кристаллической решеткой. Поведение отдельного электрона в кристалле может быть описано тем же уравнением, что и для свободной

26

то уравнение (2.27) есть закон Ньютона, связывающий внешнюю силу, массу и ускорение. Для свободных электронов формула (2.28) с учетом

(2.2) дает m* = m .

Рассмотрим рис. 2.4. Вблизи дна разрешенной зоны знак второй производной d 2 E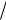dk 2 положителен, следовательно, эффективная масса

электрона m* > 0 и по порядку величины сравнима с массой свободного электрона. Но около средней части разрешенной зоны наблюдается перегиб кривой E(k) , так что d 2 Edk 2 обращается в нуль, а величина

m* → ∞. Потом эффективная масса меняет знак и становится величиной

27

отрицательной. Это можно понять, если вместо электрона рассматривать дырку (вакансию электрона), имеющую положительные эффективную массу и элементарный заряд, но движущуюся в противоположном электрону направлении. Из рисунка 2.4 видно, что вблизи точек экстремума кривая E(k) практически выходит на горизонталь, а в

учетом формулы (2.22) скорость электронов на границах зоны Бриллюэна равна нулю. Это соответствует брэгговскому отражению электронных волн в кристалле.

В общем случае эффективная масса электрона является тензором второго ранга

Эффективная масса электрона, движущегося в определенном кристаллографическом направлении, зависит от направления движения электрона в кристалле и определяется через конкретную компоненту тензора (2.29). Экспериментальное определение эффективной массы электрона при движении в различных кристаллографических направлениях в кристалле производится разными методами, например, оптическими, при исследованиях термоэлектрических и гальваномагнитных явлений, с помощью эффекта поля или с использованием циклотронного резонанса.

d. Механическая аналогия эффективной массы.

В качестве механической аналогии эффективной массы электрона можно рассмотреть эффективную массу твердого шарика, находящегося в жидкости, плотность которой возрастает сверху вниз. Рассмотрим движение шарика массой m в сосуде, заполненном двумя жидкостями различной плотности (рис.2.6). Пусть плотность жидкости меняется от

28

Следовательно, эффективная масса шарика определяет действие на него внутренней силы FA и изменяется аналогично эффективной массе

электрона. При ρ > ρж , то есть в верхней части сосуда, m* > 0, в средней части m → ±∞, а в нижней части, где ρ < ρж , m* < 0 .

29