Коефіцієнт парної кореляції

Коефіцієнт парної кореляції обчислюється за формулою:

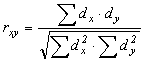або

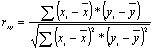
Алгоритм розрахунку коефіцієнта парної кореляції:

1) записують вихідні дані в два варіаційні ряди - x і y;

2) обчислюють середнє арифметичне ряду x і y;

3) визначають різницю між членом ряду і середніми величинами;

4) перемножують різниці ряду x і y між собою;

5) знаходять суму перемножуваних різниць (з урахуванням арифметичного знаку);

6) зводять квадрат кожної різниці (відхилення) ряду х і у;

7) визначають суму квадратів відхилень (різниць) для ряду х і окремо;

8) підставляють отримані дані у вихідну формулу і обчислюють коефіцієнт парної кореляції.

Приклад. Визначити кореляційний зв'язок між рядками введення протидифтерійної сироватки та летальністю цього захворювання.

День введення сироватки (х)	Летальність (у)	d x	d y	d x2	d y2	d x* dx
1-й	2,0	-2	-5	4	25	10
2-й	3,0	-1	-4	1	16	4
Третя	7,0	0	0	0	0	0
4-й	9,0	+1	+2	1	4	2
5-й	14,0	+2	+7	4	49	14
xx = 3	x y= 7.0	Sd x= 0	Sd y= 0	Sd x2= 10	Sd y2= 94	Sd x* dy= 30

Коефіцієнт кореляції дорівнює +0,98. Зв'язок позитивна, сильна. Отже, між термінами введення сироватки та летальністю від дифтерії є дуже тісна залежність. Число хворих у цьому прикладі дорівнює 900.

Можна визначити достовірність коефіцієнта кореляції, обчисливши його середню помилку для великого числа спостережень (n> 50) за формулою:

, Або при меншій кількості спостережень:

З достатньо великою надійністю можна стверджувати, що залежність невипадкова, якщо чисельне значення r xy перевищує свою середню помилку не менш ніж в 3 рази.

Тобто зв'язок між ознаками вважається статистично значущим, якщо коефіцієнт кореляції перевищує свою помилку в 3 і більше разів.

У тому випадку, коли відношення коефіцієнта кореляції до його середньої помилки менше 3, існування зв'язку між досліджуваними явищами не можна визнати доведеним.

Для малої кількості спостережень (n £ 30) ступінь надійності коефіцієнта кореляції може визначатися за спеціальною таблицею. При цьому число спостережень таблиці К (число ступенів свободи n ) дорівнює кількості спостережень у дослідженні без двох, тобто К = n-2. Як правило, коефіцієнт кореляції розраховується при числі кореляційних пар не менше 5.

У медичних і біологічних дослідженнях зв'язок між ознаками вважається статистично значущим, якщо величина коефіцієнта кореляції більше або дорівнює табличній при Р = 0,05

Показники оцінки коефіцієнта кореляції при малому числі спостережень

K	P
	0,1	0,05	0,02	0,01
1	0,988	0,997	0,9995	0,99988
2	900	950	980	990
3	800	878	934	959
4	729	811	882	917
5	669	754	883	874
6	662	707	789	834
7	582	666	750	798
8	549	632	716	765
9	521	602	685	735
10	497	576	658	708
11	476	532	634	684
12	458	532	612	661
13	441	514	592	641
14	426	497	574	623
15	412	482	558	606
16	400	468	542	590
17	389	456	528	575
18	378	444	516	561
19	369	433	503	549
20	360	423	492	537
25	323	381	445	487
30	296	349	409	449
35	275	325	381	418
40	257	304	358	393
45	243	288	338	354
50	231	273	322	354
60	211	250	295	325
70	195	232	274	302
80	183	217	256	283
90	173	205	242	267
100	164	195	230	254

Приклад. У районах вивчалася залежність між щепленнями населення і рівнем захворюваності. Отриманий коефіцієнт кореляції за цими двома ознаками дорівнював 0,81. Число спостережень - 8 районів (пар), отже, К дорівнює 6 (8-2). По таблиці знаходимо рядок 6 і порівнюємо отриманий коефіцієнт. При даному числі ступенів свободи (К) коефіцієнт кореляції перевищує табличний для ймовірності Р = 0,05 (графа 3). Звідси з ймовірністю, більшою, ніж 95%, можна стверджувати, що залежність між щепленнями населення і захворюваністю не випадкова, і цей зв'язок сильна, тобто чим більше відсоток щеплених, тим менше рівень захворюваності.