4.8.5. Решение нелинейного уравнения

Решение уравнений средствами Excel является одним из полезных прикладных применений для инженерных задач. Пусть задано следующее квадратное уравнение: 2х² + 3х – 9 = 0, для определения корней которого необходимо выполнить следующее. Решение уравнения будем формировать в одной из ячеек листа Excel, например в В1, в которую введем искомое значение корня х=0. Исходное уравнение запишем в виде формулы в ячейку В2 (рис.4.42). Для получения решения уравнения вызовем средство Excel Подбор параметра, которое является частью блока задач, иногда называемым инструментом анализа «что-если». Под данным анализом понимают процесс изменения значений ячеек и последующий анализ влияния данных изменений на результат вычисления формулы.

Вызов средства Подбор параметра осуществляется из меню Сервис (рис.4.42).

Рис.4.42. Окно Подбор параметра

Для подбора определяемого параметра Excel в одной конкретной ячейке изменяет значение (в нашем примере это ячейка В1) до тех пор, пока формула, зависимая от этой ячейки, не возвращает требуемый результат, то есть 0 для рассматриваемого примера (рис.4.43).

Рис.4.43. Решение уравнения методом подбора результата

В результате решения уравнения Excel сформировал вместо точного результата х=1,5 приближенный результат х=1,499996529, что связано с использованием интерактивных приближенных методов вычислительной математики, полученная погрешность <0,00001. В качестве начального значения в ячейке В1 можно ввести и другое, например 0. Попробуйте самостоятельно рассмотреть и другие варианты.

4.8.6. Решение системы уравнений

Рассмотрим в качестве примера решение системы нелинейных уравнений с двумя неизвестными в ограниченных пределах изменения переменной Х, что часто требуется в экономических задачах:

У=Х² +2;

Z=3/Х +2.

Решением системы уравнений будет являться точка пересечения двух функций У=F(X) и Z=F(X), а точность определяется выбранным шагом дискретизации переменной Х, переменная Х задана в интервале Х=(0,1-2) с шагом ∆Х=0,1 (рис.4.44).

Рис.4.44. Решение системы уравнений

Для построения данных функций в столбце А заданы значения переменной Х, в ячейках В2:В21введены формулы для вычисления функции У= Х² +2, а в ячейках С2:С21 - формулы для вычисления функции Z=3/Х +2. Решением системы уравнений является значение Х= 1,44 на пересечении графиков функций У и Z. Как видно из графиков, более точное решение можно получить при использовании шага ∆Х=0,05.

4.8.7. Численное интегрирование функций

Вначале остановимся кратко на понятии определенный интеграл. Пусть на отрезке [a, b] задана функция y =f(х), и отрезок [a, b] разбит на n элементарных отрезков в точках х₀., х₁,..., х_n.: а = х₀<х₁<х₂<...<х_п = b.

На каждом отрезке разбиения [x_i-1., x_i] выбрана некоторая точка ζ_i и положено, что ∆x_i = x_i - x_i-1, где i = 1, 2, ..., п. Тогда сумму вида:

называют интегральной суммой функции y =f(х) на [a, b]. Данная интегральная сумма определяется как способом разбиения отрезка [a, b], так и выбором точек ζ₁, ζ₂,... ζ_n = 0 на каждом из отрезков разбиения ∆x_i = x_i – x_i-1, i = 1, 2, ..., n. Обозначим через max ∆x_i максимальную из длин отрезков [x_i-1, x_i], где i = 1, 2, ..., n.

Тогда определенным интегралом от функции y =f(х) на [a, b] называют предел интегральной суммы при стремлении max x_i, к нулю, если он существует, конечен и не зависит от способа выбора точек х₁, х₂,. и точек ζ₁ ζ₂. Определенный интеграл обозначается как:

а f(x) называют интегрируемой в пределах [a, b], то есть:

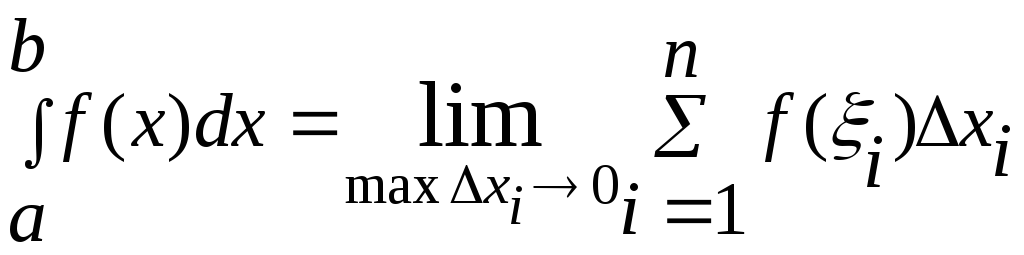
Число а называют нижним пределом определенного интеграла, число b - его верхним пределом.

Геометрический смысл определенного интеграла заключается в следующем. Если функция y =f(х) неотрицательна на отрезке [a, b], где а < b, то численно равен площадиS под кривой у =f(x) на [a, b] .

Действительно, отдельное слагаемое интегральной суммы (1) равно площади S_i прямоугольника со сторонами ∆x_i и f(x.) (согласно определению значение определенного интеграла не зависит от способа выбора точек ζ₁, ζ₂,...), где i= 1, 2,... n (рис. 4.45). Поэтому вся интегральная сумма (1) равна площади S_i = S_i+S₂+...+S_n под ломаной, образованной на каждом из отрезков [x_i-1, x_i] прямыми, параллельными оси абсцисс. При стремлении max ∆x_i к нулю ломаная неограниченно приближается к исходной кривой, а площадь под ломаной переходит в площадь под кривой S_i = S.

Рис. 4.45. Графическая интерпретация определенного интеграла

В экономических приложениях определенный интеграл может выражать, например, объем произведенной продукции (и) при известной функции производительности труда f(t):

.

Обычно для нахождения определенного интеграла используется формула Ньютона-Лейбница:

.

Однако применение формулы (3) на практике связано с существенными трудностями, возникающими при нахождении первообразной в случае усложнения подынтегральной функции. Поэтому в приложениях используют так называемые численные методы, позволяющие найти приближенное значение искомого интеграла с требуемой точностью. Этот подход оказывается особенно предпочтительным при использовании компьютеров для нахождения интегралов.

Существует значительное количество численных методов вычисления интегралов. Они основаны на разных способах нахождения площади под кривой f(х):

как суммы элементарных трапеций - метод трапеций:

,как суммы элементарных прямоугольников - метод прямоугольников:

.

Существуют также метод Симпсона и ряд других.

Формула метода прямоугольников (4) получается, если отрезок интегрирования [a, b] разбить на п равных частей длиной:

На каждом из отрезков разбиения [x_i-1, x_i] участок кривой у=f(x) заменяется отрезком прямой, параллельным оси абсцисс. Тогда:

,где S₁, S₂,..., S_n - площади прямоугольников на каждом из отрезков разбиения. Отдельное слагаемое S_i; равно площади прямоугольника со сторонами ∆x и f(x), где i = 1, 2,..., n. Метод прямоугольников является простейшим, но и наименее точным. Более точно определенный интеграл может быть вычислен по формуле трапеций . В этом случае, в отличие от метода прямоугольников, на каждом из отрезков разбиения [x_i-1, x_i] участок кривой y=f(x) заменяется хордами, стягивающими концевые точки. Тогда, отдельное слагаемое интегральной суммы S_i, равно площади трапеции с основаниями f(x_i) и f(x_i-1) и высотой Ах, где i = 1, 2,..., n, то есть:

Складывая площади элементарных трапеций и приводя подобные члены, получаем формулу (5). Погрешность ∆ вычисления определенного интеграла по формуле трапеций S(n):

может быть оценена из выражения:

,

где М₂ - максимальное значение модуля второй производной f"(x) подынтегральной функции y=f(х) на [a, b].

Рассмотрим пример вычисления интегралов по методу прямоугольников и методу трапеций. Пусть требуется вычислить интеграл с шагом ∆х=0,1:

Аналитически данный интеграл может быть вычислен просто:

.

Метод прямоугольников. Для нахождения определенного интеграла данным методом необходимо ввести значения подынтегральной функции f(x) в рабочую таблицу Excel в диапазоне х[0; 3] с заданным шагом ∆ x=0,1.

1. Составляем таблицу данных х и f(х). Пусть столбец А будет хранить значения х, а второй столбец В – значения функции f(x). Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 - слово Функция, в ячейку А2 вводится первое значение аргумента - левая граница диапазона (0), а в ячейку A3 вводится второе значение аргумента - левая граница диапазона плюс шаг построения (0,1). Затем, выделив ячейки А2:АЗ, автозаполнением формируем все значения аргумента (за правый нижний угол блока А2:А3 курсор протягиваем до ячейки А32, до значения х=3).

2. Затем вводим значения подынтегральной функции, в ячейку В2 необходимо записать ее уравнение. Для этого табличный курсор необходимо установить в ячейку В2, ввести формулу =А2^2 и нажимаем Enter. В ячейке В2 появляется 0. Далее необходимо автозаполнением скопировать функцию из ячейки В2 в диапазон В2:В32 и в результате должна быть получена таблица данных для нахождения интеграла.

3. Теперь в ячейке ВЗЗ может быть найдено приближенное значение интеграла, для чего в ячейку ВЗЗ вводим формулу =0,1*, затем вызываем Мастер функций. В поле Функция выбираем функцию Сумм и нажимаем кнопку ОК. В рабочее поле диалогового окна СУММ мышью определяем диапазон суммирования ВЗ:В32, заполняя поле Число1 и нажимаем кнопку ОК. В ячейке ВЗЗ появляется приближенное значение искомого интеграла (9,455). На рис.4.46. приведен фрагмент таблицы для вычисления интеграла.

Рис.4.46.Вычисление интеграла

Сравнивая полученное значение с истинным значением вычисления интеграла - 9 можно отметить, что ошибка метода прямоугольников довольно значительна - 0,455.

Метод трапеций. Для нахождения определенного интеграла методом трапеций, как и в случае использования метода прямоугольников, значения подынтегральной функции f(х) должны быть введены в рабочую таблицу в диапазоне х [0; 3) с заданным шагом ∆ х=0,1. Поэтому этапы 1-3 полностью аналогичны этапам предыдущего решения. Поскольку таблица данных для нахождения интеграла уже введена, обсудим только этап 3. В ячейке В34 нужно вычислить приближенное значение интеграла по методу трапеций. Для этого в ячейку В34 вводим формулу =0,1*((В2 + В32)/2, затем вызываем Мастер функций. В рабочем поле диалогового окна Сумм определяем диапазон суммирования ВЗ:В31 и нажимаем кнопку ОК. В результате в ячейке В34 формируется приближенное значение искомого интеграла (9,005). Сравнивая полученное значение интеграла с истинным, можно отметить, что ошибка вычисления методом трапеций является вполне приемлемой - 0,005.