Порядок выполнения работы

Для решения задач по вычислению показателей эффективности инвестиций используем тот же алгоритм работы и финансовые функции, что и для денежных потоков.

В таких задачах рассматривается поток платежей, совершаемых через одинаковые промежутки времени, но сами выплаты могут различаться и по величине, и по знаку. В качестве исходных данных – поток платежей и процентная ставка, необходимо вычислить – современное значение суммы платежей, т.е. привести все платежи к начальному моменту времени, и вычислить эффективную процентную ставку операции.

Для этого предназначены две функции ЧПС {НПЗ} – чистое (нетто) приведенное значение (NPV – net present value) и ВСД {ВНДОХ} – внутренняя ставка доходности (IRR – internal rate of return).

ЧПС {НПЗ} – возвращает величину чистой приведенной стоимости инвестиции, основанной на серии периодических денежных потоков, используя ставку дисконтирования, а также стоимости будущих выплат (отрицательные значения) и поступлений (положительные значения). Синтаксис функции – ЧПС (ставка; значение 1; значение 2;...):

Ставка – ставка дисконтирования за один период.

Значение 1, значение 2,... (выплаты) – от 1 до 29 аргументов, представляющих расходы и доходы. Значение 1, значение 2,... должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.

ЧПС использует порядок аргументов значение 1, значение 2,... для определения порядка поступлений и платежей. Необходимо убедиться в том, что платежи и поступления введены в функцию в правильном порядке.

Функция по умолчанию учитывает аргументы, которые являются числами, пустыми ячейками, логическими значениями или текстовыми представлениями чисел. Аргументы, которые являются значениями ошибки или текстами, которые не могут быть преобразованы в числа, игнорируются. Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст или значения ошибок в массиве или ссылке также игнорируются.

Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за один период до даты денежного взноса значение1 и заканчивается с последним денежным взносом в списке. Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение не включается в список аргументов функции, а добавляется к результату функции ЧПС.

Если n — это количество денежных потоков в списке значений, то формула для функции ЧПС имеет вид:

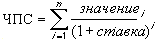
Очевидно, что ЧПС аналогична функции ПС (приведенная стоимость). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В отличие от денежных взносов переменной величины в функции ЧПС, денежные взносы в функции ПС должны быть постоянны на весь период инвестиции. Для получения информации о функциях платежей по ссуде и финансовых функциях см. Тему 3.

ЧПС также связана с функцией ВСД (внутренняя ставка доходности). ВСД – это ставка, для которой ЧПС равняется нулю: ЧПС(ВСД(...);...) = 0.

Внутренняя ставка доходности – это процентная ставка, принимаемая для инвестиции, состоящей из платежей (отрицательные величины) и доходов (положительные величины), которые осуществляются в последовательные и одинаковые по продолжительности периоды.

ВСД {ВНДОХ} – возвращает внутреннюю ставку доходности (отдачи) для ряда потоков денежных средств, представленных их численными значениями. Эти денежные потоки не обязательно должны быть равными по величине, как в случае аннуитета. Однако они должны иметь место через равные промежутки времени, например, ежемесячно или ежегодно. Синтаксис функции – ВСД (значения; предположение):

Значения (выплаты) – это массив или ссылка на ячейки, содержащие числа, для которых требуется подсчитать внутреннюю ставку доходности. Значения должны содержать, по крайней мере, одно положительное и одно отрицательное значение. ВСД использует порядок значений для интерпретации порядка денежных выплат или поступлений. Значения выплат и поступлений должны быть введены в правильном порядке. Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения игнорируются.

Предположение (начальное_приближение) – это величина, о которой предполагается, что она близка к результату ВСД. Excel использует метод итераций для вычисления ВСД. Начиная со значения предположение, функция ВСД выполняет циклические вычисления, пока не получит результат с точностью 0,00001 процента. Если функция ВСД не может получить результат после 20 попыток, то выдается значение ошибки #ЧИСЛО!. В большинстве случаев нет необходимости задавать предположение для вычислений с помощью функции ВСД. Если предположение опущено, то оно полагается равным 0,1 (10 процентов).

Если ВСД возвращает значение ошибки #ЧИСЛО! или если результат далек от ожидаемого, можно попытаться выполнить вычисления еще раз с другим значением аргумента предположение.

Функция ВСД тесно связана с функцией ЧПС. Ставка доходности, вычисляемая ВСД, связана с нулевой чистой текущей стоимостью. Взаимосвязь функций ЧПС и ВСД отражена в следующей формуле:

ЧПС(ВСД(B1:B6);B1:B6) равняется 3.60E-08. Учитывая точность расчета для функции ВСД, значение 3,60E-08 можно считать 0 (нулевым).

Задачи

12. Проект рассчитан на три года и требует начальных инвестиций в размере 10 млн. руб. и имеет предполагаемые денежные поступления в размере 3 млн. руб., 4 млн. руб., 7 млн. руб. Рассчитать NPV в предположении ставки 10% и определить IRR для этого проекта.

Указание. Рассчитать NPV без функции ЧПС и проверить полученный результат с помощью функции ЧПС. Следует обратить внимание, что начальная выплата в аргумент функции ЧПС не включается, а добавляется как отдельное слагаемое. Функция ВСД, вычисляющая внутреннюю норму доходности, напротив, использует начальную выплату.

Для того чтобы лучше понять взаимоотношение NPV и IRR, построить отдельную таблицу значений NPV для различных процентных ставок от 0% до 20% с шагом 2,5%. На основе данных таблицы построить график вида

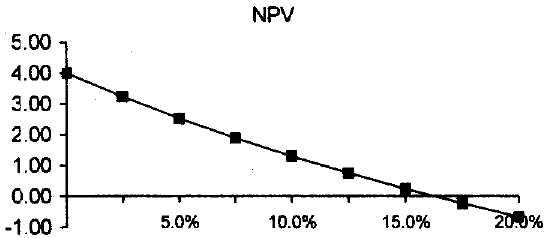
По графику определить, при каких значениях NPV проект принимается, а при каких – отклоняется.

13. Предлагаются два инвестиционных проекта, которые характеризуются предполагаемыми потоками платежей:

Год	Проект А	Проект В
0	-100	-100
1	50	20
2	40	40
3	40	50
4	30	60
Сумма	60	70

Сравнить проекты на основе NPV и IRR.

Указание. Построить столбиковую диаграмму для потоков платежей. Проанализировать по виду диаграммы, какой проект эффективнее.

Проверить выводы путем расчета IRR. Определить, какой проект предпочтительнее.

Рассчитать NPV, составив таблицу зависимости NPV от r для обоих проектов (процентная ставка изменяется от 0% до 30% с шагом 2,5%), построить линейные графики для обоих проектов на одном поле.

Определить по диаграмме, при какой ставке пересекаются графики. Более точное значение подобрать с помощью команды «Сервис/Подбор параметра» Сделать вывод, при какой ставке выгоднее проект А, а при какой – выгоднее проект В.

14. Контракт между фирмой А и банком В предусматривает, что банк предоставляет в течение трех лет кредит фирме ежегодными платежами в размере 1 млн. долл. в начале каждого года под ставку 10% годовых. Фирма возвращает долг, выплачивая 1, 2 и 1 млн. долл. последовательно в конце 3-го, 4-го и 5-го годов. Выгодна ли эта операция банку? Какой доход получит банк?

Указание. Выгодность операции для банка можно определить, сравнив IRR с установленной процентной ставкой.