§9. Задачи для самостоятельной работы

I. Упростить граф.

1)	2)
3)	4)
5)	6)

II. По данной системе уравнений построить нормализованный граф, считая указанную переменную источником. По графу составить нормализованную матрицу и соответствующую систему уравнений.

1) ,– источник.	2) ,– источник.
3) ,– источник.	4) ,– источник.
5) ,– источник.	6) ,–источник.

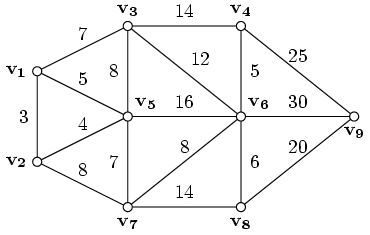
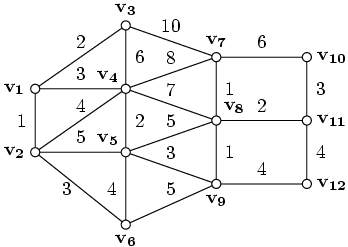
III. С помощью алгоритма Дейкстры найти расстояние от вершины v₁ до остальных вершин и построить покрывающее дерево кратчайших путей.

1)
2)
3)
4)
5)
6)

IV. Для проектов, заданных приведенными ниже сетевыми графиками, найти критическое время, и, считая Т=, найти ранние и поздние сроки начала и окончания работ, а также полные и свободные резервы времени.

1)
2)
3)
4)

Литература

1. Елемичев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. – М.: «Наука», Гл. ред. физ.-мат. лит., 1990.

2. Справочник по математике для экономистов. / Под ред. проф. В.И. Ермакова. – М.: «Высшая школа», 1987.

3. Зыков А.А. Основы теории графов. – М.: «Наука», 1987.

4. Татт У. Теория графов. – М.: «Мир», 1988.

5. В.А. Горбатов. Основы дискретной математики: Учебное пособие для вузов. – М.: «Высшая школа», 1986.

6. Р.Басакер, Т.Саати. Конечные графы и сети. – М.: «Наука», Гл. ред. физ.-мат. лит., 1974.

7. Яблонский С.В. Введение в дискретную математику. – М.: «Наука», 1986.

Пирозерский Алексей Леонидович

Пирозерская Людмила Павловна

Математика. Основы дискретной математики Методические указания по изучению курса

	Подп. к печати 14.05.2004	Формат 6084 1/16
Усл. печ. л. 0,97	Уч.-изд. л. 2,5	Тираж 500 экз.
Изд. № 001	Заказ №0357

РИО СПбГАСЭ, лицензия ЛР № 040849

Член Издательско-полиграфической Ассоциации университетов России

СПб государственная академия сервиса и экономики

193171, Г. Санкт-Петербург, ул. Седова, 55/1

Отпечатано в ИИГ НОУ «АКТиБ», 193171, СПб., ул. Седова, 55/1

Лицензия ИД №05598 от 14.08.2001 г.

43