§4. Уравнения и графы

Рассмотрим систему, состоящую из нескольких узлов, каждому из которых соответствует некоторый узловой сигнал (воздействие) . Узлы связаны направленными линиями, по которым они могут принимать или передавать сигналы другим узлам. Каждая линия характеризуется величиной, которая называетсяпередачей, и определяется как отношение сигнала на выходе линии к сигналу на ее входе. Узел называется зависимым, если имеет одну или несколько входящих линий. Узловой сигнал предполагается равным сумме входных сигналов. Наличие выходящих линий из узла не влияет на сигнал этого узла(они влияют на сигналы других узлов).

Такую систему можно представить в виде некоторого орграфа (сети), в котором узлам системы соответствуют вершины, линиям связи – дуги, направление которых соответствует направлению передачи сигнала. Вершины удобно обозначать их узловыми сигналами , дуги – парами чисел , где– номер узла, из которого выходит данная линия,– в который входит. Передача дугиобозначается. Например:

Первому из этих орграфов соответствует простейшее уравнение , второму – система уравнений

Рассмотрим систему трех уравнений:

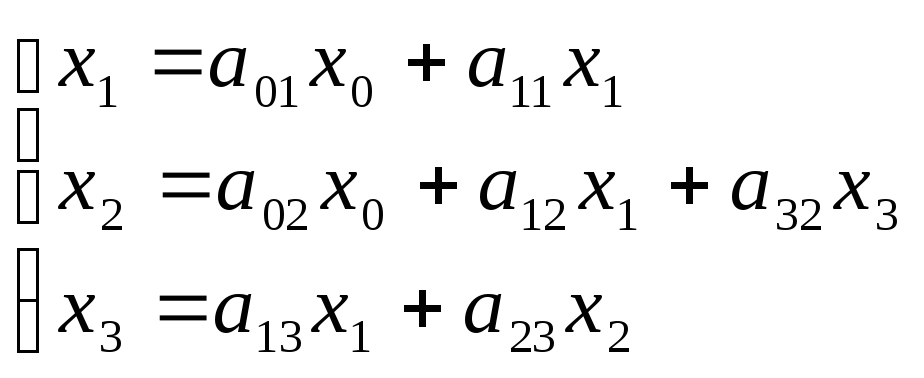
Ее граф имеет вид:

Здесь два контура обратной связи: петля и цикл (,).

Существует три типа вершин:

1. источники – вершины, которые имеют только выходящие дуги;

2. простые каскадные узлы – имеют как выходящие, так и входящие дуги;

3. стоки – вершины, имеющие только входящие дуги.

Источники соответствуют независимым переменным, а стоки - зависимым. Графы, не содержащие контуров обратной связи, называются каскадными графами.

Например, рассмотрим граф, показанный на рис. 4:

Рис. 4.

Рис. 5.

Он выражает следующие уравнения: .

Так как имеются лишь один источник и один сток, которые связаны только прямыми путями (т.е. такими, вдоль которых номера вершин возрастают), то можно построить простой граф, задающий как функцию. Такой упрощенный граф (см. рис. 5) называетсяприведенным относительно исходного графа.

Искомую передачу легко определить, выразив в уравнениях ичерез:, откуда.

§5. Правила упрощения орграфов для систем уравнений

Исключению зависимых переменных из системы уравнений соответствуют преобразования орграфов, позволяющие заменить последовательные и параллельные пути отдельными ветвями и, таким образом, упростить орграф.

Рассмотрим основные правила упрощения орграфов.

1. Передача последовательно соединенных рёбер равна произведению передач этих рёбер (рис.6). Действительно, ,, откуда.

2. Передача двух параллельных одинаково направленных рёбер равна сумме передач этих рёбер (рис.7).

   	=>			=>
   Рис. 6.			Рис. 7.

3. Устранение простой вершины (не входящей в контур обратной связи).

Рис. 8.	Рис. 9.

Действительно, ,, откуда(рис. 8). Аналогично, для рис. 9, находим:,,, откуда,.

4. Устранение контура на пути (рис. 10).

Имеем: ,, следовательно,.

Рис. 10.	Рис. 11.

5. Исключение петли, когда к узлу подходит и из него отходит по одной ветви (рис. 11).

Очевидно, ,. Из первого равенства, тогда(предполагается, что).

6. Исключение петли, когда к узлу подходят и из него выходят несколько рёбер.

В этом случае вводится дополнительная вершина, к которому подходят те же ветви, которые подходили к узлу с петлей.

Для первого графа: или, откуда

и . Для второго графа:,,и

. Таким образом, при исключении петли передачи всех входящих рёбер умножаются на , а исходящие ветви остаются без изменения.

7. Замена двух и большего числа петель одной петлей.

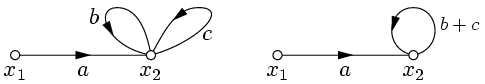
8. Удлинение (растяжение) вершину.

В некоторых случаях при преобразованиях графов оказывается полезным «удлинить» вершину. Пусть, например, надо удлинить вершину 2 графа, приведенного на рис. 12:

Рис. 12.	Рис. 13.

Для этого:

1) вершину 2 подразделяют на две: на старую вершину 2, от которой отходят те же ветви, что и в первоначальном графе, и на новую вершину , к которому подходят те же ветви, что подходили к вершине 2 в исходном графе;

2) узлы 2 и соединяют ребром, передача которого равна 1.

В результате получим граф, изображенный на рис. 13. Справедливость преобразования проверить самостоятельно.

9. Инверсия пути.

Рассмотрим уравнение: . Соответствующий ему граф показан на рис. 14. Здесь– зависимая переменная. Можно разрешить это уравнение относительно переменнойили. Например,. Ему соответствует граф (см. рис. 15), в котором осуществленаинверсия пути по сравнению с исходным графом.

Рис. 14.	Рис. 15.

Рассмотрим несколько примеров.

Пример 1. Построить граф по заданной системе уравнений 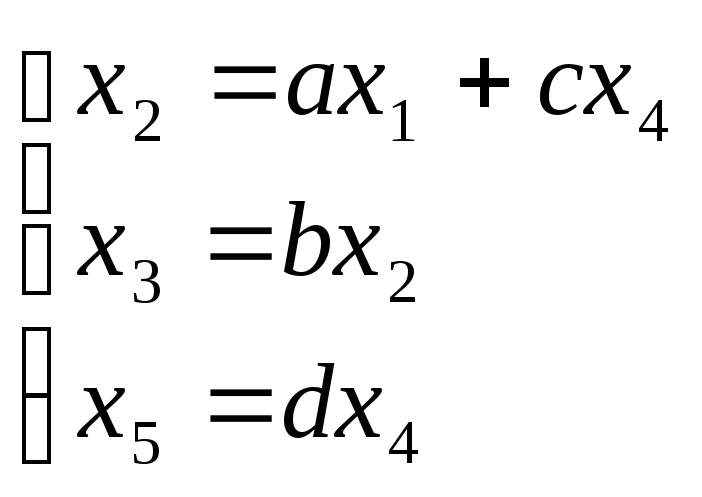; исключить вершину и написать соответствующую систему уравнений.

Данной системе уравнений соответствует граф, показанный на рис. 16.

Рис. 16.	Рис. 17.

После исключения узла получим граф, изображенный на рис. 17. Ему соответствует система уравнений.

Пример 2. Исключить петлю и упростить граф, изображенный на рис. 18.

Рис. 18.	Рис. 19.

Сначала исключим петлю, применив правило 5 (рис. 19). Затем, в соответствии с правилом 1, исключим x₃ (рис. 20) и применим правило 2 (рис. 21).

Рис. 20.	Рис. 21.

Таким образом, .

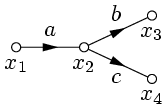
Пример 3. Исключить петлю и упростить граф, изображенный на рисунке:

Применим правило 1 (рис. 22), затем правила 5 и 1 (рис. 23).

Рис. 22.	Рис. 23.

Таким образом, .

Пример 4. Упростить граф, изображенный на рисунке:

Первый способ:		Второй способ:
Окончательно получим:			.

Пример 5. Упростить граф, изображенный на рисунке:

Последовательные преобразования графа показаны на рис. 24 – рис. 26.

Рис. 24.	Рис. 25.

	.
Рис. 26.

Пример 6. Дана система уравнений . Построить ее полный граф и упрощенный граф, в котором переменнаявыражена через.

Полный граф системы показан на рис. 27. Преобразовав его, получим упрощенный граф (рис. 28).

Рис. 27.	Рис. 28.

Таким образом, .